1.1.1 集合的含义与表示 (集合的表示) 第2课时 课件(共21张PPT)
文档属性
| 名称 | 1.1.1 集合的含义与表示 (集合的表示) 第2课时 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-07 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
人教版 初中数学
第2课时 集合的表示
表示一个集合具体有哪些方法呢?
这一节课我们就来研究!
新课导入
集合的表示方法
把集合的元素_________出来,并用花括号“{ }” 括起来表示集合的方法叫做列举法.
1.列举法:
元素
无序
互异
一一列举
课堂探究
注意:
元素间要用逗号隔开.
例如:A={9,8,7,6,5,4,3,2,1,0}
例1 用列举法表示下列集合:
(1)小于10的所有自然数组成的集合.
(2)方程x2=x的所有实数根组成的集合.
(3)由1~20以内的所有素数组成的集合.
解:(1)设小于10的所有自然数组成的集合为A,那么A={0,1,2,3,4,5,6,7,8,9}.
(2)设方程x2=x的所有实数根组成的集合为B,那么B={1,0}.
(3)设由1~20以内的所有素数组成的集合为C,那么C={2,3,5,7,11,13,17,19}.
【提升总结】由于元素完全相同的两个集合相等,而与列举的顺序无关,因此集合可以有不同的列举方法.例如,
例1(1)可以表示为A={9,8,7,6,5,4,3,2,1,0}
用列举法表示下列集合
(1)小于5的所有正整数组成的集合
(2) 函数y=x+1与y=- x+1的图象的交点组成的集合
(3)不等式x-3<7的解集
思考:是否所有集合都能用列举法来表示?
否,集合中的元素个数是有限的,即有限集可以用.
变式训练
为无限集,无法用列举法表示.
{1,2,3,4}
{(1,2)}
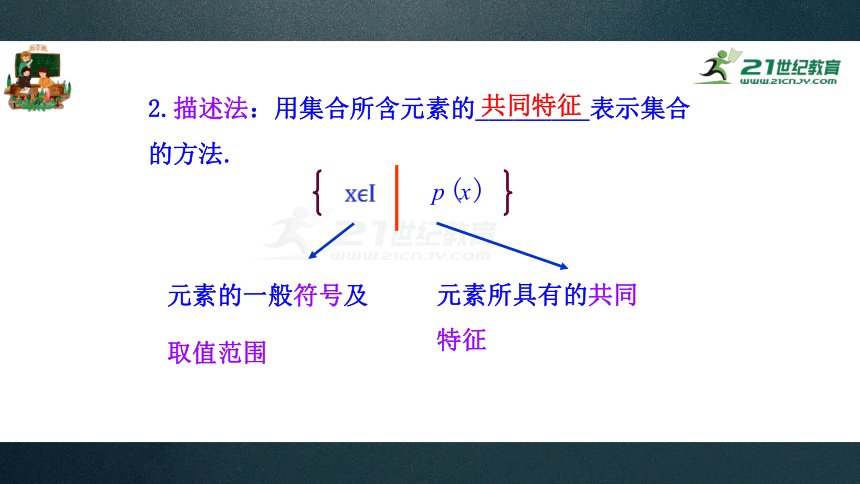
2.描述法:用集合所含元素的_________表示集合
的方法.
元素的一般符号及取值范围
元素所具有的共同特征
共同特征
【想一想】
1. a与{a}的含义是否相同?
不同,前者为元素,后者为集合.
2. 集合{y|y=x2,x∈R}与集合{x|y=x2, x∈R}相同吗?
不同,前者是函数的所有函数值组成的集合;
后者是函数的所有自变量组成的集合.
例2 试分别用列举法和描述法表示下列集合.
(1)方程x2-2=0的所有实数根组成的集合.
(2)由大于10小于20的所有整数组成的集合.
方程x2-2=0有两个实数根为 ,因此,用列举法表示为A={ }.
解:(1)设方程x2-2=0的实数根为x,并且满足条件
x2-2=0,因此,用描述法表示为A={x∈R|x2-2=0}.
大于10小于20的整数有11,12,13,14,15,16,17, 18,19,因此,用列举法表示为
B={x∈Z∣10B={11,12,13,14,15,16,17,18,19}.
(2)设大于10小于20的整数为x,它满足条件x∈Z,且10注意:描述法关键是要抓住集合中元素的共同特征,一般用符号语言来表示;而其条件所描述的对象即代表元素要写到竖线的前面.
变式训练
用给定的方法表示集合:
(1)用列举法表示集合A={x|x2-3x+2=0};
(2)用描述法表示“比-2大,且比1小的所有实数”组成的集合B;
(3)用另一种方法表示集合
C={(x,y)|x+y=5,x∈N,y∈N}。
解:(1)A={1,2};
(2)B={x|-2<x<1};
(3)C={(0,5),(1,4),(2,3),(3,2),(4,1),(5,0)}。
自然语言 列举法 描述法
特点
适用对象
容易理解
直观明了
元素有共同的特征
所有
元素不太多的集合
元素无限或很多的集合
表示方法的特点以及使用对象
课后小结
1.集合{x∈N+|x-2<4}用列举法可表示为( )
A.{0,1,2,3,4} B.{1,2,3,4}
C.{0,1,2,3,4,5} D.{1,2,3,4,5}
解析:{x∈N+|x-2<4}={x∈N+|x<6}={1,2,3,4,5}.
答案:D
课后练习
2.集合{(x,y)|y=2x+3}表示( )
A.方程y=2x+3
B.点(x,y)
C.函数y=2x+3图象上的所有点组成的集合
D.平面直角坐标系中的所有点组成的集合
解析:集合{(x,y)|y=2x+3}的代表元素是(x,y),x,y满足的关系式为y=2x+3,因此集合表示的是满足关系式y=2x-1的点组成的集合.
答案:C
3.已知集合A={x∈N|-≤x≤},则有( )
A.-1∈A B.0∈A C.∈A D.2∈A
解析:因为0是整数且满足-≤x≤,所以0∈A.
答案:B
4.由大于-3且小于11的偶数组成的集合是( )
A.{x|-3B.{x|-3C.{x|-3D.{x|-3
解析:{x|x=2k,k∈Z}表示所有偶数组成的集合.
由-3答案:D
5.由a2,2-a,4组成一个集合A,A中含有3个元素,则实数a的取值可以是( )
A.1 B.-2 C.6 D.2
解析:因A中含有3个元素,即a2,2-a,4互不相等,将选项中的数值代入验证可知答案选C.
答案:C
6.用适当的方法表示下列给定的集合.
(1)比4大2的数.
(2)所有奇数组成的集合.
(3)大于1且小于6的整数.
陶行知的名言
行是知之始,知是行之成。
https://www.21cnjy.com/help/help_extract.php
人教版 初中数学
第2课时 集合的表示
表示一个集合具体有哪些方法呢?
这一节课我们就来研究!
新课导入
集合的表示方法
把集合的元素_________出来,并用花括号“{ }” 括起来表示集合的方法叫做列举法.
1.列举法:
元素
无序
互异
一一列举
课堂探究
注意:
元素间要用逗号隔开.
例如:A={9,8,7,6,5,4,3,2,1,0}
例1 用列举法表示下列集合:
(1)小于10的所有自然数组成的集合.
(2)方程x2=x的所有实数根组成的集合.
(3)由1~20以内的所有素数组成的集合.
解:(1)设小于10的所有自然数组成的集合为A,那么A={0,1,2,3,4,5,6,7,8,9}.
(2)设方程x2=x的所有实数根组成的集合为B,那么B={1,0}.
(3)设由1~20以内的所有素数组成的集合为C,那么C={2,3,5,7,11,13,17,19}.
【提升总结】由于元素完全相同的两个集合相等,而与列举的顺序无关,因此集合可以有不同的列举方法.例如,
例1(1)可以表示为A={9,8,7,6,5,4,3,2,1,0}
用列举法表示下列集合
(1)小于5的所有正整数组成的集合
(2) 函数y=x+1与y=- x+1的图象的交点组成的集合
(3)不等式x-3<7的解集
思考:是否所有集合都能用列举法来表示?
否,集合中的元素个数是有限的,即有限集可以用.
变式训练
为无限集,无法用列举法表示.
{1,2,3,4}
{(1,2)}
2.描述法:用集合所含元素的_________表示集合
的方法.
元素的一般符号及取值范围
元素所具有的共同特征
共同特征
【想一想】
1. a与{a}的含义是否相同?
不同,前者为元素,后者为集合.
2. 集合{y|y=x2,x∈R}与集合{x|y=x2, x∈R}相同吗?
不同,前者是函数的所有函数值组成的集合;
后者是函数的所有自变量组成的集合.
例2 试分别用列举法和描述法表示下列集合.
(1)方程x2-2=0的所有实数根组成的集合.
(2)由大于10小于20的所有整数组成的集合.
方程x2-2=0有两个实数根为 ,因此,用列举法表示为A={ }.
解:(1)设方程x2-2=0的实数根为x,并且满足条件
x2-2=0,因此,用描述法表示为A={x∈R|x2-2=0}.
大于10小于20的整数有11,12,13,14,15,16,17, 18,19,因此,用列举法表示为
B={x∈Z∣10
(2)设大于10小于20的整数为x,它满足条件x∈Z,且10
变式训练
用给定的方法表示集合:
(1)用列举法表示集合A={x|x2-3x+2=0};
(2)用描述法表示“比-2大,且比1小的所有实数”组成的集合B;
(3)用另一种方法表示集合
C={(x,y)|x+y=5,x∈N,y∈N}。
解:(1)A={1,2};
(2)B={x|-2<x<1};
(3)C={(0,5),(1,4),(2,3),(3,2),(4,1),(5,0)}。
自然语言 列举法 描述法
特点
适用对象
容易理解
直观明了
元素有共同的特征
所有
元素不太多的集合
元素无限或很多的集合
表示方法的特点以及使用对象
课后小结
1.集合{x∈N+|x-2<4}用列举法可表示为( )
A.{0,1,2,3,4} B.{1,2,3,4}
C.{0,1,2,3,4,5} D.{1,2,3,4,5}
解析:{x∈N+|x-2<4}={x∈N+|x<6}={1,2,3,4,5}.
答案:D
课后练习
2.集合{(x,y)|y=2x+3}表示( )
A.方程y=2x+3
B.点(x,y)
C.函数y=2x+3图象上的所有点组成的集合
D.平面直角坐标系中的所有点组成的集合
解析:集合{(x,y)|y=2x+3}的代表元素是(x,y),x,y满足的关系式为y=2x+3,因此集合表示的是满足关系式y=2x-1的点组成的集合.
答案:C
3.已知集合A={x∈N|-≤x≤},则有( )
A.-1∈A B.0∈A C.∈A D.2∈A
解析:因为0是整数且满足-≤x≤,所以0∈A.
答案:B
4.由大于-3且小于11的偶数组成的集合是( )
A.{x|-3
解析:{x|x=2k,k∈Z}表示所有偶数组成的集合.
由-3
5.由a2,2-a,4组成一个集合A,A中含有3个元素,则实数a的取值可以是( )
A.1 B.-2 C.6 D.2
解析:因A中含有3个元素,即a2,2-a,4互不相等,将选项中的数值代入验证可知答案选C.
答案:C
6.用适当的方法表示下列给定的集合.
(1)比4大2的数.
(2)所有奇数组成的集合.
(3)大于1且小于6的整数.
陶行知的名言
行是知之始,知是行之成。
https://www.21cnjy.com/help/help_extract.php
