人教版数学七年级下册:5.4-平移 同步练习(含答案)
文档属性
| 名称 | 人教版数学七年级下册:5.4-平移 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 315.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-03 07:36:36 | ||
图片预览



文档简介
平移 同步练习
一.选择题(共12小题)
1.下列现象中是平移的是( )
A.将一张纸沿它的中线折叠 B.电梯的上下移动
C.飞碟的快速转动 D.翻开书中的每一页纸张
2.如图,直线L1是由直线L2平移得到的,若∠1=56°,则∠2的度数为( )
A.∠2=56°
B.∠2=124°
C.∠2=134°
D.∠2=114°
3.第七届世界军人运动会(7thCISMMilitaryWorldGames),于2019年10月18日至27日在中国武汉举行,图中是吉祥物“兵兵”,将图中的“兵兵”通过平移可得到图为( )
4.如图是6级台阶侧面示意图,如果要在台阶上铺红地毯,那么地毯长度至少需要( )
A.8米
B.5米
C.4米
D.3米
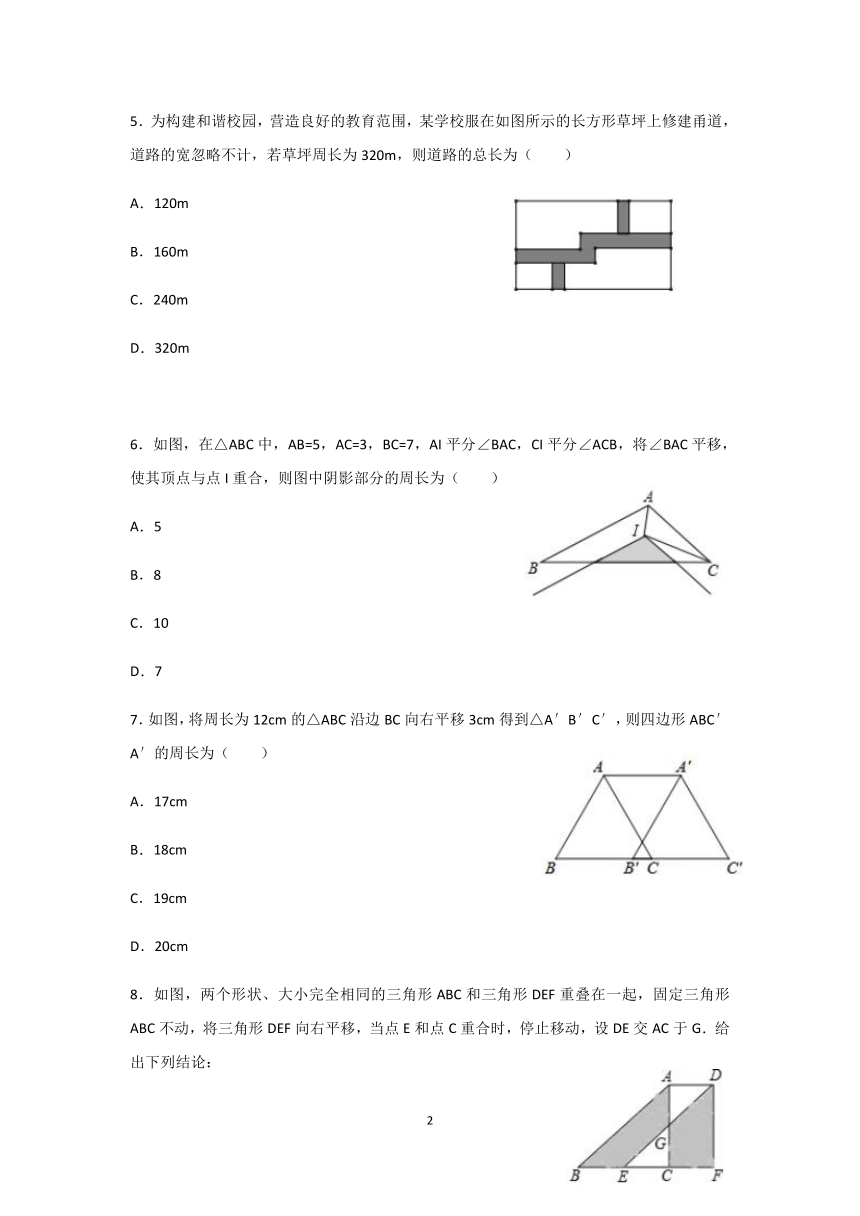
5.为构建和谐校园,营造良好的教育范围,某学校服在如图所示的长方形草坪上修建甬道,道路的宽忽略不计,若草坪周长为320m,则道路的总长为( )
A.120m
B.160m
C.240m
D.320m
6.如图,在△ABC中,AB=5,AC=3,BC=7,AI平分∠BAC,CI平分∠ACB,将∠BAC平移,使其顶点与点I重合,则图中阴影部分的周长为( )
A.5
B.8
C.10
D.7
7.如图,将周长为12cm的△ABC沿边BC向右平移3cm得到△A′B′C′,则四边形ABC′A′的周长为( )
A.17cm
B.18cm
C.19cm
D.20cm
8.如图,两个形状、大小完全相同的三角形ABC和三角形DEF重叠在一起,固定三角形ABC不动,将三角形DEF向右平移,当点E和点C重合时,停止移动,设DE交AC于G.给出下列结论:
①四边形ABEG的面积与CGDF的面积相等;
②AD∥EC,且AD=EC,
则( )
A.①,②都正确
B.①正确,②错误
C.①,②都错误
D.①错误,②正确
9.如图,表示直线a平移得到直线b的两种画法,下列关于三角板平移的方向和移动的距离说法正确的是( )
A.方向相同,距离相同
B.方向不同,距离不同
C.方向相同,距离不同
D.方向不同,距离相同
10.如图,将△ABC沿着某一方向平移一定的距离得到△DEF,则下列结论:
①AD=CF;②AC∥DF;③∠ABC=∠DFE;④∠DAE=∠AEB.
正确的个数为( )
A.4个
B.3个
C.2个
D.1个
11.如图,两个直角三角形重叠在一起,将其中一个沿点B到点C的方向平移到△DEF的位置,AB=10,DH=4,BC=15,平移距离为6,则阴影部分的面积( )
A.40
B.42
C.45
D.48
12.如图,有两条长分别为a、b的铁丝,其中长为a的铁丝恰好围成一个大正方形;AB是大正方形的对角线,把AB分成n条相等的线段,再以每条线段作为小正方形的对角线,长为b的铁丝恰好能围成n个这样的小正方形;若均不考虑接口情况,则a、b的大小关系是( )
A.a>b
B.a<b
C.a=b
D.a≥b
二.填空题(共5小题)
13.如图,将周长为18cm的△ABC沿BC平移1cm得到△DEF.则AD= cm.
14.如图,某小区规划在长,宽分别为4x,3x的长方形场地上,修建三条互相垂直且宽均为y米的甬道(单位:m),其余阴影部分种草,则阴影部分的面积为 (用含x、y的式子表示,并计算出最终结果.)
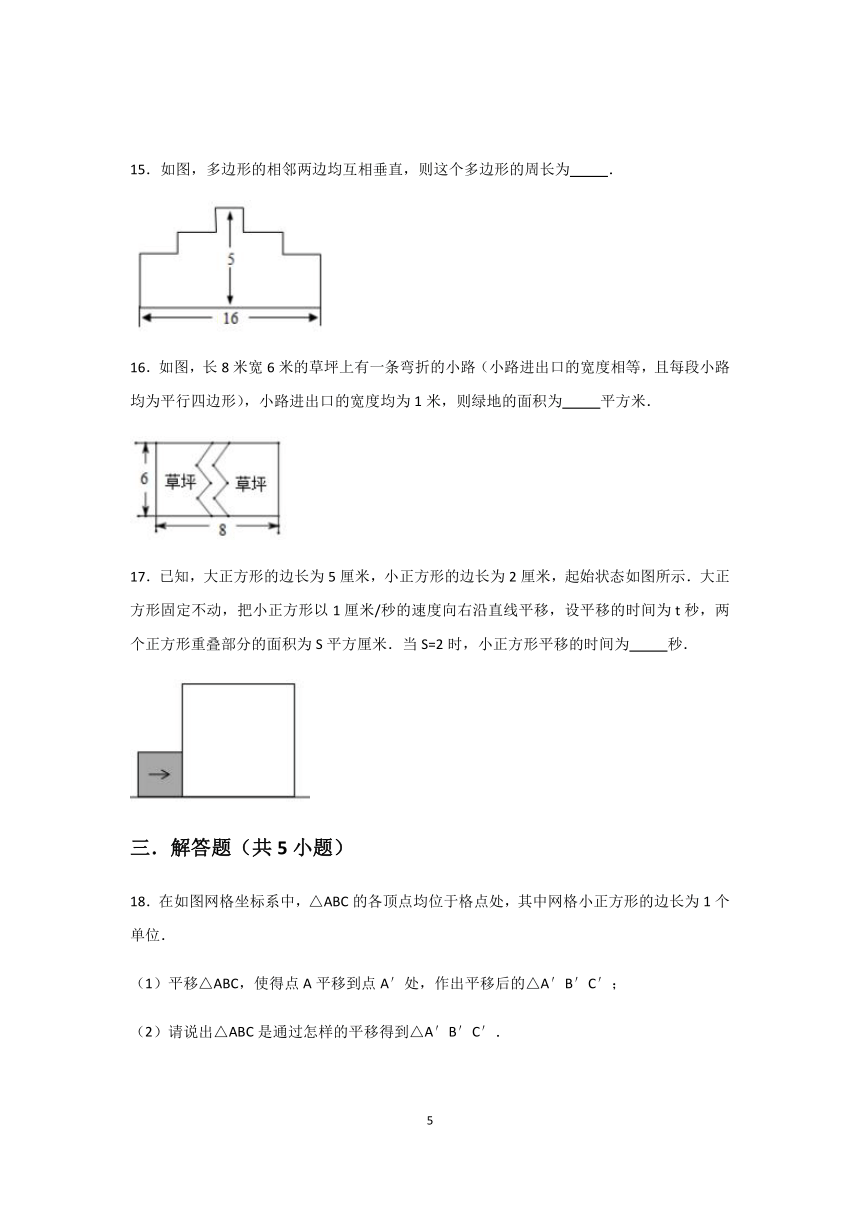
15.如图,多边形的相邻两边均互相垂直,则这个多边形的周长为 .
16.如图,长8米宽6米的草坪上有一条弯折的小路(小路进出口的宽度相等,且每段小路均为平行四边形),小路进出口的宽度均为1米,则绿地的面积为 平方米.
17.已知,大正方形的边长为5厘米,小正方形的边长为2厘米,起始状态如图所示.大正方形固定不动,把小正方形以1厘米/秒的速度向右沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S平方厘米.当S=2时,小正方形平移的时间为 秒.
三.解答题(共5小题)
18.在如图网格坐标系中,△ABC的各顶点均位于格点处,其中网格小正方形的边长为1个单位.
(1)平移△ABC,使得点A平移到点A′处,作出平移后的△A′B′C′;
(2)请说出△ABC是通过怎样的平移得到△A′B′C′.
19.如图,已知△ABC在平面直角坐标系中的位置如图所示,
(1)写出△ABC三个顶点的坐标;
(2)求出△ABC的面积;
(3)在图中画出把△ABC先向左平移5个单位,再向上平移2个单位后所得的△A′B′C′,并写出各顶点坐标.
20.操作与探究:对数轴上的任意一点P.
①作出点N使得N和P表示的数互为相反数,再把N对应的点向右平移1个单位,得到点P的对应点P′.我们称P′是P的N变换点;
②把P点向右平移1个单位,得到点M,作出点P′′使得P′′和M表示的数互为相反数,我们称P′′是P的M变换点.
(1)如图,若点P表示的数是-4,则P的N变换点P′表示的数是 ;
(2)若P的M变换点P′′表示的数是2,则点P表示的数是 ;
(3)若P′,P′′分别为P的N变换点和M变换点,且OP′=2OP′′,求点P表示的数.
21.如图,一块边长为8米的正方形土地,在上面修了三条道路,宽都是1米,空白的部分种上各种花草.
(1)请利用平移的知识求出种花草的面积.
(2)若空白的部分种植花草共花费了4620元,则每平方米种植花草的费用是多少元?
(3)如图,一块边长为a米的正方形土地,在上面修了3条道路,宽都是b米,空白的部分种上各种花草,则求出种花草的面积.
22.(1)如图1,已知MN∥PQ,B在MN上,D在PQ上,点E在两平行线之间,求证:∠BED=∠PDE+∠MBE;
(2)如图2,已知MN∥PQ,B在MN上,C在PQ上,A在B的左侧,D在C的右侧,DE平分∠ADC,BE平分∠ABC,直线DE、BE交于点E,∠CBN=100°.
①若∠ADQ=130°,求∠BED的度数;
②将线段AD沿DC方向平移,使得点D在点C的左侧,其他条件不变,如图3所示.若∠ADQ=n°,则∠BED的度数是 度(用关于n的代数式表示).
参考答案
1-5:BBCAB 6-10:DBBBB 11-12:DC
13、1
14、12x2-10x+2y
15、42
16、42
17、1或者6
(1)图略
由题可得,△ABC先向下平移2个单位,再向左平移5个单位得到△A′B′C′.或△ABC先向左平移5个单位,再向下平移2个单位得到△A′B′C′
19、
20、:(1)5.
(2)-3.
(3)点P表示的数为或-3
21、:(1)(8-2)×(8-1)=6×7=42
(2)4620÷42=110(元),
(a-2b)×(a-b)
22、:(1)作EH∥PQ.
∵EH∥PQ,PQ∥MN,
∴EH∥MN,
∴∠PDE=∠DEH,∠MBE=∠BEH,
∴∠DEB=∠DEH+∠BEH=∠PDE+∠MBE.
(2)①∵∠CBN=100°,
∴∠MBC=80°,
∵BE平分∠MBC,
∴∠MBE=40°,
∵∠ADQ=130°,
∴∠PDA=50°,
∵ED平分∠PDA,
∴∠PDE=25°,
∴∠BED=∠PDE+∠MBE=25°+40°=65°.
一.选择题(共12小题)
1.下列现象中是平移的是( )
A.将一张纸沿它的中线折叠 B.电梯的上下移动
C.飞碟的快速转动 D.翻开书中的每一页纸张
2.如图,直线L1是由直线L2平移得到的,若∠1=56°,则∠2的度数为( )
A.∠2=56°
B.∠2=124°
C.∠2=134°
D.∠2=114°
3.第七届世界军人运动会(7thCISMMilitaryWorldGames),于2019年10月18日至27日在中国武汉举行,图中是吉祥物“兵兵”,将图中的“兵兵”通过平移可得到图为( )
4.如图是6级台阶侧面示意图,如果要在台阶上铺红地毯,那么地毯长度至少需要( )
A.8米
B.5米
C.4米
D.3米
5.为构建和谐校园,营造良好的教育范围,某学校服在如图所示的长方形草坪上修建甬道,道路的宽忽略不计,若草坪周长为320m,则道路的总长为( )
A.120m
B.160m
C.240m
D.320m
6.如图,在△ABC中,AB=5,AC=3,BC=7,AI平分∠BAC,CI平分∠ACB,将∠BAC平移,使其顶点与点I重合,则图中阴影部分的周长为( )
A.5
B.8
C.10
D.7
7.如图,将周长为12cm的△ABC沿边BC向右平移3cm得到△A′B′C′,则四边形ABC′A′的周长为( )
A.17cm
B.18cm
C.19cm
D.20cm
8.如图,两个形状、大小完全相同的三角形ABC和三角形DEF重叠在一起,固定三角形ABC不动,将三角形DEF向右平移,当点E和点C重合时,停止移动,设DE交AC于G.给出下列结论:
①四边形ABEG的面积与CGDF的面积相等;
②AD∥EC,且AD=EC,
则( )
A.①,②都正确
B.①正确,②错误
C.①,②都错误
D.①错误,②正确
9.如图,表示直线a平移得到直线b的两种画法,下列关于三角板平移的方向和移动的距离说法正确的是( )
A.方向相同,距离相同
B.方向不同,距离不同
C.方向相同,距离不同
D.方向不同,距离相同
10.如图,将△ABC沿着某一方向平移一定的距离得到△DEF,则下列结论:
①AD=CF;②AC∥DF;③∠ABC=∠DFE;④∠DAE=∠AEB.
正确的个数为( )
A.4个
B.3个
C.2个
D.1个
11.如图,两个直角三角形重叠在一起,将其中一个沿点B到点C的方向平移到△DEF的位置,AB=10,DH=4,BC=15,平移距离为6,则阴影部分的面积( )
A.40
B.42
C.45
D.48
12.如图,有两条长分别为a、b的铁丝,其中长为a的铁丝恰好围成一个大正方形;AB是大正方形的对角线,把AB分成n条相等的线段,再以每条线段作为小正方形的对角线,长为b的铁丝恰好能围成n个这样的小正方形;若均不考虑接口情况,则a、b的大小关系是( )
A.a>b
B.a<b
C.a=b
D.a≥b
二.填空题(共5小题)
13.如图,将周长为18cm的△ABC沿BC平移1cm得到△DEF.则AD= cm.
14.如图,某小区规划在长,宽分别为4x,3x的长方形场地上,修建三条互相垂直且宽均为y米的甬道(单位:m),其余阴影部分种草,则阴影部分的面积为 (用含x、y的式子表示,并计算出最终结果.)
15.如图,多边形的相邻两边均互相垂直,则这个多边形的周长为 .
16.如图,长8米宽6米的草坪上有一条弯折的小路(小路进出口的宽度相等,且每段小路均为平行四边形),小路进出口的宽度均为1米,则绿地的面积为 平方米.
17.已知,大正方形的边长为5厘米,小正方形的边长为2厘米,起始状态如图所示.大正方形固定不动,把小正方形以1厘米/秒的速度向右沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S平方厘米.当S=2时,小正方形平移的时间为 秒.
三.解答题(共5小题)
18.在如图网格坐标系中,△ABC的各顶点均位于格点处,其中网格小正方形的边长为1个单位.
(1)平移△ABC,使得点A平移到点A′处,作出平移后的△A′B′C′;
(2)请说出△ABC是通过怎样的平移得到△A′B′C′.
19.如图,已知△ABC在平面直角坐标系中的位置如图所示,
(1)写出△ABC三个顶点的坐标;
(2)求出△ABC的面积;
(3)在图中画出把△ABC先向左平移5个单位,再向上平移2个单位后所得的△A′B′C′,并写出各顶点坐标.
20.操作与探究:对数轴上的任意一点P.
①作出点N使得N和P表示的数互为相反数,再把N对应的点向右平移1个单位,得到点P的对应点P′.我们称P′是P的N变换点;
②把P点向右平移1个单位,得到点M,作出点P′′使得P′′和M表示的数互为相反数,我们称P′′是P的M变换点.
(1)如图,若点P表示的数是-4,则P的N变换点P′表示的数是 ;
(2)若P的M变换点P′′表示的数是2,则点P表示的数是 ;
(3)若P′,P′′分别为P的N变换点和M变换点,且OP′=2OP′′,求点P表示的数.
21.如图,一块边长为8米的正方形土地,在上面修了三条道路,宽都是1米,空白的部分种上各种花草.
(1)请利用平移的知识求出种花草的面积.
(2)若空白的部分种植花草共花费了4620元,则每平方米种植花草的费用是多少元?
(3)如图,一块边长为a米的正方形土地,在上面修了3条道路,宽都是b米,空白的部分种上各种花草,则求出种花草的面积.
22.(1)如图1,已知MN∥PQ,B在MN上,D在PQ上,点E在两平行线之间,求证:∠BED=∠PDE+∠MBE;
(2)如图2,已知MN∥PQ,B在MN上,C在PQ上,A在B的左侧,D在C的右侧,DE平分∠ADC,BE平分∠ABC,直线DE、BE交于点E,∠CBN=100°.
①若∠ADQ=130°,求∠BED的度数;
②将线段AD沿DC方向平移,使得点D在点C的左侧,其他条件不变,如图3所示.若∠ADQ=n°,则∠BED的度数是 度(用关于n的代数式表示).
参考答案
1-5:BBCAB 6-10:DBBBB 11-12:DC
13、1
14、12x2-10x+2y
15、42
16、42
17、1或者6
(1)图略
由题可得,△ABC先向下平移2个单位,再向左平移5个单位得到△A′B′C′.或△ABC先向左平移5个单位,再向下平移2个单位得到△A′B′C′
19、
20、:(1)5.
(2)-3.
(3)点P表示的数为或-3
21、:(1)(8-2)×(8-1)=6×7=42
(2)4620÷42=110(元),
(a-2b)×(a-b)
22、:(1)作EH∥PQ.
∵EH∥PQ,PQ∥MN,
∴EH∥MN,
∴∠PDE=∠DEH,∠MBE=∠BEH,
∴∠DEB=∠DEH+∠BEH=∠PDE+∠MBE.
(2)①∵∠CBN=100°,
∴∠MBC=80°,
∵BE平分∠MBC,
∴∠MBE=40°,
∵∠ADQ=130°,
∴∠PDA=50°,
∵ED平分∠PDA,
∴∠PDE=25°,
∴∠BED=∠PDE+∠MBE=25°+40°=65°.
