北师大版数学七年级下册4.1认识三角形(第2课时 三角形的三边关系)教案
文档属性
| 名称 | 北师大版数学七年级下册4.1认识三角形(第2课时 三角形的三边关系)教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-03 10:03:48 | ||
图片预览



文档简介
4.1 认识三角形(第2课时 三角形的三边关系)
教学目标
1.结合具体实例,认识等腰三角形和等边三角形的概念及基本要素.
2.在度量三角形边长的实践活动中理解三角形三边的关系.
3.掌握三角形三边的关系,并能解决相关问题.
教学重点难点
重点:三角形的三边关系.
难点:探究三角形的三边关系及灵活应用三边关系解决生活中的实际问题.
课时安排
1课时
教学过程
导入新课
我们已经学习了按角对三角形进行分类,大家还记得吗?
三角形
能否按照边对三角形进行分类呢?
探究新知
一、三角形按边分类
问题1:你能找出下列三角形各自的特点吗?
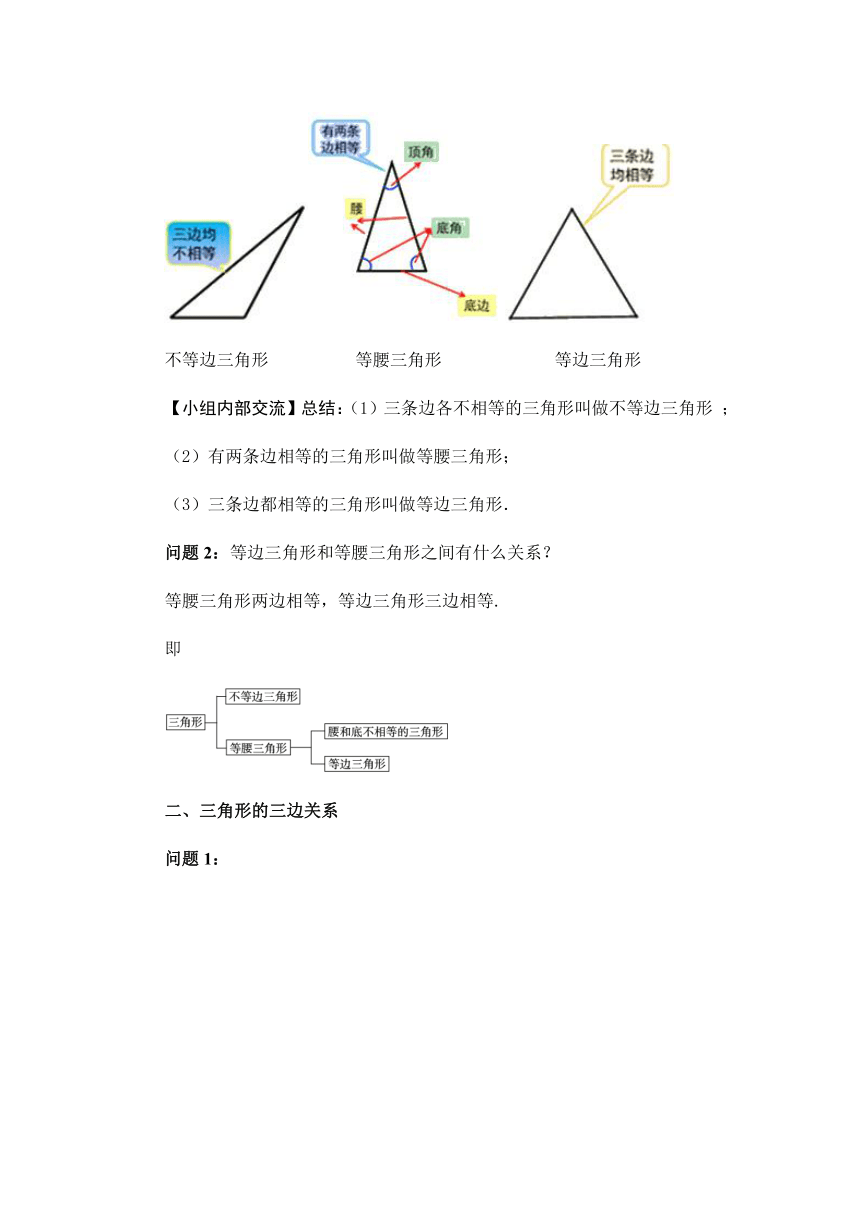
不等边三角形 等腰三角形 等边三角形
【小组内部交流】总结:(1)三条边各不相等的三角形叫做不等边三角形 ;
(2)有两条边相等的三角形叫做等腰三角形;
(3)三条边都相等的三角形叫做等边三角形.
问题2:等边三角形和等腰三角形之间有什么关系?
等腰三角形两边相等,等边三角形三边相等.
即
二、三角形的三边关系
问题1:
路线1:沿从B到C再到A的路线走;
路线2:沿线段BA走.
请问:路线1、路线2哪条路程较短,你能说出根据吗?
解:路线2较短;两点之间线段最短.
由此可以得到:
AC+BC>AB
AB+BC>AC
AC+AB>BC
【小组内部交流】老师引导得出结论
探究:元宵节的晚上,房梁上亮起了彩灯,装有黄色彩灯的电线与装有红色彩灯的电线哪根长呢?说明你的理由.
方法1:测量可以得出.
方法2:根据“两点之间的所有连线中,线段最短”的结论,可以得出.
【小组内部讨论】学生找出多种方法,老师点评.
问题2:若改变各边的颜色呢?你可以得到什么结论?说明你的理由.利用你发现的规律填空:
> .
> .
讨论:1.在同一个三角形中,任意两边之和与第三边有什么大小关系?
2.在同一个三角形中,任意两边之差与第三边有什么大小关系?
3.三角形三边有怎样的关系?
通过动手实验,同学们可以得到哪些结论?
【小组内部讨论】(老师引导学生总结)三角形两边的和大于第三边.三角形两边的差小于第三边.
例1 有两根长度分别为5cm和8cm的木棒,用长度为2cm的木棒与它们能摆成三角形吗?为什么?长度为13cm的木棒呢?
解:取长度为2cm的木棒时,
由于2+5=7<8,出现了两边之和小于第三边的情况,
所以它们不能摆成三角形.
取长度为13cm的木棒时,
由于5+8=13,出现了两边之和等于第三边的情况,
所以它们也不能摆成三角形.
例2 判断下列长度的三条线段能否拼成三角形?为什么?
(1)3cm、8cm、4cm; (2)5cm、6cm、11cm;
(3)5cm、6cm、10cm.
解:(1)不能,因为3cm+4cm<8cm;
(2)不能,因为5cm+6cm=11cm;
(3)能,因为5cm+6cm>10cm.
【小组内部交流】(老师引导学生归纳)判断三条线段是否可以组成三角形,只需说明两条较短线段之和大于第三条线段即可.
例3 一个三角形的三边长分别为4,7,x,那么x的取值范围是( )
A.3<x<11 B.4<x<7
C.-3<x<11 D.x>3
解析:∵三角形的三边长分别为4,7,x,
∴7-4<x<7+4,即3<x<11.
答案:A
【总结】判断三角形边的取值范围要同时运用两边之和大于第三边,两边之差小于第三边.
例4 用一根长为18厘米的细铁丝围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边的长是多少?
(2)能围成有一边的长为4厘米的等腰三角形吗?
【小组内部探索】(引发学生思考)(1)理解题意,得出等腰三角形的周长是18厘米→列方程求解;
(2)等腰三角形的周长为18厘米→已知边是腰还是底边→分类讨论→得三角形另外两边长→利用三角形三边关系进行判断→得出结论.
解:(1)设底边长为x厘米,则腰长为2x厘米.
根据题意,得x+2x+2x=18,解得x=3.6.
所以三边长分别为3.6厘米、7.2厘米、7.2厘米.
(2)分情况讨论:
①当4厘米长为底边长时,设腰长为x厘米,则4+2x=18,解得x=7.
所以等腰三角形的三边长分别为7厘米、7厘米、4厘米.
②当4厘米长为腰长时,设底边长为x厘米,则4×2+x=18,解得x=10.
此时三边长分别为4厘米、4厘米、10厘米.
而4+4<10,
所以此时不能构成三角形.
故能围成底边长为4厘米,腰长为7厘米的等腰三角形.
【总结】(学生总结,老师点评)当已知等腰三角形的周长和一边长时,需要分类讨论已知的一边长是腰长还是底边长,再解决问题.
课堂练习
1.判断:
(1)一个钝角三角形一定不是等腰三角形.( )
(2)等边三角形是特殊的等腰三角形.( )
(3)等腰三角形的腰和底一定不相等.( )
(4)等边三角形是锐角三角形.( )
(5)直角三角形一定不是等腰三角形.( )
2.用木棒钉成一个三角架,两根小棒分别是7cm,10cm,第三根小棒可取( )
A.20cm B.3cm C.11cm D.2cm
3.如果等腰三角形的一边长是5cm,另一边长是8cm,则这个等腰三角形的周长为______________.
4.已知等腰三角形的周长为18cm,如果一边长等于4cm,求另两边的长.
5.若a,b,c是△ABC的三边长,化简|a-b-c|+|b-c-a|+|c+a-b|.
参考答案
1.(1)×(2)√(3)×(4)√(5)×
2.C
3.18cm或21cm
4.解:若底边长为4cm,设腰长为x cm,则2x+4=18,解得x=7.
若一条腰长为4cm,设底边长为x cm,则2×4+x=18,解得x=10.
因为4+4<10,所以4cm为腰不能构成三角形.
所以三角形另外两个边长都是7cm.
5.解:根据三角形的三边关系,得a-b-c<0,b-c-a<0,c+a-b>0.
∴|a-b-c|+|b-c-a|+|c+a-b|
=b+c-a+c+a-b+c+a-b
=3c+a-b.
课堂小结
布置作业
习题4.2
板书设计
三角形的三边关系
1.等腰三角形:有两边相等的三角形.
2.等边三角形:三边都相等的三角形.
3.三角形的三边关系:三角形任意两边之和大于第三边,任意两边之差小于第三边.
C
B
A
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
