北师大版数学九年级上册1.1.1 菱形及其性质 课件(25张ppt)
文档属性
| 名称 | 北师大版数学九年级上册1.1.1 菱形及其性质 课件(25张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-03 10:32:59 | ||
图片预览






文档简介
课件25张PPT。1.1 菱形的性质与判定第1课时 菱形及其性质北师大版数学九年级上册1课堂讲解2课时流程逐点
导讲练课堂小结作业提升菱形的定义
菱形边的性质
菱形对角线的性质 下面几幅图片中都含有一些平行四边形.观察这些平行四边形,你能发现它们有什么样的共同特征?
1知识点菱形的定义菱形的定义:有一组邻边相等的平行四边形叫做菱形.
要点精析:
(1)菱形必须满足两个条件:一是平行四边形;二是一组
邻边相等.二者必须同时具备,缺一不可.
(2)菱形的定义既是菱形的基本性质,也是菱形的基本判
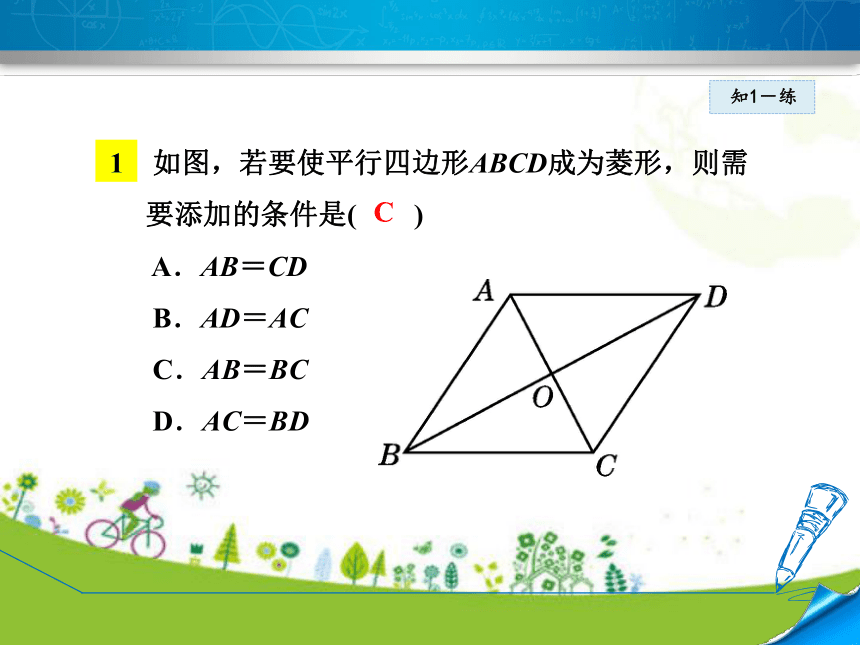
定方法.知1-讲如图,若要使平行四边形ABCD成为菱形,则需
要添加的条件是( )
A.AB=CD
B.AD=AC
C.AB=BC
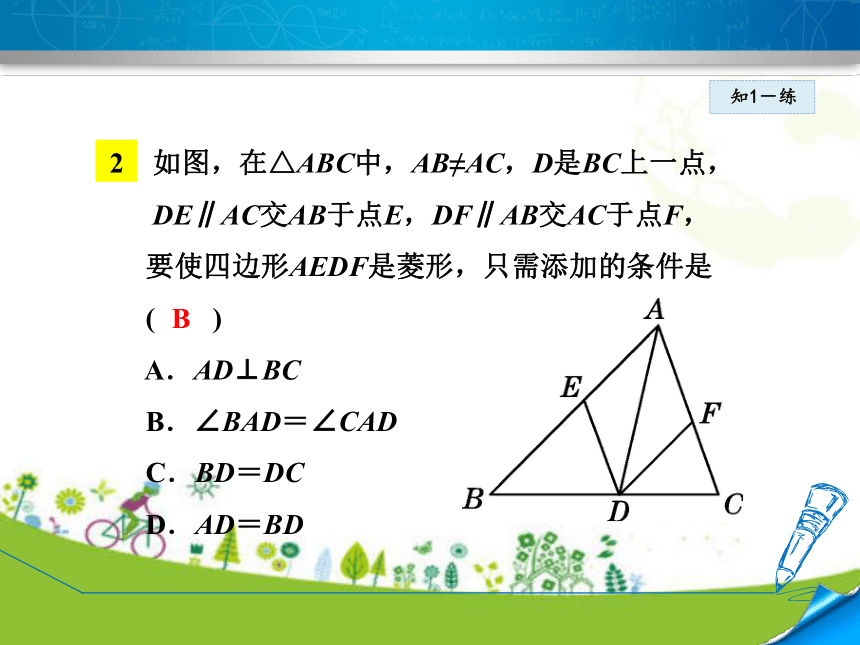
D.AC=BD知1-练 C如图,在△ABC中,AB≠AC,D是BC上一点,
DE∥AC交AB于点E,DF∥AB交AC于点F,
要使四边形AEDF是菱形,只需添加的条件是
( )
A.AD⊥BC
B.∠BAD=∠CAD
C.BD=DC
D.AD=BD知1-练 B2知识点菱形边的性质知2-导 菱形具有平行四边形的所有性质.此外,菱形
还具有哪些特殊性质呢? 根据菱形的轴对称性,你
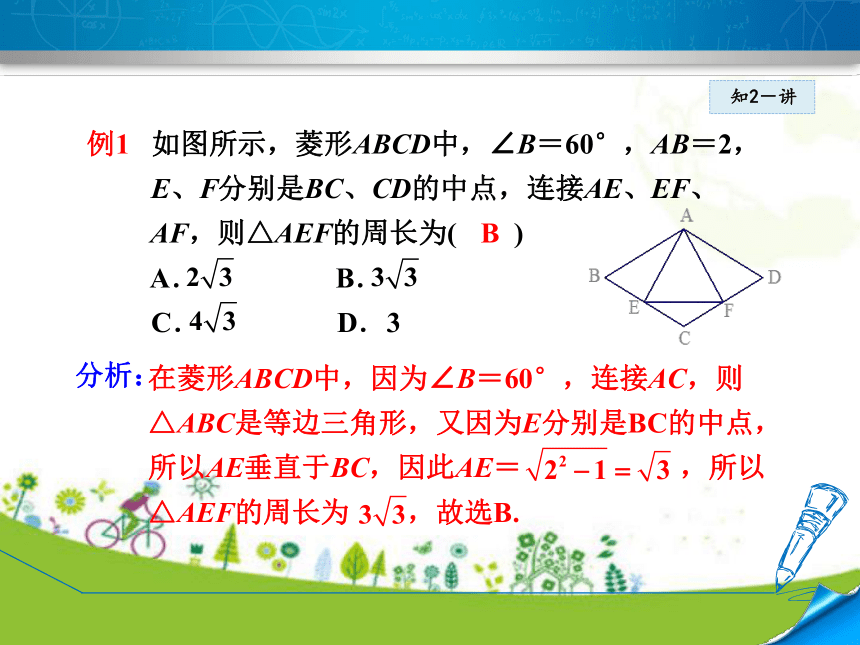
发现菱形的四条边具有什么大小关系?问 题菱形的四条边都相等.知2-讲例1 如图所示,菱形ABCD中,∠B=60°,AB=2,
E、F分别是BC、CD的中点,连接AE、EF、
AF,则△AEF的周长为( )
A. B.
C. D.3 在菱形ABCD中,因为∠B=60°,连接AC,则
△ABC是等边三角形,又因为E分别是BC的中点,
所以AE垂直于BC,因此AE= ,所以
△AEF的周长为 ,故选B.B分析:知2-讲 在菱形中作辅助线经常连接对角线,构造
三角形来做题,能够迎刃而解.1 边长为3 cm的菱形的周长是( )
A.6 cm B.9 cm
C.12 cm D.15 cm知2-练 C知2-练如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=3,那么菱形ABCD的周长为( )
A.24 B.18 C.12 D. 9 A3知识点菱形对角线的性质知3-导 因为菱形是平行四边形,所以它具有平行四边形的
所有性质.由于它的一组邻边相等,它是否具有一般平行
四边形不具有的一些特殊性质呢?思考菱形的两条对角线AC与BD之间具有什么位置关系?知3-导已知:如图,在菱形ABCD中,AB=AD,对角线AC与BD相交于点O.求证(1)AB=BC=CD=AD,(2)AC⊥BD.
证明:
(1)∵四边形ABCD是菱形,
∴AB=CD,AD=BC(菱形的对边相等).
又∵AB=AD,∴AB=BC=CD=AD.
(2)∵AB=AD,∴△ABD是等腰三角形.
又∵四边形ABCD是菱形,∴OB=OD(菱形的对角线互相平分).
在等腰三角形ABD中,∵OB=OD,∴AO⊥BD,
即 AC⊥BD.知3-导定理 菱形的对角线互相垂直.知3-导问 题菱形的面积如何计算呢?菱形的面积有两种计算方法:
一种是底乘以高的积;
另一种是对角线乘积的一半.所以在求菱形的面积
时,要灵活运用使计算简单.由于菱形的四条边都相等,
所以要求其周长就要先求
出其边长.由菱形的性质
可知,其对角线互相垂直平分,因此可以在直角
三角形中利用勾股定理来进行计算.知3-讲例2 如图,在菱形ABCD中,对角线AC与BD相交于
点O,BD=12 cm,AC=6 cm.求菱形的周长.导引:∵四边形ABCD是菱形,
∴AC⊥BD,AO= AC,BO= BD.
∵AC=6 cm,BD=12 cm,
∴AO=3 cm,BO=6 cm.
在Rt△ABO中,由勾股定理,
得AB=
∴菱形的周长=4AB知3-讲解:知3-讲 菱形的对角线将菱形分成四个全等的直角三角
形,我们通常将菱形问题中求相关线段的长转化为
求直角三角形中相关线段的长,再利用勾股定理来
计算.1 如图,四边形ABCD是菱形,BE⊥AD,BF⊥CD,
垂足分别为E,F.
(1)求证:BE=BF;
(2)当菱形ABCD的对角线AC=8,BD=6时,
求BE的长.知3-练知3-练知3-练如图,菱形ABCD的对角线AC,BD的长分别为6和8则这个菱形的周长是( )
A. 20 B. 24 C. 40 D. 48知3-练A1.必做: 完成教材P4——P5,T1-T4
2.补充: 请完成《点拨训练》P2—P3对应习题!谢谢!
导讲练课堂小结作业提升菱形的定义
菱形边的性质
菱形对角线的性质 下面几幅图片中都含有一些平行四边形.观察这些平行四边形,你能发现它们有什么样的共同特征?
1知识点菱形的定义菱形的定义:有一组邻边相等的平行四边形叫做菱形.
要点精析:
(1)菱形必须满足两个条件:一是平行四边形;二是一组
邻边相等.二者必须同时具备,缺一不可.
(2)菱形的定义既是菱形的基本性质,也是菱形的基本判
定方法.知1-讲如图,若要使平行四边形ABCD成为菱形,则需
要添加的条件是( )
A.AB=CD
B.AD=AC
C.AB=BC
D.AC=BD知1-练 C如图,在△ABC中,AB≠AC,D是BC上一点,
DE∥AC交AB于点E,DF∥AB交AC于点F,
要使四边形AEDF是菱形,只需添加的条件是
( )
A.AD⊥BC
B.∠BAD=∠CAD
C.BD=DC
D.AD=BD知1-练 B2知识点菱形边的性质知2-导 菱形具有平行四边形的所有性质.此外,菱形
还具有哪些特殊性质呢? 根据菱形的轴对称性,你
发现菱形的四条边具有什么大小关系?问 题菱形的四条边都相等.知2-讲例1 如图所示,菱形ABCD中,∠B=60°,AB=2,
E、F分别是BC、CD的中点,连接AE、EF、
AF,则△AEF的周长为( )
A. B.
C. D.3 在菱形ABCD中,因为∠B=60°,连接AC,则
△ABC是等边三角形,又因为E分别是BC的中点,
所以AE垂直于BC,因此AE= ,所以
△AEF的周长为 ,故选B.B分析:知2-讲 在菱形中作辅助线经常连接对角线,构造
三角形来做题,能够迎刃而解.1 边长为3 cm的菱形的周长是( )
A.6 cm B.9 cm
C.12 cm D.15 cm知2-练 C知2-练如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=3,那么菱形ABCD的周长为( )
A.24 B.18 C.12 D. 9 A3知识点菱形对角线的性质知3-导 因为菱形是平行四边形,所以它具有平行四边形的
所有性质.由于它的一组邻边相等,它是否具有一般平行
四边形不具有的一些特殊性质呢?思考菱形的两条对角线AC与BD之间具有什么位置关系?知3-导已知:如图,在菱形ABCD中,AB=AD,对角线AC与BD相交于点O.求证(1)AB=BC=CD=AD,(2)AC⊥BD.
证明:
(1)∵四边形ABCD是菱形,
∴AB=CD,AD=BC(菱形的对边相等).
又∵AB=AD,∴AB=BC=CD=AD.
(2)∵AB=AD,∴△ABD是等腰三角形.
又∵四边形ABCD是菱形,∴OB=OD(菱形的对角线互相平分).
在等腰三角形ABD中,∵OB=OD,∴AO⊥BD,
即 AC⊥BD.知3-导定理 菱形的对角线互相垂直.知3-导问 题菱形的面积如何计算呢?菱形的面积有两种计算方法:
一种是底乘以高的积;
另一种是对角线乘积的一半.所以在求菱形的面积
时,要灵活运用使计算简单.由于菱形的四条边都相等,
所以要求其周长就要先求
出其边长.由菱形的性质
可知,其对角线互相垂直平分,因此可以在直角
三角形中利用勾股定理来进行计算.知3-讲例2 如图,在菱形ABCD中,对角线AC与BD相交于
点O,BD=12 cm,AC=6 cm.求菱形的周长.导引:∵四边形ABCD是菱形,
∴AC⊥BD,AO= AC,BO= BD.
∵AC=6 cm,BD=12 cm,
∴AO=3 cm,BO=6 cm.
在Rt△ABO中,由勾股定理,
得AB=
∴菱形的周长=4AB知3-讲解:知3-讲 菱形的对角线将菱形分成四个全等的直角三角
形,我们通常将菱形问题中求相关线段的长转化为
求直角三角形中相关线段的长,再利用勾股定理来
计算.1 如图,四边形ABCD是菱形,BE⊥AD,BF⊥CD,
垂足分别为E,F.
(1)求证:BE=BF;
(2)当菱形ABCD的对角线AC=8,BD=6时,
求BE的长.知3-练知3-练知3-练如图,菱形ABCD的对角线AC,BD的长分别为6和8则这个菱形的周长是( )
A. 20 B. 24 C. 40 D. 48知3-练A1.必做: 完成教材P4——P5,T1-T4
2.补充: 请完成《点拨训练》P2—P3对应习题!谢谢!
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
