华东师大版七年级数学下册 9.1.2三角形的内角和与外角和 一课一练(含答案)
文档属性
| 名称 | 华东师大版七年级数学下册 9.1.2三角形的内角和与外角和 一课一练(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 131.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-03 15:11:37 | ||
图片预览


文档简介
9.1.2三角形的内角和与外角和
A组
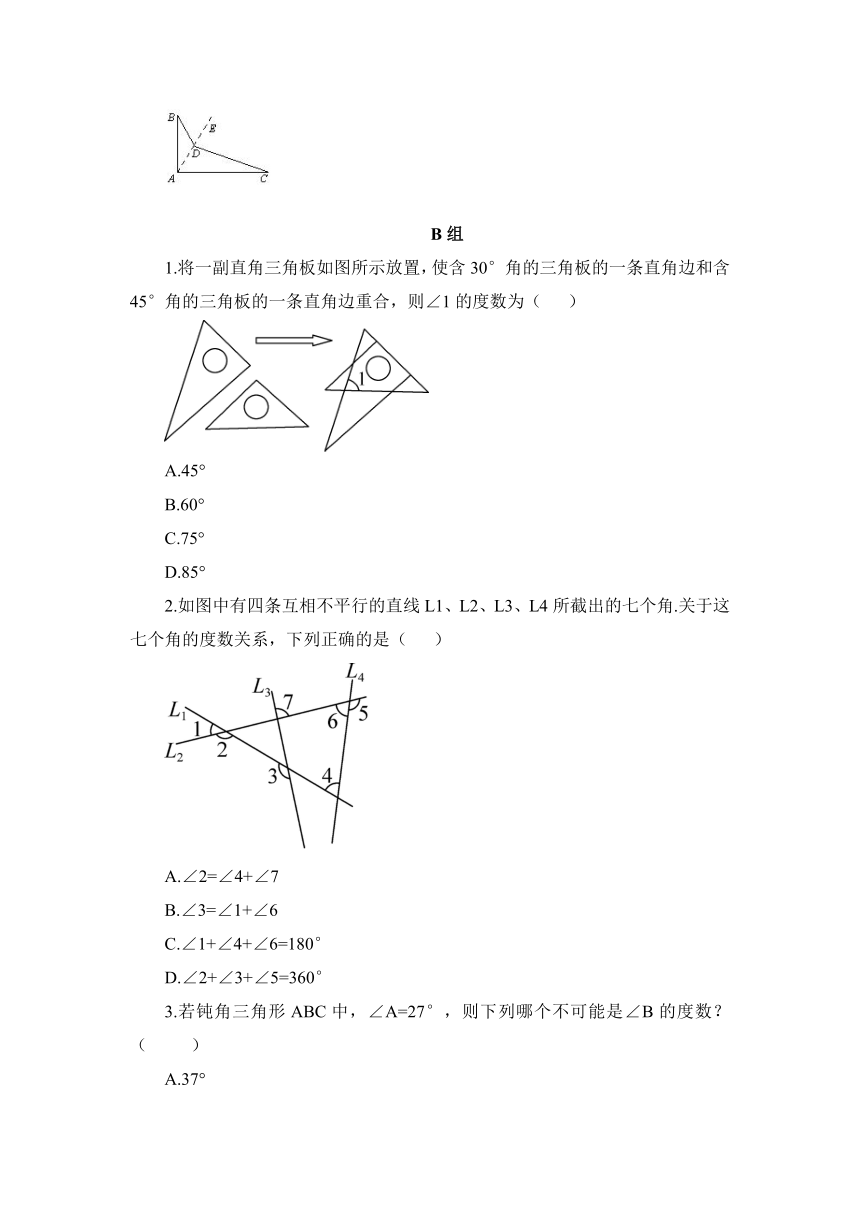
1.如图,下列关于外角的说法是否正确:
(1)∠1是△ABC的外角( )
(2)∠2是△ABC的外角( )
(3)∠3是△ABC的外角( )
(4)∠4是△ABC的外角( )
2.判断:
(1)一个三角形至少有两个外角是钝角。( )
(2)若一个三角形的三个外角中,有一个是锐角,则它必为锐角三角形。( )
3.如图,下列答案中错误的是:( )
A.∠3=∠ABD+∠A
B.∠1=∠3+∠PCD
C.∠1=∠ABD+∠A
D.∠1=∠A+∠ABD+∠PCD
4.如图,∠A=31°,∠B=60°,∠BFD=52°,求∠C.
5.如图,F是△ABC内部一点,求证:∠BFC=∠A+∠1+∠2
6. 一个零件的形状如图所示,按规定应等于,、应分别是和,李叔叔量得,就判定这个零件不合格,你能说出其中的道理吗?
A组
参考答案:
1.(1)错(2)错(3)错(4)对
2.(1)×(2)×
3.C
4.解:∠CEF=∠A+∠B=31°+60°=91°
∵∠C+∠CEF+∠CFE=180°
又∵∠BFD=∠CFE=52°
∴∠C+91°+52°=180°
∴∠C=37°
5.证明:连结AF并延长与BC交于D
∵∠BFD=∠1+∠BAF
∠CFD=∠2+∠CAF
又∵∠BFC=∠BFD+∠CFD
∴∠BFC=∠1+∠BAF+∠2+∠CAF
6. 四边形是凹四边形,要通过图形的构造化归为凸多边形问题.为此作射线,此时
,所以可以判定这个零件不合格.
B组
1.将一副直角三角板如图所示放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边重合,则∠1的度数为( )
A.45°
B.60°
C.75°
D.85°
2.如图中有四条互相不平行的直线L1、L2、L3、L4所截出的七个角.关于这七个角的度数关系,下列正确的是( )
A.∠2=∠4+∠7
B.∠3=∠1+∠6
C.∠1+∠4+∠6=180°
D.∠2+∠3+∠5=360°
3.若钝角三角形ABC中,∠A=27°,则下列哪个不可能是∠B的度数?( )
A.37°
B.57°
C.77°
D.97°
4.如图,l∥m,∠1=115°,∠2=95°,求∠3的度数.
第4题图 第5题图
5.如图,求∠A+∠B+∠C+∠D+∠E的度数.
6.如图,∠ABC=31°,又∠BAC的平分线AE与∠FCB的平分线CE相交于E点,求∠AEC的度数.
第6题图
7.如图,△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠DAC=30°,求∠BDC的大小.
第7题图
B组
参考答案:
1.C
2.C
3.C
4.解:∵l∥m,∠1=115°,
∴∠4=180°-∠1=180°-115°=65°,
又∠5=180°-∠2=180°-95°=85°,
∴∠3=∠4+∠5=65°+85°=150°
5.解:如图连接CE,
根据三角形的外角性质得
∠1=∠A+∠B=∠2+∠3,
在△DCE中有
∠D+∠2+∠DCB+∠3+∠AED=180°,
∴∠D+∠A+∠DCB+∠B+∠AED=180°.
6.解:设∠BAC=2x°,
则根据三角形外角的性质得:
∠BCF=(2x+31)°,
∵∠BAC的平分线与∠FCB的平分线CE相交于E点,
∴∠EAC=x°,∠ECD=(∠E+x)°,
∵∠ECF是△AEC的外角,
∠ECD=∠ECF,∴∠ECD=∠E+∠EAC,
即:∠E+(∠E+x°)=x°+31°,
解得:∠E=15.5°.
7.解:如图,延长BD交AC于E.
∵DA=DB=DC,
∴∠ABE=∠DAB=20°,∠ECD=∠DAC=30°.
又∵∠BAE=∠BAD+∠DAC=50°,∠BDC=∠DEC+∠ECD,∠DEC=∠ABE+∠BAE,
∴∠BDC=∠ABE+∠BAE+∠ECD=20°+50°+30°=100°.
