华东师大版七年级数学下册 9.1.1认识三角形(三角形的三线)教案
文档属性
| 名称 | 华东师大版七年级数学下册 9.1.1认识三角形(三角形的三线)教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 95.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-03 00:00:00 | ||
图片预览

文档简介
9.1.1认识三角形
知识技能目标
1.掌握三角形的角平分线、中线和高的概念,并会用数学式子表示;
2.掌握三角形的角平分线、中线和高的画法.
过程性目标
1.通过回忆三角形的有关概念,探索三角形的角平分线、中线和高的概念;
2.结合实践与应用,感受三角形的角平分线、中线和高的画法,体会三角形的角平分线、中线和高在三角形中的作用.
重点、难点
1.重点:三角形角平分线、中线、高的概念及其画法.
2.难点:钝角三角形高的画法.
教学过程
一、复习提问
1.什么叫角平分线?如何画一个角的平分线?
2.已知A、B分别是直线l上和直线l外一点,分别过点A、点B画直线l的垂线.
l A
·B
3.三角形按角分类可分为哪几种?
二、探索归纳
问题 已知,如图△ABC中,AD是BC边上的高,BC=3cm,AD=2cm
求:(1)△ABC的面积;
(2)若E是BC的中点,则△ABE与△ACE的面积有何关系?
三角形的面积等于底乘以高再除以2.
(板书) S△ABC=
=
=3cm2
S△ABE=,S△ACE=
因为 E是BC的中点
所以 BE=CE
故 S△ABE=S△ACE.
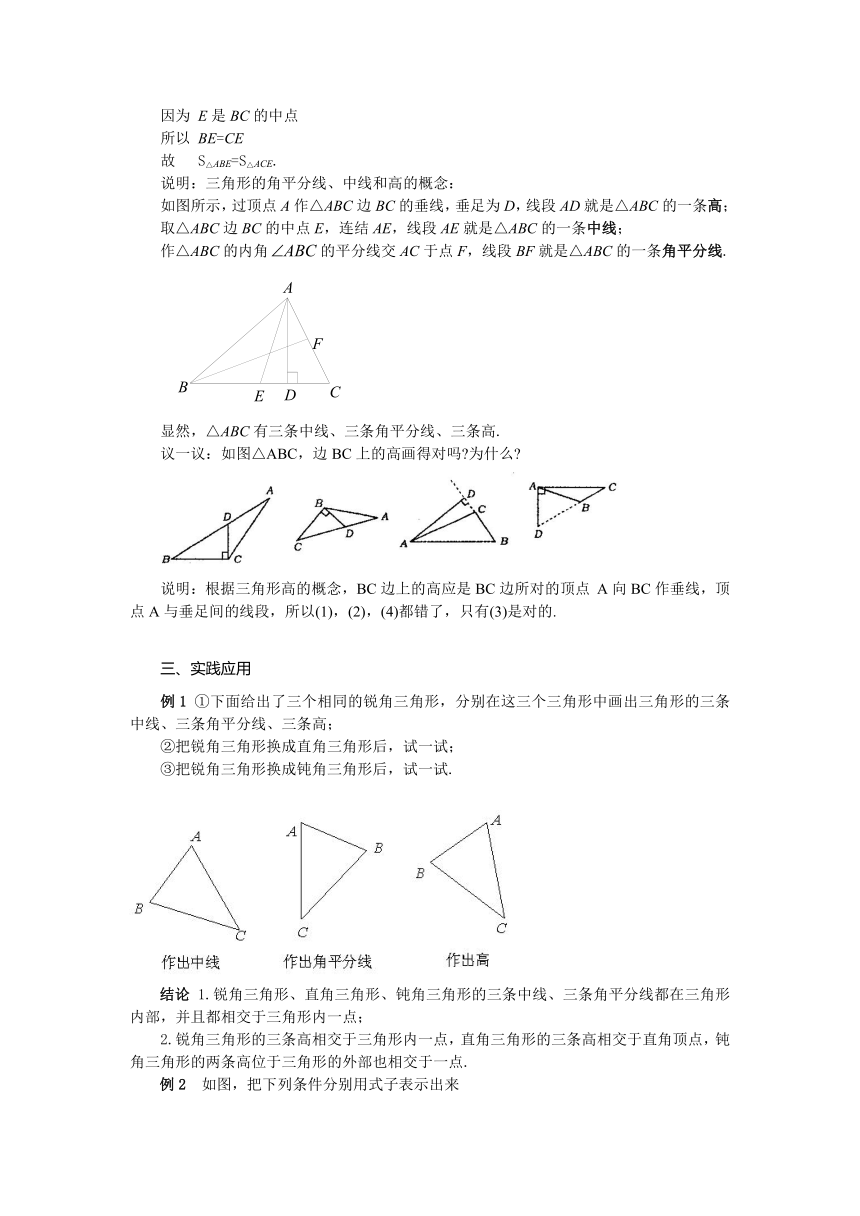
说明:三角形的角平分线、中线和高的概念:
如图所示,过顶点A作△ABC边BC的垂线,垂足为D,线段AD就是△ABC的一条高;
取△ABC边BC的中点E,连结AE,线段AE就是△ABC的一条中线;
作△ABC的内角的平分线交AC于点F,线段BF就是△ABC的一条角平分线.
显然,△ABC有三条中线、三条角平分线、三条高.
议一议:如图△ABC,边BC上的高画得对吗?为什么?
说明:根据三角形高的概念,BC边上的高应是BC边所对的顶点 A向BC作垂线,顶点A与垂足间的线段,所以(1),(2),(4)都错了,只有(3)是对的.
三、实践应用
例1 ①下面给出了三个相同的锐角三角形,分别在这三个三角形中画出三角形的三条中线、三条角平分线、三条高;
②把锐角三角形换成直角三角形后,试一试;
③把锐角三角形换成钝角三角形后,试一试.
结论 1.锐角三角形、直角三角形、钝角三角形的三条中线、三条角平分线都在三角形内部,并且都相交于三角形内一点;
2.锐角三角形的三条高相交于三角形内一点,直角三角形的三条高相交于直角顶点,钝角三角形的两条高位于三角形的外部也相交于一点.
例2 如图,把下列条件分别用式子表示出来
(1)AD是△ABC的高;
(2)BE是△ABC的角平分线;
(3)CF是△ABC的中线.
解 (1)
(2),或
(3),或
练习 (1)如图,△ABC是等腰三角形,且AB=AC,试作出BC边上的中线和高及∠A的平分线,从中你发现了什么?
(2)在一个直角三角形中,画出斜边上的中线,观察一下图形中有几个等腰三角形,再用刻度尺验证你的结论;
(3)如图,过△ABC的一个顶点A画它的角平分线AD,中线AM,高AH,写出图中相等的线段和相等的角.
四、交流反思
三角形的角平分线、中线、高的定义和画法.
五、检测反馈
1.填空
(1)如图,AD、BE、CF是△ABC的三条角平分线,则∠1=( ),∠3=( ),
∠2+∠4+∠6=( )度;
(2)如图,AD、BE、CF是△ABC的三条中线,则AB=2( ),BD=( ),若△ABC的周长为acm,则AE+CD+BF=( )cm;
2.如图,在△ABC中
(1)画出∠C的平分线CD;
(2)画出AC边上的中线BM;
(3)画出BC边上的高AH.
3.如图,已知BM是△ABC的中线,AB=5cm,BC=3cm,求△ABM与△BCM的周长的差.
六、作业
课本习题
