华东师大版七年级数学下册 9.2多边形的内角与外角和 导学案(部分有答案)
文档属性
| 名称 | 华东师大版七年级数学下册 9.2多边形的内角与外角和 导学案(部分有答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 550.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-04 00:00:00 | ||
图片预览



文档简介
9.2“多边形的内角和与外角和”导学案
编号 使用时间 小组
姓名 小组评价 教师评价
学习目标
1、了解多边形及多边形的内角、外角等概念。
2、通过不同方法探索多边形的内角和与外角和公式,并会利用它们进行有关计算。
二、自主学习
1、课前预习教材内容,勾画出重点内容,找出疑惑之处。
2、三角形的内角和等于 °,三角形的外角和等于 °。
3、一般地,由n条不在同一直线上的线段 连结组成的平面图形,记为n边形,又称多边形;如果多边形的各边都相等,各内角也都相等,则称为 多边形。
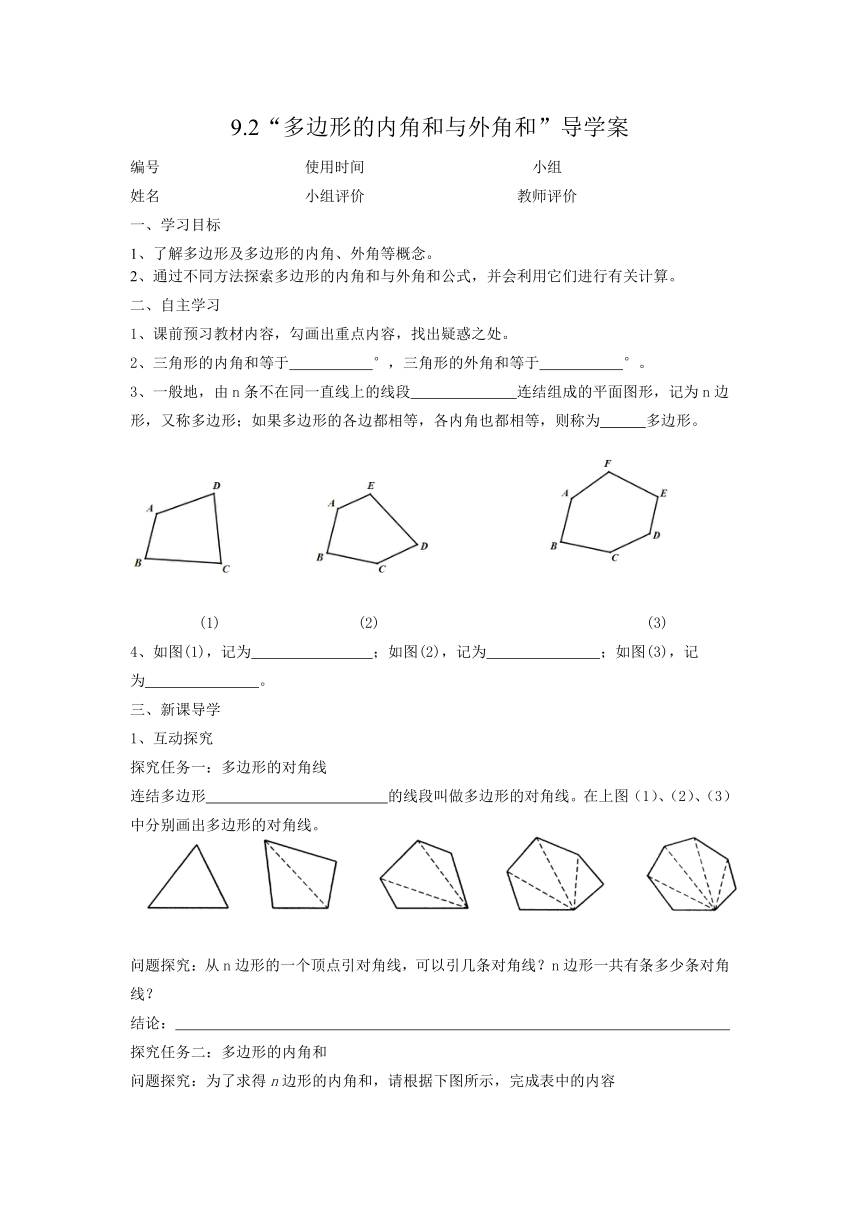
(1) (2) (3)
4、如图(1),记为 ;如图(2),记为 ;如图(3),记为 。
三、新课导学
1、互动探究
探究任务一:多边形的对角线
连结多边形 的线段叫做多边形的对角线。在上图(1)、(2)、(3)中分别画出多边形的对角线。
问题探究:从n边形的一个顶点引对角线,可以引几条对角线?n边形一共有条多少条对角线?
结论: 探究任务二:多边形的内角和
问题探究:为了求得n边形的内角和,请根据下图所示,完成表中的内容
得出结论:n边形的内角和为_________________.
探究任务三:多边形的外角和从与每个内角相邻的两个外角中分别取一个相加,得到的和称为多边形的外角和
问题探究:根据n边形的每一个内角与它的相邻的外角都互为补角,可以求得n边形的外角和.为了求得n边形的外角和,请将数据填入表
任意多边形的外角和都为________.
2、探究升华
例1.一个多边形的内角和等于2340°,求它的边数。
变式:一个正多边形的一个内角为150°,你知道它是几边形?
小结: 知道一个多边形的内角和,根据n边形的内角和=(n-2)·180°可以求边数n。
例2、一个正多边形的一个内角比相邻外角大36°,求这个正多边形的边数。
四、当堂检测
1、十边形的内角和是________,外角和是_________;如果十边形的各个内角都相等,那么它的一个内角是 。
2、如果一个正多边形的每个外角是24°,那么这个多边形是( )边形。
A、14 B、15 C、25 D、35
3、(n+1)边形的内角和比n边形的内角和大( )
A、180° B、360° C、180n D、360n
4、四边形ABCD中,∠C和∠A互为补角,且∠A∶∠B∶∠D=6∶4∶5,求∠C的度数。
已知一个多边形共有9条对角线,求这个多边形的内角和的度数。
课后小测试
1.如果一个多边形的内角和是它的外角和的3倍,那么这个多边形是( )
A.九边形
B.八边形
C.七边形
D.六边形
2.若n边形的内角和与外角和的比为7∶2,则n为( )
A.6
B.7
C.8
D.9
3.如果一个正多边形的一个内角和它相邻外角的比是2∶1,那么这个多边形是( )
A.正六边形
B.正八边形
C.正十边形
D.正十二边形
4.四边形的内角和为 度,四个内角中最多可有 个锐角.
5.若四边形的四个内角之比为1∶3∶5∶6,则这个四边形各内角顺次
是 度.
6.多边形的每一个内角都相等,它的一个外角等于正十边形的一个内角的
.求这个多边形的边数.
7.(1)一个多边形的内角和等于2340°,求它的边数;
(2)一个正多边形的一个内角为150°,你知道它是几边形吗?
8.一个正多边形的一个内角比相邻外角大36°,求这个正多边形的边数.
9.(1)四边形有几条对角线?
(2)五边形有几条对角线?六边形呢?n边形呢?
10.已知多边形的内角和等于1440°,求(1)这个多边形的边数,(2)过一个顶点有几条对角线,(3)总对角线条数.
参考答案:
1.B
2.D
3.A
4.360, 3
5.24,72,120,144
6. 6
7.解:(1)设边数为n,则有
(n-2)·180°=2340°
n-2=13, n=15;
(2)设这个多边形为n边形,则有(n-2)·180°=150°n
n=12
这个多边形是十二边形.
8.分析:正多边形的各个内角都相等,那么各个外角也都相等,而多边形的外角和是360°.
解:设一个外角为x°,则内角为(x+36)°
因为多边形的内角与相邻的外角互补;
所以 x°+x°+36°=180°
解得 x°=72°
360°÷72°=5
答:这个多边形是五边形.
9.解:(1)四边形有两条对角线.
(2)如图2,以A为顶点的对角线有两条AC、AD同样以B为端点的对角线也有2条,以C为端点也有2条,但AC与CA是同一条线段,以D为端点的两条DA、DB与AD、BD分别表示同一条线段,所以只有5条,以此类推六边形有9条对角线,从以上分析可知从n边形的一个顶点引对角线,可以引(n-3)条,那么n个顶点就有n(n-3)条,但其中每一条都重复计算一次,所以n边形一共有条对角线.
10.解:(1)(n-2)·180°=1440°
n=10
(2)n-3=10-3=7
答:这个多边形是十边形,过一个顶点的对角线有7条,共有35条对角线.
编号 使用时间 小组
姓名 小组评价 教师评价
学习目标
1、了解多边形及多边形的内角、外角等概念。
2、通过不同方法探索多边形的内角和与外角和公式,并会利用它们进行有关计算。
二、自主学习
1、课前预习教材内容,勾画出重点内容,找出疑惑之处。
2、三角形的内角和等于 °,三角形的外角和等于 °。
3、一般地,由n条不在同一直线上的线段 连结组成的平面图形,记为n边形,又称多边形;如果多边形的各边都相等,各内角也都相等,则称为 多边形。
(1) (2) (3)
4、如图(1),记为 ;如图(2),记为 ;如图(3),记为 。
三、新课导学
1、互动探究
探究任务一:多边形的对角线
连结多边形 的线段叫做多边形的对角线。在上图(1)、(2)、(3)中分别画出多边形的对角线。
问题探究:从n边形的一个顶点引对角线,可以引几条对角线?n边形一共有条多少条对角线?
结论: 探究任务二:多边形的内角和
问题探究:为了求得n边形的内角和,请根据下图所示,完成表中的内容
得出结论:n边形的内角和为_________________.
探究任务三:多边形的外角和从与每个内角相邻的两个外角中分别取一个相加,得到的和称为多边形的外角和
问题探究:根据n边形的每一个内角与它的相邻的外角都互为补角,可以求得n边形的外角和.为了求得n边形的外角和,请将数据填入表
任意多边形的外角和都为________.
2、探究升华
例1.一个多边形的内角和等于2340°,求它的边数。
变式:一个正多边形的一个内角为150°,你知道它是几边形?
小结: 知道一个多边形的内角和,根据n边形的内角和=(n-2)·180°可以求边数n。
例2、一个正多边形的一个内角比相邻外角大36°,求这个正多边形的边数。
四、当堂检测
1、十边形的内角和是________,外角和是_________;如果十边形的各个内角都相等,那么它的一个内角是 。
2、如果一个正多边形的每个外角是24°,那么这个多边形是( )边形。
A、14 B、15 C、25 D、35
3、(n+1)边形的内角和比n边形的内角和大( )
A、180° B、360° C、180n D、360n
4、四边形ABCD中,∠C和∠A互为补角,且∠A∶∠B∶∠D=6∶4∶5,求∠C的度数。
已知一个多边形共有9条对角线,求这个多边形的内角和的度数。
课后小测试
1.如果一个多边形的内角和是它的外角和的3倍,那么这个多边形是( )
A.九边形
B.八边形
C.七边形
D.六边形
2.若n边形的内角和与外角和的比为7∶2,则n为( )
A.6
B.7
C.8
D.9
3.如果一个正多边形的一个内角和它相邻外角的比是2∶1,那么这个多边形是( )
A.正六边形
B.正八边形
C.正十边形
D.正十二边形
4.四边形的内角和为 度,四个内角中最多可有 个锐角.
5.若四边形的四个内角之比为1∶3∶5∶6,则这个四边形各内角顺次
是 度.
6.多边形的每一个内角都相等,它的一个外角等于正十边形的一个内角的
.求这个多边形的边数.
7.(1)一个多边形的内角和等于2340°,求它的边数;
(2)一个正多边形的一个内角为150°,你知道它是几边形吗?
8.一个正多边形的一个内角比相邻外角大36°,求这个正多边形的边数.
9.(1)四边形有几条对角线?
(2)五边形有几条对角线?六边形呢?n边形呢?
10.已知多边形的内角和等于1440°,求(1)这个多边形的边数,(2)过一个顶点有几条对角线,(3)总对角线条数.
参考答案:
1.B
2.D
3.A
4.360, 3
5.24,72,120,144
6. 6
7.解:(1)设边数为n,则有
(n-2)·180°=2340°
n-2=13, n=15;
(2)设这个多边形为n边形,则有(n-2)·180°=150°n
n=12
这个多边形是十二边形.
8.分析:正多边形的各个内角都相等,那么各个外角也都相等,而多边形的外角和是360°.
解:设一个外角为x°,则内角为(x+36)°
因为多边形的内角与相邻的外角互补;
所以 x°+x°+36°=180°
解得 x°=72°
360°÷72°=5
答:这个多边形是五边形.
9.解:(1)四边形有两条对角线.
(2)如图2,以A为顶点的对角线有两条AC、AD同样以B为端点的对角线也有2条,以C为端点也有2条,但AC与CA是同一条线段,以D为端点的两条DA、DB与AD、BD分别表示同一条线段,所以只有5条,以此类推六边形有9条对角线,从以上分析可知从n边形的一个顶点引对角线,可以引(n-3)条,那么n个顶点就有n(n-3)条,但其中每一条都重复计算一次,所以n边形一共有条对角线.
10.解:(1)(n-2)·180°=1440°
n=10
(2)n-3=10-3=7
答:这个多边形是十边形,过一个顶点的对角线有7条,共有35条对角线.
