冀教版数学九年级上册24.2.5 因式分解法 课件(26张ppt)
文档属性
| 名称 | 冀教版数学九年级上册24.2.5 因式分解法 课件(26张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-03 16:52:00 | ||
图片预览








文档简介
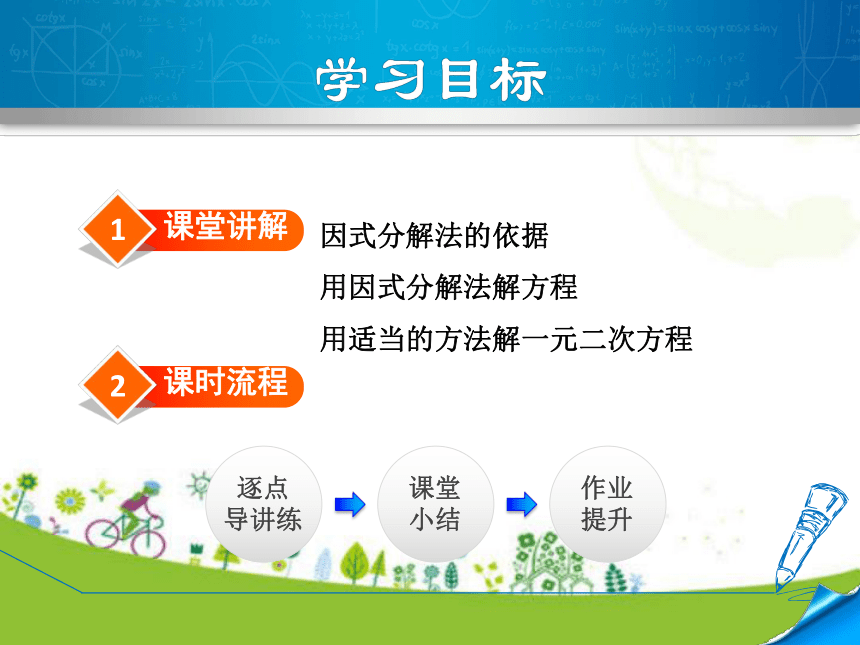
课件26张PPT。24.2 解一元二次方程第5课时 因式分解法冀教版数学九年级上册1课堂讲解因式分解法的依据
用因式分解法解方程
用适当的方法解一元二次方程2课时流程逐点
导讲练课堂小结作业提升解一元二次方程的关键是将它转化为一元一次方程,因此,可将方程的左边分解因式. 于是,得
x(x-2)=0. 所以,x=0,或x-2=0.
方程x2-2x=0的两个根为x1=0,x2=2.对于方程x2-2x=0, 除了可以用配方法或公式法求解,还可以怎样求解呢?
观察和分析小亮的解法,你认为他的解法有没有道理?小亮的思考及解法1知识点因式分解法的依据 小亮的解法是正确的,他给出了解一元二次方
程的又一种方法. 像这 样,把一元二次方程的一
边化为0, 另一边分解成两个一次因式的乘积,进
而转化为两个一元一次方程,从而求出原方程的根,
这种解一元二次方程的 方法叫做因式分解法.知1-讲 因式分解法的依据:
如果a·b=0, 那么a=0或b=0.1我们解一元二次方程3x2-6x=0时,可以运用因式分解法,将此方程化为3x(x-2)=0,从而得到两个一元一次方程3x=0或x-2=0,进而得到原方程的解为x1=0,x2=2.这种解法体现的数学思想是( )
A.转化思想 B.函数思想
C.数形结合思想 D.公理化思想知1-练2用因式分解法解方程,下列过程正确的是( )
A.(2x-3)(3x-4)=0化为2x-3=0或3x-4=0
B.(x+3)(x-1)=1化为x+3=0或x-1=1
C.(x-2)(x-3)=2×3化为x-2=2或x-3=3
D.x(x+2)=0化为x+2=0知1-练2知识点用因式分解法解方程知2-讲因式分解法解一元二次方程的一般步骤:
(1)整理方程,使其右边为0;
(2)将方程左边分解为两个一次式的乘积;
(3)分别令每个一次式为0,得到两个一元一次方程;
(4)分别解这两个一元一次方程,它们的解就是原方
程的解.例1 用因式分解法解下列方程:
(1) 3(x-1)2=2(x-1);
(2) (x+5)2=49.知2-讲解:(1) 原方程可化为 3(x-1)2-2(x-1)=0 ,
(x-1)(3x-5)=0.
得 x-1=0,或3x -5=0,
x1=1,x2= 知2-讲(1) 原方程可化为 (x+5)2-72=0 ,
(x+12)(x-2)=0.
得 x+12=0,或x -2=0,
x1=-12,x2=2. 采用因式分解法解一元二次方程的技巧:
右化零,左分解,两因式,各求解.1用因式分解法解下列方程:
(1) (x+3)(x-2)=0;
4x2-x=0;
(3) (x+3)2=25;
(4) 2(x+1)2+3(x+1)=0.知2-练2已知等腰三角形的腰和底的长分别是一元二次
方程x2-4x+3=0的根,则该三角形的周长可
以是( )
A.5 B.7
C.5或7 D.10知2-练知2-练3△ABC的三边长都是方程x2-6x+8=0的解,则△ABC的周长是( )
A.10
B.12
C.6或10或12
D.6或8或10或123知识点用适当的方法解一元二次方程知3-讲1. 解一元二次方程的方法:
直接开平方法、配方法、公式法、因式分解
法.其中配方法和公式法适合于所有一元二
次方程,直接开方法适合于某些特殊方程.
2.解一元二次方程的基本思路是:
将二次方程化为一次方程,即降次.知3-讲3.解一元二次方程方法的选择顺序:
先特殊后一般,即先考虑直接开平方法和因
式分解法,不能用这两种方法时,再用公式
法;没有特殊要求的,一般不用配方法.例2 用适当的方法解下列一元二次方程:
(1)x2-2x-3=0;
(2)2x2-7x-6=0;
(3)(x-1)2-3(x-1)=0.
导引:方程(1)选择配方法;方程(2)选择公式法;
方程(3)选择因式分解法.知3-讲知3-讲解: (1)x2-2x-3=0,
移项,得x2-2x=3,
配方,得(x-1)2=4,x-1=±2,
∴x1=3,x2=-1.
(2)2x2-7x-6=0,
∵a=2,b=-7,c=-6,
∴Δ=b2-4ac=97>0,知3-讲 (3) (x-1)2-3(x-1)=0,(x-1)(x-1-3)=0,
即(x-1)(x-4)=0.
∴x-1=0,或x-4=0,
∴x1=1,x2=4. 在没有规定方法的前提下解一元二次方程,
首先考虑用因式分解法,其次考虑用公式法.对
于系数较大时,一般不适宜用公式法,如果一次
项系数是偶数,可选用配方法.1解方程(5x-1)2=3(5x-1)的最适当的方法是( )
A.直接开平方法
B.配方法
C.公式法
D.因式分解法知3-练2已知下列方程,请把它们的序号填在相应最适当的解法后的横线上.
①2(x-1)2=6; ②(x-2)2+x2=4;
③(x-2)(x-3)=3; ④x2-2x-1=0;
⑥x2-2x-99=0.
(1) 直接开平方法:________;
(2) 配方法:____________;
(3) 公式法:____________;
(4) 因式分解法:________.知3-练用适当的方法解下列方程:
(1) (x+1)2=9;
(2) x2-4x=6;
(3) 2x2-3x-1=0;
(3) (x-1)2=(2x+1)2.知3-练3解一元二次方程方法的口诀
方程没有一次项,直接开方最理想;
如果缺少常数项,因式分解没商量;
b,c相等都为0,等根是0不要忘;
b,c同时不为0,因式分解或配方,
也可直接套公式,因题而异择良方.完成教材P44习题A组T1-T3;
B组T1-T2
谢谢!
用因式分解法解方程
用适当的方法解一元二次方程2课时流程逐点
导讲练课堂小结作业提升解一元二次方程的关键是将它转化为一元一次方程,因此,可将方程的左边分解因式. 于是,得
x(x-2)=0. 所以,x=0,或x-2=0.
方程x2-2x=0的两个根为x1=0,x2=2.对于方程x2-2x=0, 除了可以用配方法或公式法求解,还可以怎样求解呢?
观察和分析小亮的解法,你认为他的解法有没有道理?小亮的思考及解法1知识点因式分解法的依据 小亮的解法是正确的,他给出了解一元二次方
程的又一种方法. 像这 样,把一元二次方程的一
边化为0, 另一边分解成两个一次因式的乘积,进
而转化为两个一元一次方程,从而求出原方程的根,
这种解一元二次方程的 方法叫做因式分解法.知1-讲 因式分解法的依据:
如果a·b=0, 那么a=0或b=0.1我们解一元二次方程3x2-6x=0时,可以运用因式分解法,将此方程化为3x(x-2)=0,从而得到两个一元一次方程3x=0或x-2=0,进而得到原方程的解为x1=0,x2=2.这种解法体现的数学思想是( )
A.转化思想 B.函数思想
C.数形结合思想 D.公理化思想知1-练2用因式分解法解方程,下列过程正确的是( )
A.(2x-3)(3x-4)=0化为2x-3=0或3x-4=0
B.(x+3)(x-1)=1化为x+3=0或x-1=1
C.(x-2)(x-3)=2×3化为x-2=2或x-3=3
D.x(x+2)=0化为x+2=0知1-练2知识点用因式分解法解方程知2-讲因式分解法解一元二次方程的一般步骤:
(1)整理方程,使其右边为0;
(2)将方程左边分解为两个一次式的乘积;
(3)分别令每个一次式为0,得到两个一元一次方程;
(4)分别解这两个一元一次方程,它们的解就是原方
程的解.例1 用因式分解法解下列方程:
(1) 3(x-1)2=2(x-1);
(2) (x+5)2=49.知2-讲解:(1) 原方程可化为 3(x-1)2-2(x-1)=0 ,
(x-1)(3x-5)=0.
得 x-1=0,或3x -5=0,
x1=1,x2= 知2-讲(1) 原方程可化为 (x+5)2-72=0 ,
(x+12)(x-2)=0.
得 x+12=0,或x -2=0,
x1=-12,x2=2. 采用因式分解法解一元二次方程的技巧:
右化零,左分解,两因式,各求解.1用因式分解法解下列方程:
(1) (x+3)(x-2)=0;
4x2-x=0;
(3) (x+3)2=25;
(4) 2(x+1)2+3(x+1)=0.知2-练2已知等腰三角形的腰和底的长分别是一元二次
方程x2-4x+3=0的根,则该三角形的周长可
以是( )
A.5 B.7
C.5或7 D.10知2-练知2-练3△ABC的三边长都是方程x2-6x+8=0的解,则△ABC的周长是( )
A.10
B.12
C.6或10或12
D.6或8或10或123知识点用适当的方法解一元二次方程知3-讲1. 解一元二次方程的方法:
直接开平方法、配方法、公式法、因式分解
法.其中配方法和公式法适合于所有一元二
次方程,直接开方法适合于某些特殊方程.
2.解一元二次方程的基本思路是:
将二次方程化为一次方程,即降次.知3-讲3.解一元二次方程方法的选择顺序:
先特殊后一般,即先考虑直接开平方法和因
式分解法,不能用这两种方法时,再用公式
法;没有特殊要求的,一般不用配方法.例2 用适当的方法解下列一元二次方程:
(1)x2-2x-3=0;
(2)2x2-7x-6=0;
(3)(x-1)2-3(x-1)=0.
导引:方程(1)选择配方法;方程(2)选择公式法;
方程(3)选择因式分解法.知3-讲知3-讲解: (1)x2-2x-3=0,
移项,得x2-2x=3,
配方,得(x-1)2=4,x-1=±2,
∴x1=3,x2=-1.
(2)2x2-7x-6=0,
∵a=2,b=-7,c=-6,
∴Δ=b2-4ac=97>0,知3-讲 (3) (x-1)2-3(x-1)=0,(x-1)(x-1-3)=0,
即(x-1)(x-4)=0.
∴x-1=0,或x-4=0,
∴x1=1,x2=4. 在没有规定方法的前提下解一元二次方程,
首先考虑用因式分解法,其次考虑用公式法.对
于系数较大时,一般不适宜用公式法,如果一次
项系数是偶数,可选用配方法.1解方程(5x-1)2=3(5x-1)的最适当的方法是( )
A.直接开平方法
B.配方法
C.公式法
D.因式分解法知3-练2已知下列方程,请把它们的序号填在相应最适当的解法后的横线上.
①2(x-1)2=6; ②(x-2)2+x2=4;
③(x-2)(x-3)=3; ④x2-2x-1=0;
⑥x2-2x-99=0.
(1) 直接开平方法:________;
(2) 配方法:____________;
(3) 公式法:____________;
(4) 因式分解法:________.知3-练用适当的方法解下列方程:
(1) (x+1)2=9;
(2) x2-4x=6;
(3) 2x2-3x-1=0;
(3) (x-1)2=(2x+1)2.知3-练3解一元二次方程方法的口诀
方程没有一次项,直接开方最理想;
如果缺少常数项,因式分解没商量;
b,c相等都为0,等根是0不要忘;
b,c同时不为0,因式分解或配方,
也可直接套公式,因题而异择良方.完成教材P44习题A组T1-T3;
B组T1-T2
谢谢!
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
