华东师大版七年级数学下册10.1.1生活中的轴对称(二)教案
文档属性
| 名称 | 华东师大版七年级数学下册10.1.1生活中的轴对称(二)教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 554.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-04 00:00:00 | ||
图片预览

文档简介
10.1.1生活中的轴对称(二)
知识技能目标
1.使学生能够分清轴对称图形和两个图形成轴对称这两个概念的区别和联系;
2.使学生能正确理解关于某条直线成轴对称的两个图形的基本特征.
过程性目标
在探索轴对称图形的过程中,感受蕴藏在图形中的基本特征,并使学生能正确区分图形之间的内在关系.
情感态度目标
在探索轴对称图形的过程中,感受现实生活中处处充满着对称美.
重点和难点
重点:轴对称图形的对应线段相等,对应角相等.
难点:两个图形成轴对称与轴对称图形两个概念的区别与联系.
教学过程
一、创设情境
小实验:给学生每人发一张白纸,在纸的一侧上滴几滴墨水,将纸迅速对折、压平,并用手指压出清晰的折痕,再将纸打开后铺平,观察所得到的图案,位于折痕两侧墨水图案彼此之间有什么关系?它的对称轴是什么呢?
二、探究归纳
如图,
经观察学生不难发现:位于折痕两侧墨水图案完全重合.对称轴为折痕所在直线.
当然象这样的例子还很多. (如下图)
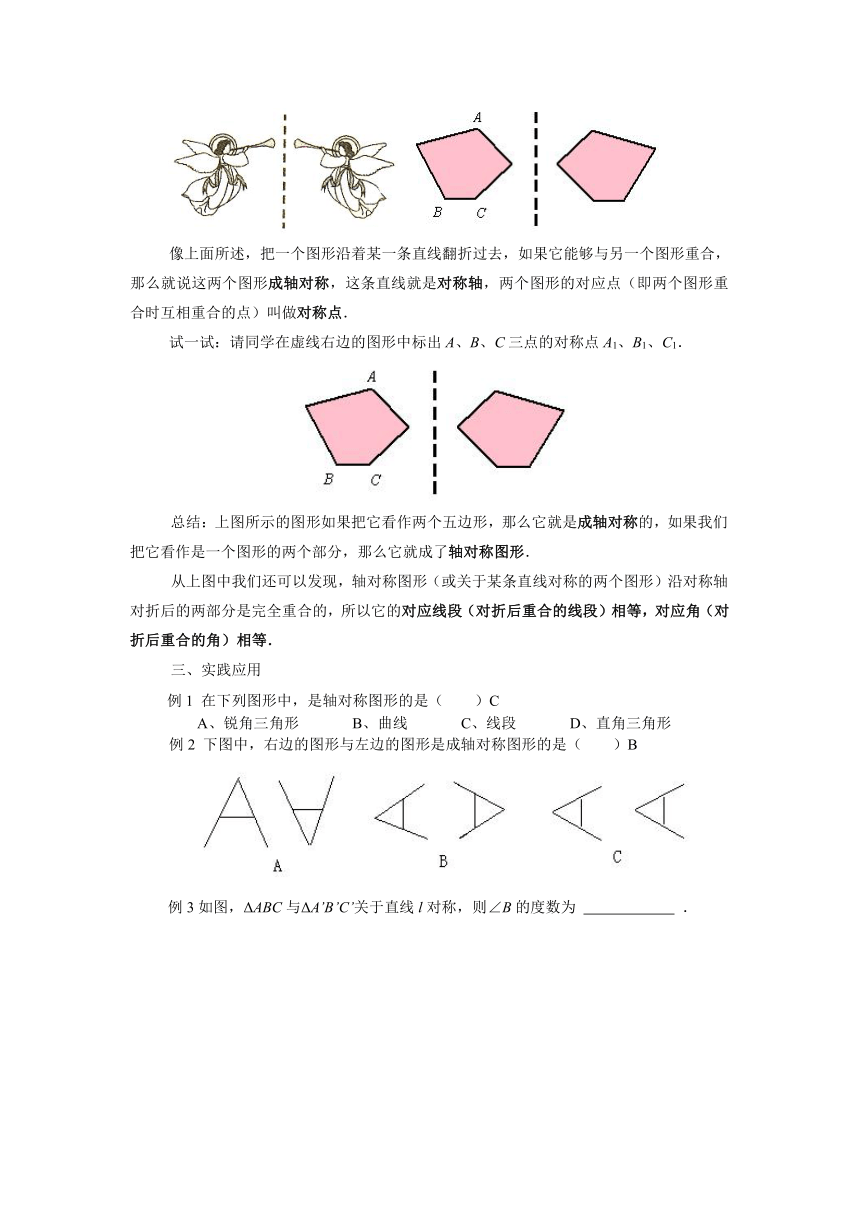
像上面所述,把一个图形沿着某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形成轴对称,这条直线就是对称轴,两个图形的对应点(即两个图形重合时互相重合的点)叫做对称点.
试一试:请同学在虚线右边的图形中标出A、B、C三点的对称点A1、B1、C1.
总结:上图所示的图形如果把它看作两个五边形,那么它就是成轴对称的,如果我们把它看作是一个图形的两个部分,那么它就成了轴对称图形.
从上图中我们还可以发现,轴对称图形(或关于某条直线对称的两个图形)沿对称轴对折后的两部分是完全重合的,所以它的对应线段(对折后重合的线段)相等,对应角(对折后重合的角)相等.
三、实践应用
例1 在下列图形中,是轴对称图形的是( )C
A、锐角三角形 B、曲线 C、线段 D、直角三角形
例2 下图中,右边的图形与左边的图形是成轴对称图形的是( )B
例3如图,ΔABC与ΔA’B’C’关于直线l对称,则∠B的度数为 .
答案:100°. 如果两个图形是关于某条直线成轴对称,那么,这两个图形是全等的,由此,可以得到∠A=∠=50°,∠C=∠=30°,∠B=∠=180°-50°-30°=100°.
例4已知直线l和l外一个点A,画出点A关于l的对称点A/的步骤是:
(1)作射线AN________l,O为垂足;
(2)在射线ON上截取________,则________是点A关于直线l的对应点.
答案:⊥,OA/=OA,点A/
例5如图所示三角形ABC沿直线MN对折后能与三角形A1B1C1重合,试找出A、B、C三点的对称点,哪些线段相等.
四、交流反思
两个图形成轴对称与轴对称图形的概念是既有区别又有联系的.它们的区别在于成轴对称图形是两个图形,而轴对称图形是一个图形,如果把成轴对称图形的两个图形看成一个整体,那么它就成了轴对称图形.它们的共同点是它们对折以后都能重合,对应线段都相等,对应角也相等.
五、检测反馈
1.在下图中标出A、B、C三点的关于直线l对称点A1、B1、C1.
2.下面哪一个选项的右边图形与左边图形成轴对称.
3.在图形中标出点A、B和点C关于直线l的对称点.
