华东师大版七年级数学下册 第10章 10.1.3画轴对称图形 一课一测(含答案)
文档属性
| 名称 | 华东师大版七年级数学下册 第10章 10.1.3画轴对称图形 一课一测(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 185.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-03 00:00:00 | ||
图片预览

文档简介
10.1.3画轴对称图形
A组
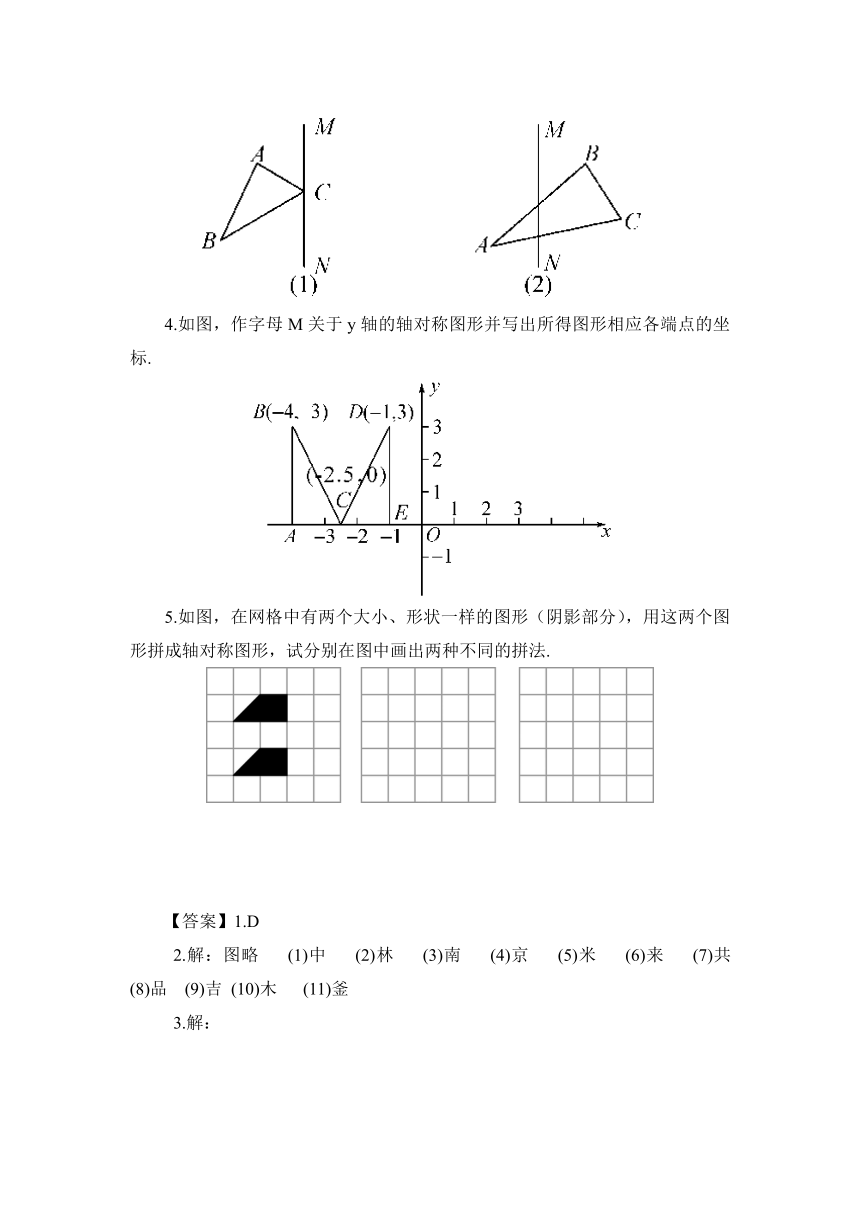
1.已知△ABC 在直角坐标系中的位置如图所示,如果△A′B′C′与△ABC关于y轴对称,那么点A的对应点A′的坐标为( )
A.(-4,2) B.(-4,-2) C.(4,-2) D.(4,2)
2.下列各图都是一个汉字的一半,你能想像出它的另一半并能确定它是什么字吗?(有几个字的笔划在对称轴上.)
3.如图,已知△ABC和直线MN.求作:△A′B′C′,使△A′B′C′和△ABC关于直线MN对称.
4.如图,作字母M关于y轴的轴对称图形并写出所得图形相应各端点的坐标.
5.如图,在网格中有两个大小、形状一样的图形(阴影部分),用这两个图形拼成轴对称图形,试分别在图中画出两种不同的拼法.
【答案】1.D
2.解:图略 (1)中 (2)林 (3)南 (4)京 (5)米 (6)来 (7)共 (8)品 (9)吉 (10)木 (11)釜
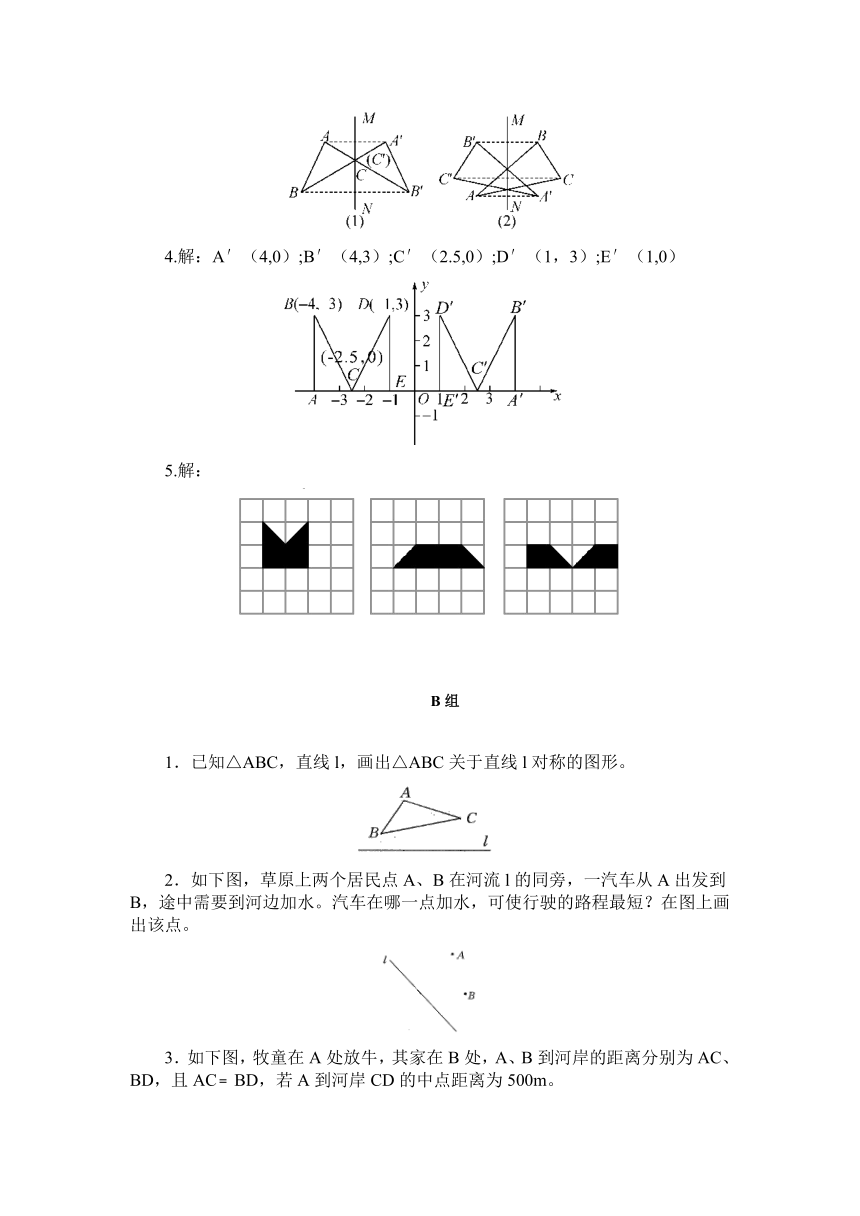
3.解:
4.解:A′(4,0);B′(4,3);C′(2.5,0);D′(1,3);E′(1,0)
5.解:
B组
1.已知△ABC,直线l,画出△ABC关于直线l对称的图形。
2.如下图,草原上两个居民点A、B在河流l的同旁,一汽车从A出发到B,途中需要到河边加水。汽车在哪一点加水,可使行驶的路程最短?在图上画出该点。
3.如下图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,且AC﹦BD,若A到河岸CD的中点距离为500m。
(1)牧童从A处把牛牵到河边饮水后再回家,试问在何处饮水,所走路程最短?在图中作出该处,并说明理由;
(2)最短路程是多少?
答案
1.分析:如果图形是由直线、线段或射线组成时,那么在画出它关于某一条一直线对称的图形时,只要画出图形中的特殊点(如线段的端点、角的顶点等)的对称点,然后连结对称点,就可以画出关于这条直线的对称图形。
解:如下图,我们可以按这样的步骤来画:
(1)画出A、B和C关于直线l的对称点A1、B1、和C1;
(2)连结A1 B1、A1 C1、B1 C1,△A1 B1 C1就是△ABC关于直线l对称的三角形。
方法技巧:画已知图形关于某直线的对称图形,要使①对称轴是对应点连线的垂直平分线;②若它们对应线段或延长相交,则交点必在对称轴上。
2.分析:先将问题抽象为:河流为直线l,在直线l同侧有两个点A和B,在l上找一点使得到A、B两点距离之和最小,然后通过以前学习的几何知识加以解决。
解:如上图,作B点关于直线l的对称点B′,连结A B′与l相交于C,则C点即为所求。
事实上,如果是C′点的话,则连结A C′与C′B和C′B′,
由轴对称性知道,C′B﹦C′B′,CB﹦C B′,
所以C′ 到A、B距离之和A C′﹢CB﹦A C′﹢C′B′,
而C到A、B距离之和AC﹢CB﹦AC﹢C B′﹦A B′。
在△A C′B′中,三角形两边之和大于第三边A C′﹢C′B′>A B′,
所以C点为所求的点。
方法技巧:根据轴对称,把l同侧两点转化为异侧两点,根据“三角形两边之和大于第三边”这个结论,得到答案。
3.错误解法:(1)作AC⊥CD于C,连结BC,C点为所求点。
(2)作BD⊥CD于D,连结AD,D点为所求点。
误区分析:把画“对称点”和“点到直线的距离”混淆。
正确解答:(1)已知直线CD和CD同侧两点A、B。求作:CD上一点M,使AM﹢BM最小。
作法:①作点A关于CD的对称点A′;
②连结A′B交CD于点M,则点M即为所求的点。
证明:在CD上任取一点M′,连结A M′、A M′、BM′、AM,
∵直线CD是A、A′的对称轴,M M′在CD上,
∴AM﹦A′M,A M′﹦A′M′
∴AM﹢BM﹦A′M﹢BM﹦A′B。
在△ABC中,∵A′M′﹢BM′>A′B ,
∴A′M′﹢BM′>AM﹢BM,即AM﹢BM最小。
(2)由(1)可得:AM﹦A′M,A′C﹦AC﹦BD,
∴△ A′CM≌△BDM,∴A′M,﹦BM,CM﹦DM,
即M为CD的中点,且A′B﹦2AM。
∵AM﹦500m,
∴A′B﹦AM﹢BM﹦2AM﹦1000m。
∴最短路程为1000m。
