江苏省常熟市王淦昌中学2019-2020学年高一下学期开学考试数学试卷(word版含答案)
文档属性
| 名称 | 江苏省常熟市王淦昌中学2019-2020学年高一下学期开学考试数学试卷(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 610.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-04 00:00:00 | ||
图片预览



文档简介
王淦昌中学2019-2020学年高一下学期开学考试
数学试卷
一.选择题:(12*5=60分)
1.直线的斜率为( )
A. B. C. D.
2.某公司生产甲、乙、丙三种型号的吊车,产量分别为 120 台,600 台和 200 台,为检验该 公司的产品质量,现用分层抽样的方法抽取 46 台进行检验,则抽到乙种型号的吊车有 ( )
A.6 台 B.10 台 C.20 台 D.30 台
3. 已知角满足,则( )
A. B. C. D.
4.在锐角△ABC中,角A,B所对的边分别为a,b.若2asinB=b,则角A等于( )
A. B. C. D.
5.若直线与直线平行,则等于( )
A.-1或2 B.-1 C.2 D.
6.某公司10位员工的月工资(单位:元)为,其均值和方差分别为和,若从下月开始每位员工的月工资增加100元,则这10位员工下月工资的均值和方差分别
为 ( )
A. , B. , C. , D. ,
7.一艘海轮从A处出发,以每小时40海里的速度沿南偏东40°的 方向直线航行,30分钟后到达B处,在C处有一座灯塔,海轮在A处观察灯塔,其方向是南偏东70°,在B处观察灯塔,其方向是北偏东65°,那么B,C两点间的距离是 ( )
A. B. C. D.
8.若P(3,1)为圆的弦AB的中点,则直线AB的方程是( )
A. B. C. D.
9.已知圆M与直线及都相切,圆心在直线上,则
圆的方程为 ( )
A. B.
C. D.
10. 已知点是直线上一动点,直线是圆的
两条切线,为切点,为圆心,则四边形面积的最小值是 ( )
A. B. C. D.
11.在中,已知的平分线,则的面积( )
A. B. C. D.
12.已知点,点是圆上的动点,点是圆上的动点,则的最大值为( )
A. B. C. D.
二.填空题:(4*5=20分)
13.过点(1,3)且在两坐标轴上截距相等的直线方程为
14.一个社会调查机构就某地居民收入调查了10000人,并根据所得数据画出了如图所示的频率分布直方图,现要从这10000人中再用分层抽样的方法抽出100人作进一步调查,则月收入在[2500,3000)(元)内的应抽出 人.
15.已知,则 .
16. 已知直线l1:与l2:相交于点P,线段AB是圆
C:的一条动弦,且AB=,则的最小值是
3. 解答题:(10+12+12+12+12+12=70分)
17.(本题满分10分)
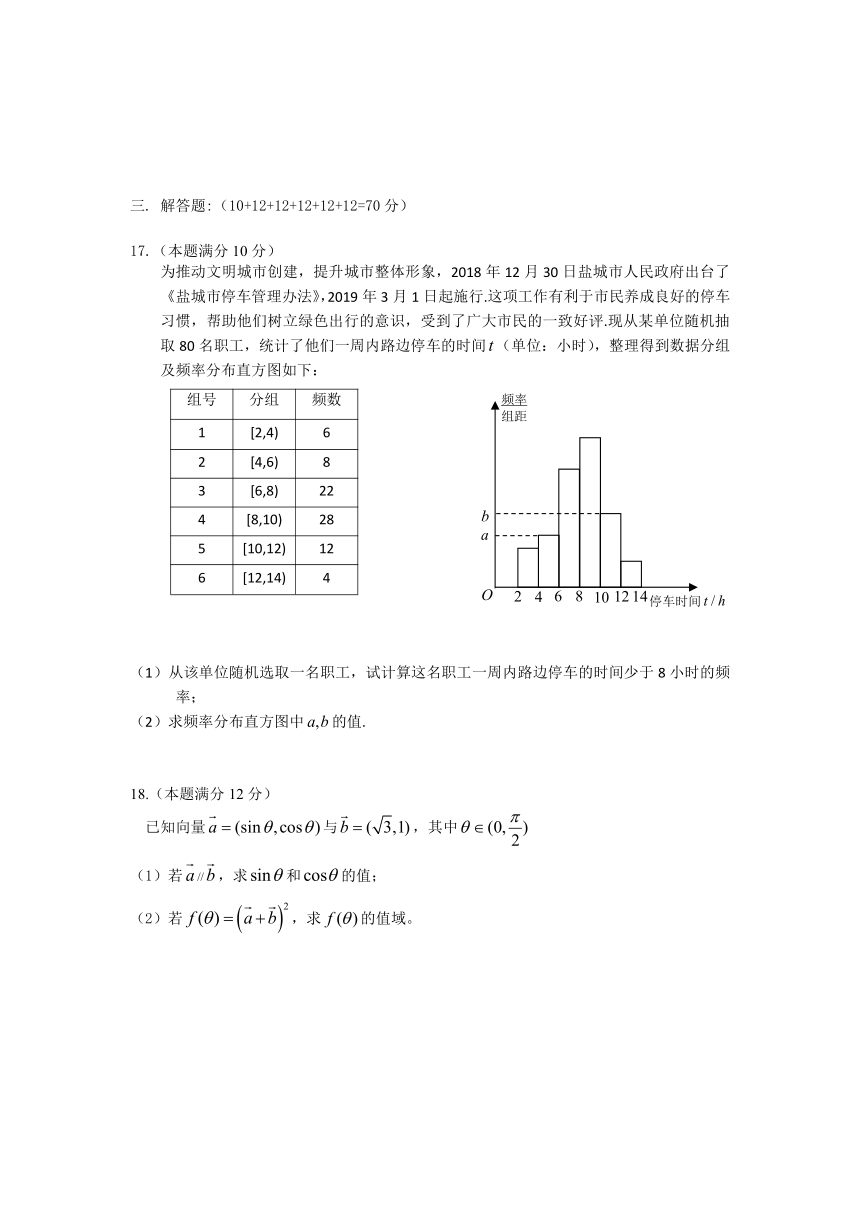
为推动文明城市创建,提升城市整体形象,2018年12月30日盐城市人民政府出台了《盐城市停车管理办法》,2019年3月1日起施行.这项工作有利于市民养成良好的停车习惯,帮助他们树立绿色出行的意识,受到了广大市民的一致好评.现从某单位随机抽取80名职工,统计了他们一周内路边停车的时间(单位:小时),整理得到数据分组及频率分布直方图如下:
组号 分组 频数
1 [2,4) 6
2 [4,6) 8
3 [6,8) 22
4 [8,10) 28
5 [10,12) 12
6 [12,14) 4
(1)从该单位随机选取一名职工,试计算这名职工一周内路边停车的时间少于8小时的频率;
(2)求频率分布直方图中的值.
18.(本题满分12分)
已知向量与,其中
(1)若,求和的值;
(2)若,求的值域。
19.(本题满分12分)
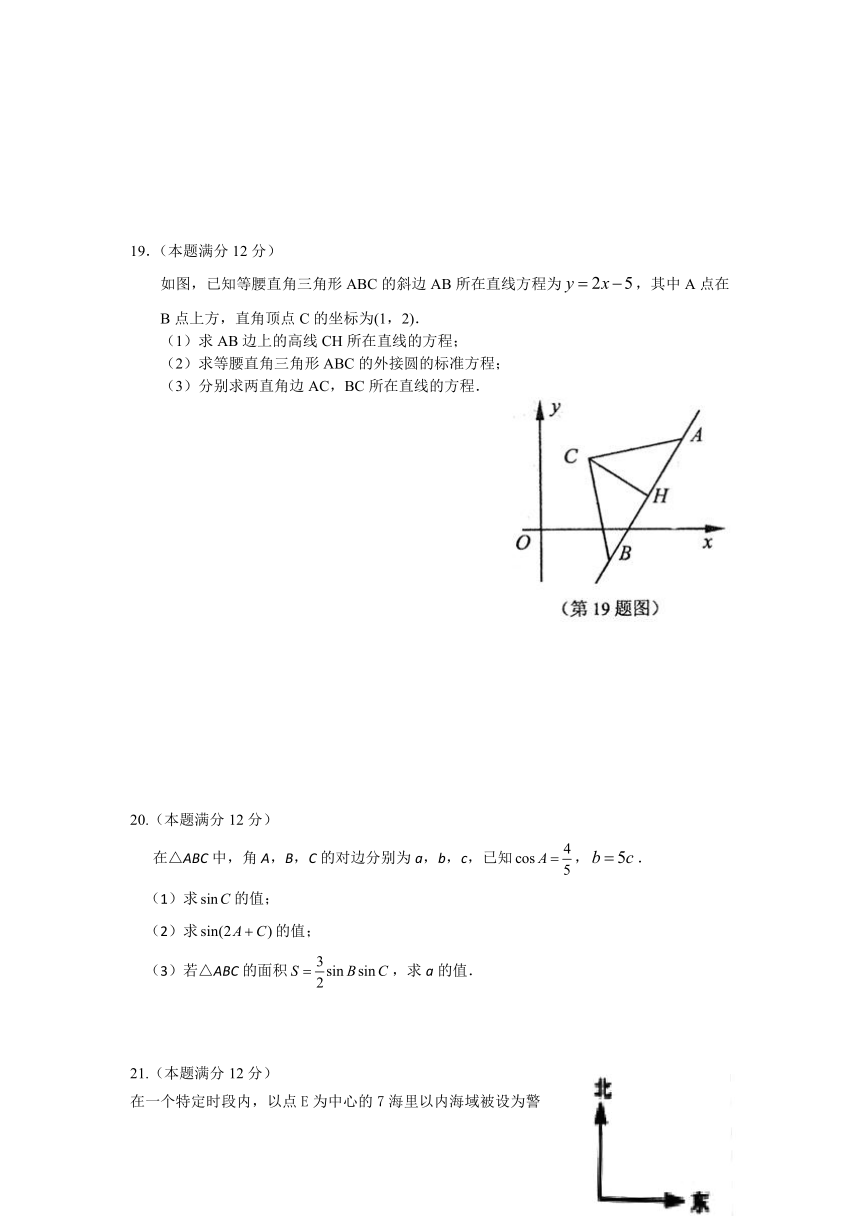
如图,已知等腰直角三角形ABC的斜边AB所在直线方程为,其中A点在B点上方,直角顶点C的坐标为(1,2).
(1)求AB边上的高线CH所在直线的方程;
(2)求等腰直角三角形ABC的外接圆的标准方程;
(3)分别求两直角边AC,BC所在直线的方程.
20.(本题满分12分)
在△ABC中,角A,B,C的对边分别为a,b,c,已知,.
(1)求的值;
(2)求的值;
(3)若△ABC的面积,求a的值.
21.(本题满分12分)
在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东且与点A相距40海里的位置B,经过40分钟又测得该船已行驶到点A北偏东+(其中sin=,)且与点A相距10海里的位置C.
(1)求该船的行驶速度(单位:海里/时);
(2)若该船不改变航行方向继续行驶.
判断它是否会进入警戒水域,并说明理由.
22.(本题满分12分)
已知圆C经过A(﹣2,0),B(1,)两点,且圆心C在直线l1:y=x上.
(1)求圆C的方程;
(2)已知过点P(1,2)的直线l2与圆C相交截得的弦长为,求直线l2的方程;
(3)已知点M(1,1),在平面内是否存在异于点M的定点N,对于圆C上的任意动点Q,都有为定值?若存在求出定点N的坐标,若不存在说明理由.
高一数学开学考试试卷答案
一.选择题
DDDDBD ADCADD
二.填空题
13. y=3x或y=-x+4
14. 25
15.
16.
三.解答题
17. 解:(1) 所求频率为 ……………4分
(2), ……………7分
…………… 10分
(说明:本题只要答案对就算正确)
18.解:(1) 求得
又 , ------4分
(注:本问也可以结合或利用来求解)
(2)
---------7分
又,,-------10分
,即函数的值域为-----------12分
20.解:(1) ∵==,
∴. …………………………………1分
∵,, ∴.
∵,
∴==. ……………………………4分
(2)∵,∴为锐角,
∴.
∵,
, ………………………6分
∴=
=. ………………………8分
(3)∵, ∴,.
∴. ……………10分
又∵S=,
∴, ∴. ……………………12分
21.解 (1)如图,AB=40,AC=10,
由于0<<,所以cos=……………………2分
由余弦定理得BC=……………4分
所以船的行驶速度为(海里/小时). ……………………5分
(2)解法一 如图所示,以A为原点建立平面直角坐标系,设点B、C的坐标分别是
B(x1,y2), C(x1,y2),BC与x轴的交点为D.
由题设有,x1=y1= AB=40, ……7分
x2=ACcos.
……9分
所以过点B、C的直线l的斜率k=,直线l的方程为y=2x-40.
又点E(0,-55)到直线l的距离d=……11 分
所以船会进入警戒水域. ……………………………12 分
解法二 如图所示,设直线AE与BC的延长线相交于点Q.在△ABC中,
由余弦定理得,
===.…………6 分
从而
在中,由正弦定理得,
AQ=…………8分
由于AE=55>40=AQ,所以点Q位于点A和点E之间,且QE=AE-AQ=15.过点E作EPBC于点P,则EP为点E到直线BC的距离.在Rt中,
PE=QE·sin
= ……………………11 分
所以船会进入警戒水域. ………………………12 分
停车时间
频率
组距
数学试卷
一.选择题:(12*5=60分)
1.直线的斜率为( )
A. B. C. D.
2.某公司生产甲、乙、丙三种型号的吊车,产量分别为 120 台,600 台和 200 台,为检验该 公司的产品质量,现用分层抽样的方法抽取 46 台进行检验,则抽到乙种型号的吊车有 ( )
A.6 台 B.10 台 C.20 台 D.30 台
3. 已知角满足,则( )
A. B. C. D.
4.在锐角△ABC中,角A,B所对的边分别为a,b.若2asinB=b,则角A等于( )
A. B. C. D.
5.若直线与直线平行,则等于( )
A.-1或2 B.-1 C.2 D.
6.某公司10位员工的月工资(单位:元)为,其均值和方差分别为和,若从下月开始每位员工的月工资增加100元,则这10位员工下月工资的均值和方差分别
为 ( )
A. , B. , C. , D. ,
7.一艘海轮从A处出发,以每小时40海里的速度沿南偏东40°的 方向直线航行,30分钟后到达B处,在C处有一座灯塔,海轮在A处观察灯塔,其方向是南偏东70°,在B处观察灯塔,其方向是北偏东65°,那么B,C两点间的距离是 ( )
A. B. C. D.
8.若P(3,1)为圆的弦AB的中点,则直线AB的方程是( )
A. B. C. D.
9.已知圆M与直线及都相切,圆心在直线上,则
圆的方程为 ( )
A. B.
C. D.
10. 已知点是直线上一动点,直线是圆的
两条切线,为切点,为圆心,则四边形面积的最小值是 ( )
A. B. C. D.
11.在中,已知的平分线,则的面积( )
A. B. C. D.
12.已知点,点是圆上的动点,点是圆上的动点,则的最大值为( )
A. B. C. D.
二.填空题:(4*5=20分)
13.过点(1,3)且在两坐标轴上截距相等的直线方程为
14.一个社会调查机构就某地居民收入调查了10000人,并根据所得数据画出了如图所示的频率分布直方图,现要从这10000人中再用分层抽样的方法抽出100人作进一步调查,则月收入在[2500,3000)(元)内的应抽出 人.
15.已知,则 .
16. 已知直线l1:与l2:相交于点P,线段AB是圆
C:的一条动弦,且AB=,则的最小值是
3. 解答题:(10+12+12+12+12+12=70分)
17.(本题满分10分)
为推动文明城市创建,提升城市整体形象,2018年12月30日盐城市人民政府出台了《盐城市停车管理办法》,2019年3月1日起施行.这项工作有利于市民养成良好的停车习惯,帮助他们树立绿色出行的意识,受到了广大市民的一致好评.现从某单位随机抽取80名职工,统计了他们一周内路边停车的时间(单位:小时),整理得到数据分组及频率分布直方图如下:
组号 分组 频数
1 [2,4) 6
2 [4,6) 8
3 [6,8) 22
4 [8,10) 28
5 [10,12) 12
6 [12,14) 4
(1)从该单位随机选取一名职工,试计算这名职工一周内路边停车的时间少于8小时的频率;
(2)求频率分布直方图中的值.
18.(本题满分12分)
已知向量与,其中
(1)若,求和的值;
(2)若,求的值域。
19.(本题满分12分)
如图,已知等腰直角三角形ABC的斜边AB所在直线方程为,其中A点在B点上方,直角顶点C的坐标为(1,2).
(1)求AB边上的高线CH所在直线的方程;
(2)求等腰直角三角形ABC的外接圆的标准方程;
(3)分别求两直角边AC,BC所在直线的方程.
20.(本题满分12分)
在△ABC中,角A,B,C的对边分别为a,b,c,已知,.
(1)求的值;
(2)求的值;
(3)若△ABC的面积,求a的值.
21.(本题满分12分)
在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东且与点A相距40海里的位置B,经过40分钟又测得该船已行驶到点A北偏东+(其中sin=,)且与点A相距10海里的位置C.
(1)求该船的行驶速度(单位:海里/时);
(2)若该船不改变航行方向继续行驶.
判断它是否会进入警戒水域,并说明理由.
22.(本题满分12分)
已知圆C经过A(﹣2,0),B(1,)两点,且圆心C在直线l1:y=x上.
(1)求圆C的方程;
(2)已知过点P(1,2)的直线l2与圆C相交截得的弦长为,求直线l2的方程;
(3)已知点M(1,1),在平面内是否存在异于点M的定点N,对于圆C上的任意动点Q,都有为定值?若存在求出定点N的坐标,若不存在说明理由.
高一数学开学考试试卷答案
一.选择题
DDDDBD ADCADD
二.填空题
13. y=3x或y=-x+4
14. 25
15.
16.
三.解答题
17. 解:(1) 所求频率为 ……………4分
(2), ……………7分
…………… 10分
(说明:本题只要答案对就算正确)
18.解:(1) 求得
又 , ------4分
(注:本问也可以结合或利用来求解)
(2)
---------7分
又,,-------10分
,即函数的值域为-----------12分
20.解:(1) ∵==,
∴. …………………………………1分
∵,, ∴.
∵,
∴==. ……………………………4分
(2)∵,∴为锐角,
∴.
∵,
, ………………………6分
∴=
=. ………………………8分
(3)∵, ∴,.
∴. ……………10分
又∵S=,
∴, ∴. ……………………12分
21.解 (1)如图,AB=40,AC=10,
由于0<<,所以cos=……………………2分
由余弦定理得BC=……………4分
所以船的行驶速度为(海里/小时). ……………………5分
(2)解法一 如图所示,以A为原点建立平面直角坐标系,设点B、C的坐标分别是
B(x1,y2), C(x1,y2),BC与x轴的交点为D.
由题设有,x1=y1= AB=40, ……7分
x2=ACcos.
……9分
所以过点B、C的直线l的斜率k=,直线l的方程为y=2x-40.
又点E(0,-55)到直线l的距离d=……11 分
所以船会进入警戒水域. ……………………………12 分
解法二 如图所示,设直线AE与BC的延长线相交于点Q.在△ABC中,
由余弦定理得,
===.…………6 分
从而
在中,由正弦定理得,
AQ=…………8分
由于AE=55>40=AQ,所以点Q位于点A和点E之间,且QE=AE-AQ=15.过点E作EPBC于点P,则EP为点E到直线BC的距离.在Rt中,
PE=QE·sin
= ……………………11 分
所以船会进入警戒水域. ………………………12 分
停车时间
频率
组距
同课章节目录
