黑龙江省哈尔滨哈十七中学2019-2020学年第二学期九年级数学线上学习检测
文档属性
| 名称 | 黑龙江省哈尔滨哈十七中学2019-2020学年第二学期九年级数学线上学习检测 |

|
|
| 格式 | |||
| 文件大小 | 465.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 1970-01-01 08:00:00 | ||
图片预览

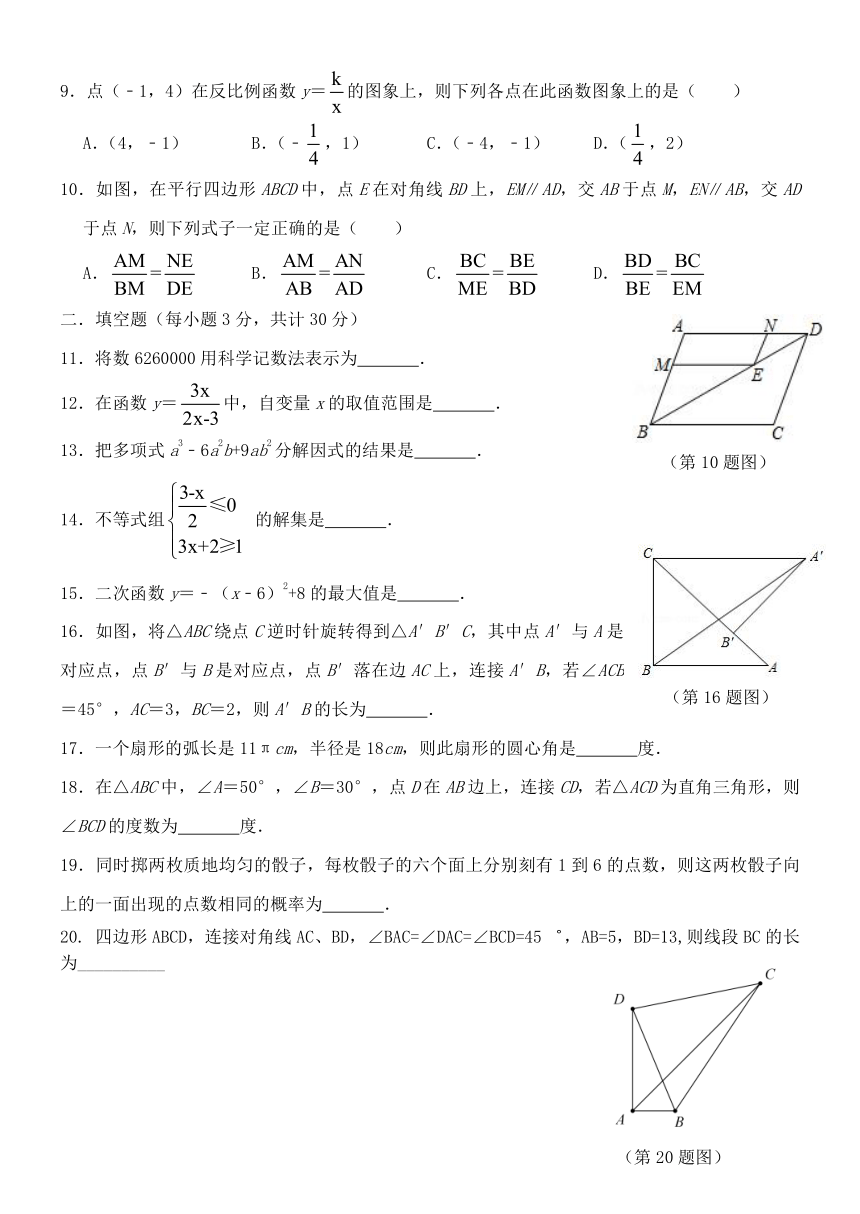
文档简介
哈十七中学初四学年2020年寒假学情检测
一.选择题(每小题3分,共计30分)
1.﹣9的相反数是( )
1 1
A.﹣9 B.﹣ C.9 D.
9 9
2.下列运算一定正确的是( )
2 2 3 6
A.2a+2a=2a B.a?a=a
2 3 6 2 2
C.(2a) =6a D.(a+b)(a﹣b)=a﹣b
3.下列汽车标志中,可以看作是中心对称图形的是 ( )
A. B. C. D.
4.七个大小相同的正方体搭成的几何体如图所示,其左视图是( ) (第4题图)
A. B. C. D.
5.如图,PA、PB分别与⊙O相切于A、B两点,点C为⊙O上一点,
连接AC、BC,若∠P=50°,则∠ACB的度数为( )
A.60° B.75° C.70° D.65° (第5题图)
2
6.将抛物线y=2x向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为( )
2 2 2 2
A.y=2(x+2)+3 B.y=2(x﹣2)+3 C.y=2(x﹣2) ﹣3 D.y=2(x+2)﹣3
7.某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率
为( )
A.20% B.40% C.18% D.36%
2 3
8.方程 = 的解为( )
3x-1 x
3 11 3 7
A.x= B.x= C.x= D.x=
11 3 7 3
k
9.点(﹣1,4)在反比例函数y= 的图象上,则下列各点在此函数图象上的是( )
x
1 1
A.(4,﹣1) B.(﹣ ,1) C.(﹣4,﹣1) D.( ,2)
4 4
10.如图,在平行四边形ABCD中,点E在对角线BD上,EM∥AD,交AB于点M,EN∥AB,交AD
于点N,则下列式子一定正确的是( )
AM NE AM AN BC BE BD BC
A. = B. = C. = D. =
BM DE AB AD ME BD BE EM
二.填空题(每小题3分,共计30分)
11.将数6260000用科学记数法表示为 .
3x
12.在函数y= 中,自变量x的取值范围是 .
2x-3
3 2 2
13.把多项式a﹣6ab+9ab分解因式的结果是 . (第10题图)
?3-x
? ≤0
14.不等式组? 2 的解集是 .
??3x+2≥1
2
15.二次函数y=﹣(x﹣6)+8的最大值是 .
16.如图,将△ABC绕点C逆时针旋转得到△A′B′C,其中点A′与A是
对应点,点B′与B是对应点,点B′落在边AC上,连接A′B,若∠ACB
(第16题图)
=45°,AC=3,BC=2,则A′B的长为 .
17.一个扇形的弧长是11πcm,半径是18cm,则此扇形的圆心角是 度.
18.在△ABC中,∠A=50°,∠B=30°,点D在AB边上,连接CD,若△ACD为直角三角形,则
∠BCD的度数为 度.
19.同时掷两枚质地均匀的骰子,每枚骰子的六个面上分别刻有1到6的点数,则这两枚骰子向
上的一面出现的点数相同的概率为 .
20. 四边形ABCD,连接对角线AC、BD,∠BAC=∠DAC=∠BCD=45゜,AB=5,BD=13,则线段BC的长
为__________
(第20题图)
三、解答题(21-25每题6分、26每题10分,共计40分)
2 2 2
a -b ? 2ab-b ?
21、先化简,再求值 ??a- ?,其中a=2+tan60°,b=4sin30°- ,
? ? 3
a ? a ?
22、如图,在边长为1个单位长度的小正方形组成的12×12网格中,给出了四边形ABCD的两条
边AB与BC,且四边形ABCD是一个轴对称图形,其对称轴为直线AC.
(1)试在图中标出点D,并画出该四边形的另两条边;
(2)将四边形ABCD绕点B逆时针旋转90゜,画出旋转后的
四边形BMNP(A与M对应,D与N对应,C与P对应)
(3)连接DM,并直接写出四边形ADMB的周长
23、为了解某种电动汽车的性能,对这种电动汽车进行了抽检,将一次充电后行驶的里程数分为A,
B,C,D四个等级,其中相应等级的里程依次为200千米,210千米,220千米,230千米,获得
如下不完整的统计图.
电动车一次充电
行驶里程数扇形统计图
根据以上信息,解答下列问题:
(1)问这次被抽检的电动汽车共有几辆?
(2)通过计算,补全条形统计图.
(3)估计这种电动汽车一次充电后行驶的平均里程数为多少千米?
24、春平中学要为学校科技活动小组提供实验器材,计划购买A型、B型两种型号的放大镜,若购
买8个A型放大镜和5个B型放大镜需用220元;若购买4个A型放大镜和6个B型放大镜需用
152元.
(1)求每个A型放大镜和每个B型放大镜各多少元;
(2)春平中学决定购买A型放大镜和B型放大镜共75个,总费用不超过1180元,那么最多
可以购买多少个A型放大镜?
25、如图1,AB是⊙O的直径,弦CD⊥AB于点E,点G是弧AD上一点,AG、CD的延长线交于点F,
连接CG
(1)求证:∠ACG=∠F
(2)如图2,AB与CG交于点P,若∠F=45゜,CP=4,GP=5,求⊙O的半径
(图1) (图2)
26、如图1,直线y=kx+b(k≠0,k、b为常数)交x轴的正半轴于点A(4,0),交y轴正半轴于
1
点B,tan∠ABO=2
(1)求直线AB的解析式
(2)点C是线段AB中点,点P是x轴负半轴上一点,连接PC,设点P的横坐标为t,△APC的面
积为m,求m与t之间的函数关系式(不要求写出自变量的取值范围)
(3)在(2)的条件下,以AP为底作等腰△APM(点M在x轴下方),过点A作直线l∥PM,过点
O作OE⊥AM于E,延长EO交直线l于点F,连接PF、OM,2∠PFO+∠AFE=180゜,△PMO的面积为
2m,求t值
3
(图1) (备用图1)
(备用图2)
一.选择题(每小题3分,共计30分)
1.﹣9的相反数是( )
1 1
A.﹣9 B.﹣ C.9 D.
9 9
2.下列运算一定正确的是( )
2 2 3 6
A.2a+2a=2a B.a?a=a
2 3 6 2 2
C.(2a) =6a D.(a+b)(a﹣b)=a﹣b
3.下列汽车标志中,可以看作是中心对称图形的是 ( )
A. B. C. D.
4.七个大小相同的正方体搭成的几何体如图所示,其左视图是( ) (第4题图)
A. B. C. D.
5.如图,PA、PB分别与⊙O相切于A、B两点,点C为⊙O上一点,
连接AC、BC,若∠P=50°,则∠ACB的度数为( )
A.60° B.75° C.70° D.65° (第5题图)
2
6.将抛物线y=2x向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为( )
2 2 2 2
A.y=2(x+2)+3 B.y=2(x﹣2)+3 C.y=2(x﹣2) ﹣3 D.y=2(x+2)﹣3
7.某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率
为( )
A.20% B.40% C.18% D.36%
2 3
8.方程 = 的解为( )
3x-1 x
3 11 3 7
A.x= B.x= C.x= D.x=
11 3 7 3
k
9.点(﹣1,4)在反比例函数y= 的图象上,则下列各点在此函数图象上的是( )
x
1 1
A.(4,﹣1) B.(﹣ ,1) C.(﹣4,﹣1) D.( ,2)
4 4
10.如图,在平行四边形ABCD中,点E在对角线BD上,EM∥AD,交AB于点M,EN∥AB,交AD
于点N,则下列式子一定正确的是( )
AM NE AM AN BC BE BD BC
A. = B. = C. = D. =
BM DE AB AD ME BD BE EM
二.填空题(每小题3分,共计30分)
11.将数6260000用科学记数法表示为 .
3x
12.在函数y= 中,自变量x的取值范围是 .
2x-3
3 2 2
13.把多项式a﹣6ab+9ab分解因式的结果是 . (第10题图)
?3-x
? ≤0
14.不等式组? 2 的解集是 .
??3x+2≥1
2
15.二次函数y=﹣(x﹣6)+8的最大值是 .
16.如图,将△ABC绕点C逆时针旋转得到△A′B′C,其中点A′与A是
对应点,点B′与B是对应点,点B′落在边AC上,连接A′B,若∠ACB
(第16题图)
=45°,AC=3,BC=2,则A′B的长为 .
17.一个扇形的弧长是11πcm,半径是18cm,则此扇形的圆心角是 度.
18.在△ABC中,∠A=50°,∠B=30°,点D在AB边上,连接CD,若△ACD为直角三角形,则
∠BCD的度数为 度.
19.同时掷两枚质地均匀的骰子,每枚骰子的六个面上分别刻有1到6的点数,则这两枚骰子向
上的一面出现的点数相同的概率为 .
20. 四边形ABCD,连接对角线AC、BD,∠BAC=∠DAC=∠BCD=45゜,AB=5,BD=13,则线段BC的长
为__________
(第20题图)
三、解答题(21-25每题6分、26每题10分,共计40分)
2 2 2
a -b ? 2ab-b ?
21、先化简,再求值 ??a- ?,其中a=2+tan60°,b=4sin30°- ,
? ? 3
a ? a ?
22、如图,在边长为1个单位长度的小正方形组成的12×12网格中,给出了四边形ABCD的两条
边AB与BC,且四边形ABCD是一个轴对称图形,其对称轴为直线AC.
(1)试在图中标出点D,并画出该四边形的另两条边;
(2)将四边形ABCD绕点B逆时针旋转90゜,画出旋转后的
四边形BMNP(A与M对应,D与N对应,C与P对应)
(3)连接DM,并直接写出四边形ADMB的周长
23、为了解某种电动汽车的性能,对这种电动汽车进行了抽检,将一次充电后行驶的里程数分为A,
B,C,D四个等级,其中相应等级的里程依次为200千米,210千米,220千米,230千米,获得
如下不完整的统计图.
电动车一次充电
行驶里程数扇形统计图
根据以上信息,解答下列问题:
(1)问这次被抽检的电动汽车共有几辆?
(2)通过计算,补全条形统计图.
(3)估计这种电动汽车一次充电后行驶的平均里程数为多少千米?
24、春平中学要为学校科技活动小组提供实验器材,计划购买A型、B型两种型号的放大镜,若购
买8个A型放大镜和5个B型放大镜需用220元;若购买4个A型放大镜和6个B型放大镜需用
152元.
(1)求每个A型放大镜和每个B型放大镜各多少元;
(2)春平中学决定购买A型放大镜和B型放大镜共75个,总费用不超过1180元,那么最多
可以购买多少个A型放大镜?
25、如图1,AB是⊙O的直径,弦CD⊥AB于点E,点G是弧AD上一点,AG、CD的延长线交于点F,
连接CG
(1)求证:∠ACG=∠F
(2)如图2,AB与CG交于点P,若∠F=45゜,CP=4,GP=5,求⊙O的半径
(图1) (图2)
26、如图1,直线y=kx+b(k≠0,k、b为常数)交x轴的正半轴于点A(4,0),交y轴正半轴于
1
点B,tan∠ABO=2
(1)求直线AB的解析式
(2)点C是线段AB中点,点P是x轴负半轴上一点,连接PC,设点P的横坐标为t,△APC的面
积为m,求m与t之间的函数关系式(不要求写出自变量的取值范围)
(3)在(2)的条件下,以AP为底作等腰△APM(点M在x轴下方),过点A作直线l∥PM,过点
O作OE⊥AM于E,延长EO交直线l于点F,连接PF、OM,2∠PFO+∠AFE=180゜,△PMO的面积为
2m,求t值
3
(图1) (备用图1)
(备用图2)
同课章节目录
