新版沪科版2019_2020学年九年级数学下册第24章圆24.3圆周角作业设计(含答案)
文档属性
| 名称 | 新版沪科版2019_2020学年九年级数学下册第24章圆24.3圆周角作业设计(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 236.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-04 13:41:37 | ||
图片预览


文档简介
24.3 圆周角
一.选择题(共10小题)
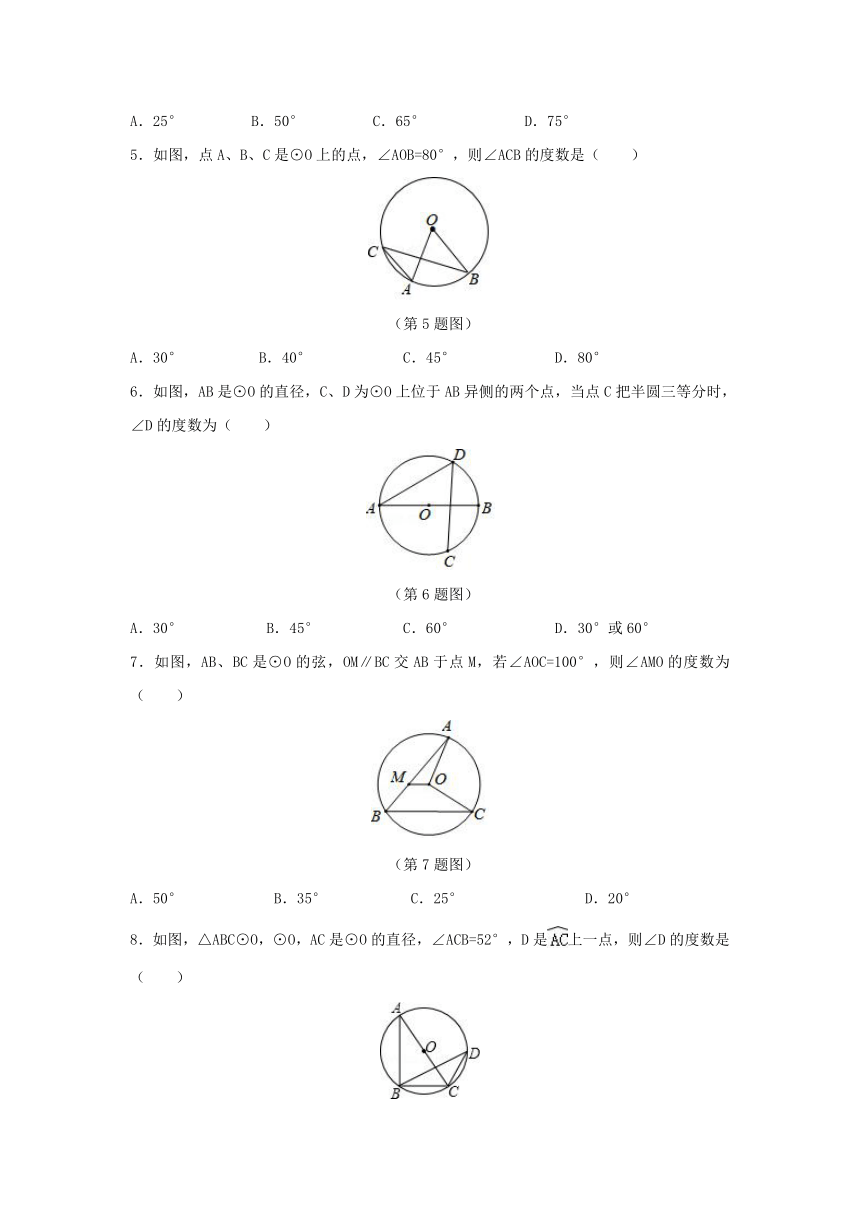
1.如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是( )
(第1题图)
A.50° B.60° C.80° D.100°
2.如图,A、B、C是⊙O上的三点,若∠A+∠C=75°,则∠AOC的度数为( )
(第2题图)
A.150° B.140° C.130° D.120°
3.如图,AB是⊙O的直线,C是⊙O上一点(A、B除外),∠AOD=130°,则∠C的度数是( )
(第3题图)
A.50° B.60° C.25° D.30°
4.如图,已知AB是⊙O的直径,∠CBA=25°,则∠D的度数为( )
(第4题图)
A.25° B.50° C.65° D.75°
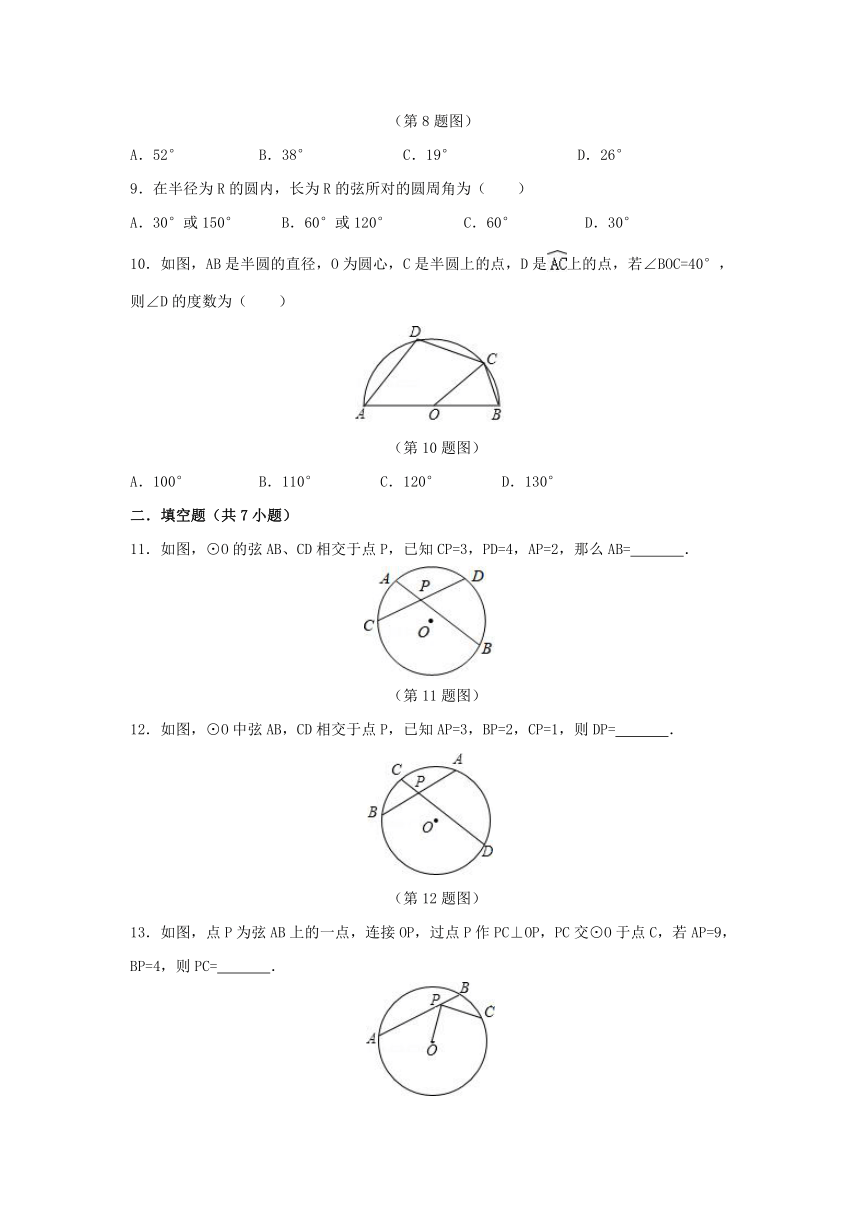
5.如图,点A、B、C是⊙O上的点,∠AOB=80°,则∠ACB的度数是( )
(第5题图)
A.30° B.40° C.45° D.80°
6.如图,AB是⊙O的直径,C、D为⊙O上位于AB异侧的两个点,当点C把半圆三等分时,∠D的度数为( )
(第6题图)
A.30° B.45° C.60° D.30°或60°
7.如图,AB、BC是⊙O的弦,OM∥BC交AB于点M,若∠AOC=100°,则∠AMO的度数为( )
(第7题图)
A.50° B.35° C.25° D.20°
8.如图,△ABC⊙O,⊙O,AC是⊙O的直径,∠ACB=52°,D是上一点,则∠D的度数是( )
(第8题图)
A.52° B.38° C.19° D.26°
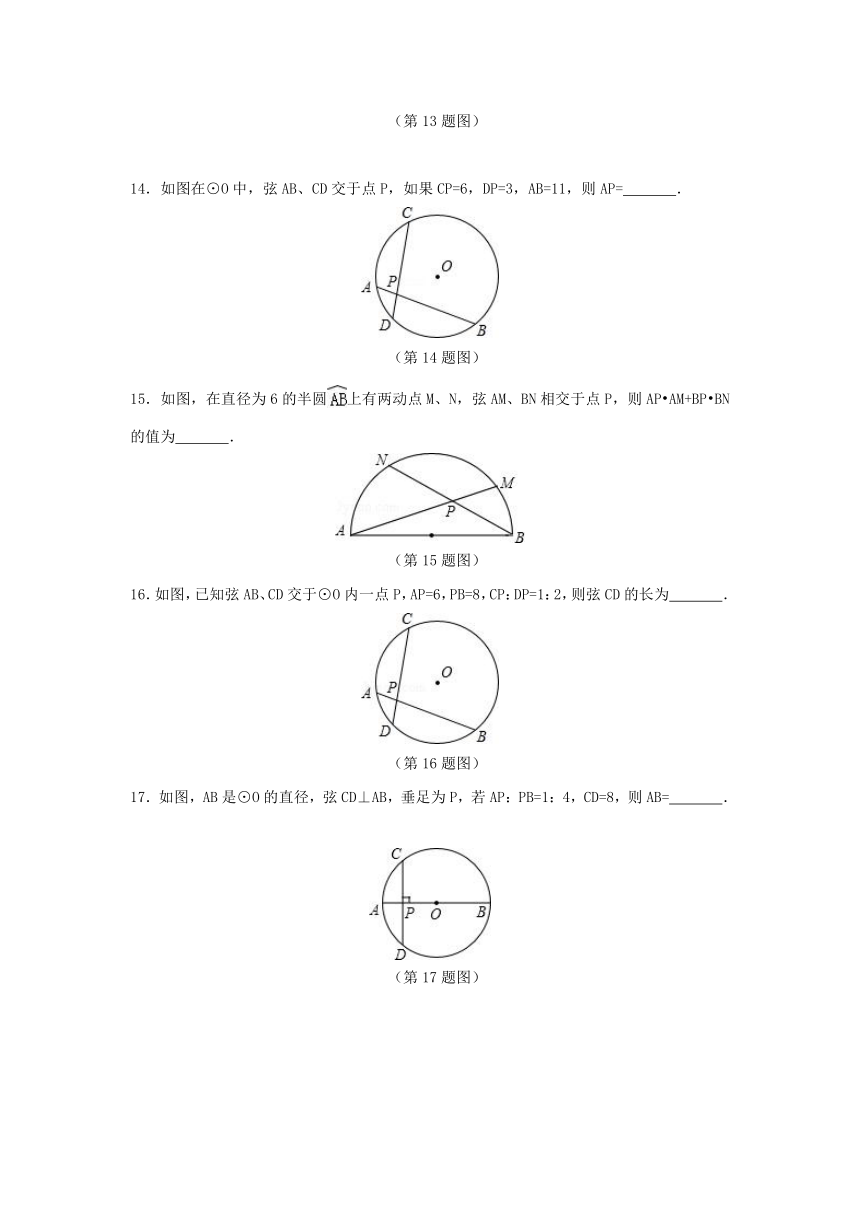
9.在半径为R的圆内,长为R的弦所对的圆周角为( )
A.30°或150° B.60°或120° C.60° D.30°
10.如图,AB是半圆的直径,O为圆心,C是半圆上的点,D是上的点,若∠BOC=40°,则∠D的度数为( )
(第10题图)
A.100° B.110° C.120° D.130°
二.填空题(共7小题)
11.如图,⊙O的弦AB、CD相交于点P,已知CP=3,PD=4,AP=2,那么AB= .
(第11题图)
12.如图,⊙O中弦AB,CD相交于点P,已知AP=3,BP=2,CP=1,则DP= .
(第12题图)
13.如图,点P为弦AB上的一点,连接OP,过点P作PC⊥OP,PC交⊙O于点C,若AP=9,BP=4,则PC= .
(第13题图)
14.如图在⊙O中,弦AB、CD交于点P,如果CP=6,DP=3,AB=11,则AP= .
(第14题图)
15.如图,在直径为6的半圆上有两动点M、N,弦AM、BN相交于点P,则AP?AM+BP?BN的值为 .
(第15题图)
16.如图,已知弦AB、CD交于⊙O内一点P,AP=6,PB=8,CP:DP=1:2,则弦CD的长为 .
(第16题图)
17.如图,AB是⊙O的直径,弦CD⊥AB,垂足为P,若AP:PB=1:4,CD=8,则AB= .
(第17题图)
三.解答题(共4小题)
18.如图,AB、CD是⊙O的直径,弦CE∥AB,的度数为70°.求∠EOC的度数.
(第18题图)
19.已知△ABC,以AB为直径的⊙O分别交AC于点D,BC于点E,连接ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=2,求CD的长.
(第19题图)
20.如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.
(第20题图)
21.已知:如图1,在⊙O中,直径AB=4,CD=2,直线AD,BC相交于点E.
(1)∠E的度数为 ;
(2)如图2,AB与CD交于点F,请补全图形并求出∠E的度数;
(3)如图3,弦AB与弦CD不相交,求∠AEC的度数.
(第21题图)
参考答案
一.1.D【解析】在圆上取一点A,连接AB,AD.∵点A、B,C,D在⊙O上,∠BCD=130°,∴∠BAD=50°,∴∠BOD=100°.故选D.
(第1题答图)
【点评】此题考查了圆周角的性质与圆的内接四边形的性质.此题比较简单,解题的关键是注意数形结合思想的应用,注意辅助线的作法.
2.A【解析】∵A、B、C是⊙O上的三点,∠A+∠C=75°,∴∠B=75°,∴∠AOC=2∠B=150°.故选A.
【点评】本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.
3.C【解析】∵∠AOD=130°,∴∠C=90°﹣.故选C.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.
4.C【解析】∵AB为⊙O的直径,∴∠ACB=90°.∵∠CBA=25°,∴∠CAB=90°﹣∠CBA=65°,∴∠D=∠CAB=65°.故选C.
【点评】此题考查了圆周角定理.此题难度不大,注意掌握直径所对的圆周角等于直角与在同圆或等圆中,同弧或等弧所对的圆周角相等定理的应用是解此题的关键.
5.B【解析】∵∠AOB=80°,∴∠ACB=∠AOB=40°.故选B.
【点评】本题考查了圆周角定理:一条弧所对的圆周角是它所对的圆心角的一半.
6.D 【解析】连接OC,∵点C把半圆三等分,∴∠AOC=120°,∴∠D=60°或90°﹣60°=30°.故选D.
(第6题答图)
【点评】此题考查圆周角定理,关键是根据圆周角定理解答.
7.A【解析】∵∠AOC=2∠B,∠AOC=100°,∴∠B=50°.∵OM∥BC,∴∠AMO=∠B=50°,
故选A.
【点评】本题考查了圆周角定理,熟练掌握圆周角定理,并找到∠AMO与∠B的关系,已知角与∠B的关系,从而求出角的度数.
8.B【解析】∵AC是⊙O的直径,∴∠ABC=90°.∵∠ACB=52°,∴∠A=90°﹣∠ACB=38°,
∴∠D=∠A=38°.故选B.
【点评】此题考查了圆周角定理与直角三角形的性质.此题比较简单,注意掌握直径所对的圆周角是直角与在同圆或等圆中,同弧或等弧所对的圆周角相等定理的应用是解此题的关键.
9.A【解析∵半径为R,长度为R的弦,∴这条弦和两条半径组成了一个等边三角形,∴该弦所对的圆心角是60°,①当圆周角的顶点在优弧上时,得此圆周角等于30°;②当圆周角的顶点在劣弧上,得此圆周角等于150°.故选A.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半,注意:此类题一定要分情况考虑.即一条弦所对的圆周角有两种情况,且两种情况中的角是互补的关系.
10.B【解析】∵∠BOC=40°,∴∠AOC=180°﹣40°=140°,∴∠D=.故选B.
【点评】此题考查圆周角定理,关键是根据互补得出∠AOC的度数.
二.11.8【解析】由相交弦定理,得PA?PB=PC?PD,∴BP===6,
∴AB=8.
【点评】本题主要考查相交弦定理:圆内两弦相交于圆内一点,各弦被这点所分得的两线段的长的乘积相等.
12.6【解析】由相交弦定理,得AP?BP=CP?DP,则DP==6,
【点评】本题考查的是相交弦定理的应用,相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等.
13.6【解析】延长CP交⊙O于点D.∵PC⊥OP,∴PC=PD.∵PC?PD=PA?PB,∴PC2=PA?PB.
∵AP=9,BP=4,∴PC2=4×9.解得PC=6.
(第13题答图)
【点评】本题考查了相交弦定理与垂径定理.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.
14.2或9【解析】根据相交弦定理,得AP?PB=CP?DP.∵AB=11,∴AP(11﹣AP)=CP?DP,∴AP2﹣11AP+18=0,∴AP=2或9.
【点评】此题主要是运用了相交弦定理.
15.36【解析】连接AN、BM.∵AB是直径,∴∠AMB=90°,∴BP2=MP2+BM2 .∵AP?PM=BP?PN,
原式=AP(AP+PM)+BP(BP+PN)=AP2+AP?PM+BP2+BP?PN
=AP2+BP2+2AP?PM
=AP2+MP2+BM2+2AP?PM
=BM2+(AP+PM)2=BM2+AM2=AB2=36.
(第15题答图)
【点评】本题利用了圆周角定理和相交弦定理,勾股定理求解.
16.6【解析】∵CP:DP=1:2,∴DP=2CP.∵PA?PB=PC?PD,∴6×8=PC×2PC.解得PC=2(舍去负值)∴CD=PC+PD=3PC=6.
【点评】本题主要考查相交弦定理“圆内两弦相交于圆内一点,各弦被这点所分得的两线段的长的乘积相等”的应用.
17.10【解析】∵AB是⊙O的直径,弦CD⊥AB,CD=8,∴CP=4.根据相交弦定理,得16=AP×4AP,解得AP=2,∴AB=10.
【点评】本题主要考查了垂径定理及相交弦定理.
三、18.解:连接OE.
∵的度数为70°,
∴∠AOC=70°.
∵CE∥AB,
∴∠C=∠AOC=70°.
∵OC=OE,
∴∠C=∠E=70°,
∴∠EOC=180°﹣70°﹣70°=40°.
(第18题答图)
【点评】本题考查的是圆周角定理,掌握平行线的性质、等腰三角形的性质以及三角形内角和定理是解题的关键.
19.(1)证明:∵ED=EC,
∴∠EDC=∠C.
∵∠EDC=∠B,(∠EDC+∠ADE=180°,∠B+∠ADE=180°,∴∠EDC=∠B)
∴∠B=∠C,
∴AB=AC.
(2)方法一:
解:连接AE.
∵AB为直径,
∴AE⊥BC.
由(1)知,AB=AC,
∴BE=CE=BC=.
∵△CDE∽△CBA,
∴,
∴CE?CB=CD?CA,AC=AB=4,
∴?2=4CD,
∴CD=.
方法二:
解:连接BD,
∵AB为直径,
∴BD⊥AC,
设CD=a.
由(1)知AC=AB=4,
则AD=4﹣a.
在Rt△ABD中,由勾股定理,可得
BD2=AB2﹣AD2=42﹣(4﹣a)2
在Rt△CBD中,由勾股定理,可得
BD2=BC2﹣CD2=(2)2﹣a2
∴42﹣(4﹣a)2=(2)2﹣a2
整理,得a=,
即CD=.
(第19题答图)
【点评】本题考查了圆周角定理,等腰三角形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.
20.解:(1)∵AB是半圆O的直径,
∴∠ACB=90°.
又∵OD∥BC,
∴∠AEO=90°,即OE⊥AC,∠CAB=90°﹣∠B=90°﹣70°=20°,∠AOD=∠B=70°.
∵OA=OD,
∴∠DAO=∠ADO===55°,
∴∠CAD=∠DAO﹣∠CAB=55°﹣20°=35°;
(2)在直角△ABC中,BC===.
∵OE⊥AC,
∴AE=EC.
又∵OA=OB,
∴OE=BC=.
又∵OD=AB=2,
∴DE=OD﹣OE=2﹣.
21.解:(1)如图1,连结OD,OC,BD.
∵OD=OC=CD=2,
∴△DOC为等边三角形,
∴∠DOC=60°,
∴∠DBC=30°,
∴∠EBD=30°.
∵AB为直径,
∴∠ADB=90°,
∴∠E=90°﹣300=600,
∠E的度数为600;
(2)①如图2,直线AD,CB交于点E,连结OD,OC,AC.
∵OD=OC=CD=2,
∴△DOC为等边三角形,
∴∠DOC=60°,
∴∠DAC=30°,
∴∠EBD=30°.
∵AB为直径,
∴∠ACB=90°,
∴∠E=90°﹣30°=60°,
(3)如图3,连结OD,OC,
(第21题答图)
∵OD=OC=CD=2,
∴△DOC为等边三角形,
∴∠DOC=60°,
∴∠CBD=30°,
∴∠ADB=90°,
∴∠BED=60°,
∴∠AEC=60°.
【点评】本题考查的是圆周角定理及其推论、等边三角形的性质,解题的关键是正确作出辅助线,构造直角三角形,利用直径所对的圆周角是直角进行解答.
一.选择题(共10小题)
1.如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是( )
(第1题图)
A.50° B.60° C.80° D.100°
2.如图,A、B、C是⊙O上的三点,若∠A+∠C=75°,则∠AOC的度数为( )
(第2题图)
A.150° B.140° C.130° D.120°
3.如图,AB是⊙O的直线,C是⊙O上一点(A、B除外),∠AOD=130°,则∠C的度数是( )
(第3题图)
A.50° B.60° C.25° D.30°
4.如图,已知AB是⊙O的直径,∠CBA=25°,则∠D的度数为( )
(第4题图)
A.25° B.50° C.65° D.75°
5.如图,点A、B、C是⊙O上的点,∠AOB=80°,则∠ACB的度数是( )
(第5题图)
A.30° B.40° C.45° D.80°
6.如图,AB是⊙O的直径,C、D为⊙O上位于AB异侧的两个点,当点C把半圆三等分时,∠D的度数为( )
(第6题图)
A.30° B.45° C.60° D.30°或60°
7.如图,AB、BC是⊙O的弦,OM∥BC交AB于点M,若∠AOC=100°,则∠AMO的度数为( )
(第7题图)
A.50° B.35° C.25° D.20°
8.如图,△ABC⊙O,⊙O,AC是⊙O的直径,∠ACB=52°,D是上一点,则∠D的度数是( )
(第8题图)
A.52° B.38° C.19° D.26°
9.在半径为R的圆内,长为R的弦所对的圆周角为( )
A.30°或150° B.60°或120° C.60° D.30°
10.如图,AB是半圆的直径,O为圆心,C是半圆上的点,D是上的点,若∠BOC=40°,则∠D的度数为( )
(第10题图)
A.100° B.110° C.120° D.130°
二.填空题(共7小题)
11.如图,⊙O的弦AB、CD相交于点P,已知CP=3,PD=4,AP=2,那么AB= .
(第11题图)
12.如图,⊙O中弦AB,CD相交于点P,已知AP=3,BP=2,CP=1,则DP= .
(第12题图)
13.如图,点P为弦AB上的一点,连接OP,过点P作PC⊥OP,PC交⊙O于点C,若AP=9,BP=4,则PC= .
(第13题图)
14.如图在⊙O中,弦AB、CD交于点P,如果CP=6,DP=3,AB=11,则AP= .
(第14题图)
15.如图,在直径为6的半圆上有两动点M、N,弦AM、BN相交于点P,则AP?AM+BP?BN的值为 .
(第15题图)
16.如图,已知弦AB、CD交于⊙O内一点P,AP=6,PB=8,CP:DP=1:2,则弦CD的长为 .
(第16题图)
17.如图,AB是⊙O的直径,弦CD⊥AB,垂足为P,若AP:PB=1:4,CD=8,则AB= .
(第17题图)
三.解答题(共4小题)
18.如图,AB、CD是⊙O的直径,弦CE∥AB,的度数为70°.求∠EOC的度数.
(第18题图)
19.已知△ABC,以AB为直径的⊙O分别交AC于点D,BC于点E,连接ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=2,求CD的长.
(第19题图)
20.如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.
(第20题图)
21.已知:如图1,在⊙O中,直径AB=4,CD=2,直线AD,BC相交于点E.
(1)∠E的度数为 ;
(2)如图2,AB与CD交于点F,请补全图形并求出∠E的度数;
(3)如图3,弦AB与弦CD不相交,求∠AEC的度数.
(第21题图)
参考答案
一.1.D【解析】在圆上取一点A,连接AB,AD.∵点A、B,C,D在⊙O上,∠BCD=130°,∴∠BAD=50°,∴∠BOD=100°.故选D.
(第1题答图)
【点评】此题考查了圆周角的性质与圆的内接四边形的性质.此题比较简单,解题的关键是注意数形结合思想的应用,注意辅助线的作法.
2.A【解析】∵A、B、C是⊙O上的三点,∠A+∠C=75°,∴∠B=75°,∴∠AOC=2∠B=150°.故选A.
【点评】本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.
3.C【解析】∵∠AOD=130°,∴∠C=90°﹣.故选C.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.
4.C【解析】∵AB为⊙O的直径,∴∠ACB=90°.∵∠CBA=25°,∴∠CAB=90°﹣∠CBA=65°,∴∠D=∠CAB=65°.故选C.
【点评】此题考查了圆周角定理.此题难度不大,注意掌握直径所对的圆周角等于直角与在同圆或等圆中,同弧或等弧所对的圆周角相等定理的应用是解此题的关键.
5.B【解析】∵∠AOB=80°,∴∠ACB=∠AOB=40°.故选B.
【点评】本题考查了圆周角定理:一条弧所对的圆周角是它所对的圆心角的一半.
6.D 【解析】连接OC,∵点C把半圆三等分,∴∠AOC=120°,∴∠D=60°或90°﹣60°=30°.故选D.
(第6题答图)
【点评】此题考查圆周角定理,关键是根据圆周角定理解答.
7.A【解析】∵∠AOC=2∠B,∠AOC=100°,∴∠B=50°.∵OM∥BC,∴∠AMO=∠B=50°,
故选A.
【点评】本题考查了圆周角定理,熟练掌握圆周角定理,并找到∠AMO与∠B的关系,已知角与∠B的关系,从而求出角的度数.
8.B【解析】∵AC是⊙O的直径,∴∠ABC=90°.∵∠ACB=52°,∴∠A=90°﹣∠ACB=38°,
∴∠D=∠A=38°.故选B.
【点评】此题考查了圆周角定理与直角三角形的性质.此题比较简单,注意掌握直径所对的圆周角是直角与在同圆或等圆中,同弧或等弧所对的圆周角相等定理的应用是解此题的关键.
9.A【解析∵半径为R,长度为R的弦,∴这条弦和两条半径组成了一个等边三角形,∴该弦所对的圆心角是60°,①当圆周角的顶点在优弧上时,得此圆周角等于30°;②当圆周角的顶点在劣弧上,得此圆周角等于150°.故选A.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半,注意:此类题一定要分情况考虑.即一条弦所对的圆周角有两种情况,且两种情况中的角是互补的关系.
10.B【解析】∵∠BOC=40°,∴∠AOC=180°﹣40°=140°,∴∠D=.故选B.
【点评】此题考查圆周角定理,关键是根据互补得出∠AOC的度数.
二.11.8【解析】由相交弦定理,得PA?PB=PC?PD,∴BP===6,
∴AB=8.
【点评】本题主要考查相交弦定理:圆内两弦相交于圆内一点,各弦被这点所分得的两线段的长的乘积相等.
12.6【解析】由相交弦定理,得AP?BP=CP?DP,则DP==6,
【点评】本题考查的是相交弦定理的应用,相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等.
13.6【解析】延长CP交⊙O于点D.∵PC⊥OP,∴PC=PD.∵PC?PD=PA?PB,∴PC2=PA?PB.
∵AP=9,BP=4,∴PC2=4×9.解得PC=6.
(第13题答图)
【点评】本题考查了相交弦定理与垂径定理.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.
14.2或9【解析】根据相交弦定理,得AP?PB=CP?DP.∵AB=11,∴AP(11﹣AP)=CP?DP,∴AP2﹣11AP+18=0,∴AP=2或9.
【点评】此题主要是运用了相交弦定理.
15.36【解析】连接AN、BM.∵AB是直径,∴∠AMB=90°,∴BP2=MP2+BM2 .∵AP?PM=BP?PN,
原式=AP(AP+PM)+BP(BP+PN)=AP2+AP?PM+BP2+BP?PN
=AP2+BP2+2AP?PM
=AP2+MP2+BM2+2AP?PM
=BM2+(AP+PM)2=BM2+AM2=AB2=36.
(第15题答图)
【点评】本题利用了圆周角定理和相交弦定理,勾股定理求解.
16.6【解析】∵CP:DP=1:2,∴DP=2CP.∵PA?PB=PC?PD,∴6×8=PC×2PC.解得PC=2(舍去负值)∴CD=PC+PD=3PC=6.
【点评】本题主要考查相交弦定理“圆内两弦相交于圆内一点,各弦被这点所分得的两线段的长的乘积相等”的应用.
17.10【解析】∵AB是⊙O的直径,弦CD⊥AB,CD=8,∴CP=4.根据相交弦定理,得16=AP×4AP,解得AP=2,∴AB=10.
【点评】本题主要考查了垂径定理及相交弦定理.
三、18.解:连接OE.
∵的度数为70°,
∴∠AOC=70°.
∵CE∥AB,
∴∠C=∠AOC=70°.
∵OC=OE,
∴∠C=∠E=70°,
∴∠EOC=180°﹣70°﹣70°=40°.
(第18题答图)
【点评】本题考查的是圆周角定理,掌握平行线的性质、等腰三角形的性质以及三角形内角和定理是解题的关键.
19.(1)证明:∵ED=EC,
∴∠EDC=∠C.
∵∠EDC=∠B,(∠EDC+∠ADE=180°,∠B+∠ADE=180°,∴∠EDC=∠B)
∴∠B=∠C,
∴AB=AC.
(2)方法一:
解:连接AE.
∵AB为直径,
∴AE⊥BC.
由(1)知,AB=AC,
∴BE=CE=BC=.
∵△CDE∽△CBA,
∴,
∴CE?CB=CD?CA,AC=AB=4,
∴?2=4CD,
∴CD=.
方法二:
解:连接BD,
∵AB为直径,
∴BD⊥AC,
设CD=a.
由(1)知AC=AB=4,
则AD=4﹣a.
在Rt△ABD中,由勾股定理,可得
BD2=AB2﹣AD2=42﹣(4﹣a)2
在Rt△CBD中,由勾股定理,可得
BD2=BC2﹣CD2=(2)2﹣a2
∴42﹣(4﹣a)2=(2)2﹣a2
整理,得a=,
即CD=.
(第19题答图)
【点评】本题考查了圆周角定理,等腰三角形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.
20.解:(1)∵AB是半圆O的直径,
∴∠ACB=90°.
又∵OD∥BC,
∴∠AEO=90°,即OE⊥AC,∠CAB=90°﹣∠B=90°﹣70°=20°,∠AOD=∠B=70°.
∵OA=OD,
∴∠DAO=∠ADO===55°,
∴∠CAD=∠DAO﹣∠CAB=55°﹣20°=35°;
(2)在直角△ABC中,BC===.
∵OE⊥AC,
∴AE=EC.
又∵OA=OB,
∴OE=BC=.
又∵OD=AB=2,
∴DE=OD﹣OE=2﹣.
21.解:(1)如图1,连结OD,OC,BD.
∵OD=OC=CD=2,
∴△DOC为等边三角形,
∴∠DOC=60°,
∴∠DBC=30°,
∴∠EBD=30°.
∵AB为直径,
∴∠ADB=90°,
∴∠E=90°﹣300=600,
∠E的度数为600;
(2)①如图2,直线AD,CB交于点E,连结OD,OC,AC.
∵OD=OC=CD=2,
∴△DOC为等边三角形,
∴∠DOC=60°,
∴∠DAC=30°,
∴∠EBD=30°.
∵AB为直径,
∴∠ACB=90°,
∴∠E=90°﹣30°=60°,
(3)如图3,连结OD,OC,
(第21题答图)
∵OD=OC=CD=2,
∴△DOC为等边三角形,
∴∠DOC=60°,
∴∠CBD=30°,
∴∠ADB=90°,
∴∠BED=60°,
∴∠AEC=60°.
【点评】本题考查的是圆周角定理及其推论、等边三角形的性质,解题的关键是正确作出辅助线,构造直角三角形,利用直径所对的圆周角是直角进行解答.
