新版沪科版2019-2020学年九年级数学下册24.4直线与圆的位置关系作业设计(含答案)
文档属性
| 名称 | 新版沪科版2019-2020学年九年级数学下册24.4直线与圆的位置关系作业设计(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 364.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-03 21:52:22 | ||
图片预览


文档简介
24.4 直线与圆的位置关系
一.选择题(共8小题)
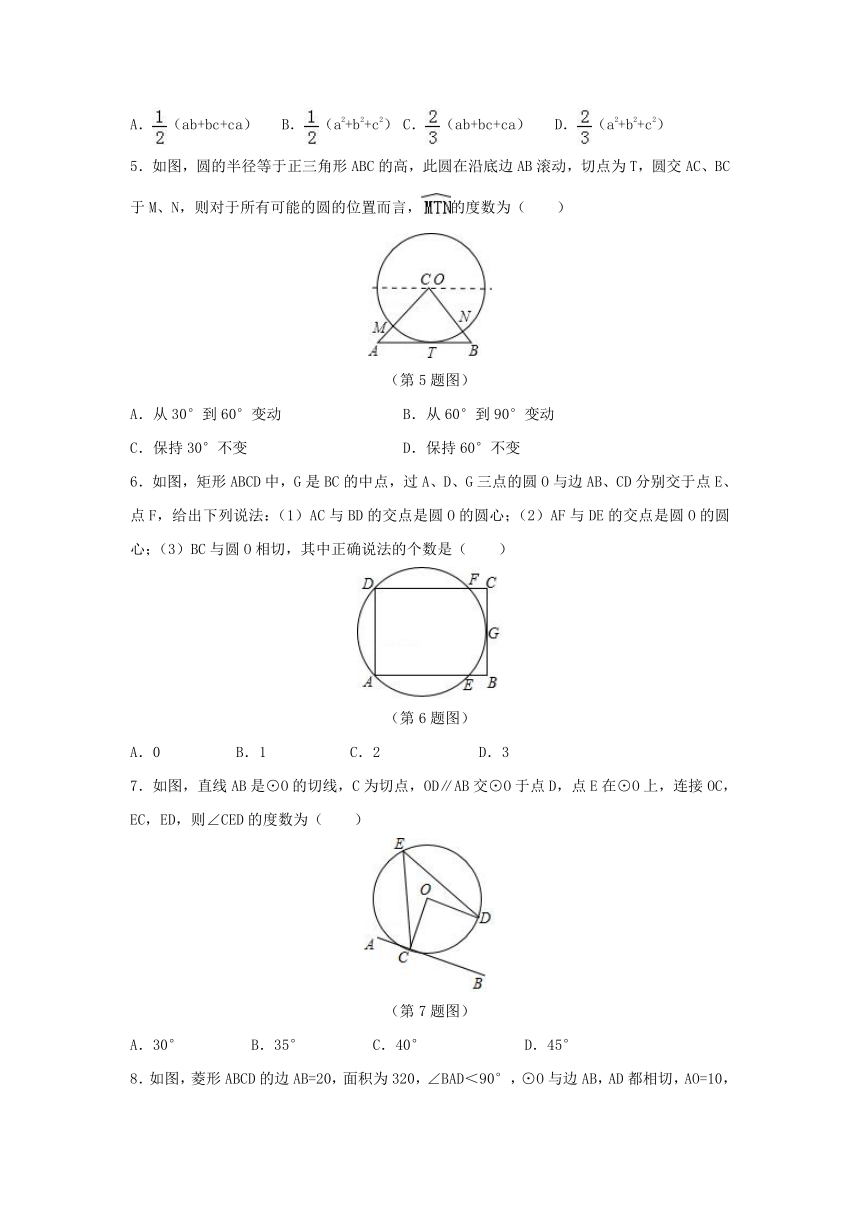
1.如图,△ABC是一张三角形的纸片,⊙O是它的内切圆,D是其中的一个切点,已知AD=10cm,小明准备用剪刀沿着与⊙O相切的任意一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长为( )
(第1题图)
A.20cm B.15cm
C.10cm D.随直线MN的变化而变化
2.以半圆中的一条弦BC(非直径)为对称轴将弧BC折叠后与直径AB交于点D,若,且AB=10,则CB的长为( )
(第2题图)
A. B. C. D.4
3.以正方形ABCD的BC边为直径作半圆O,过点D作直线切半圆于点F,交AB边于点E.则三角形ADE和直角梯形EBCD的周长之比为( )
(第3题图)
A.3:4 B.4:5 C.5:6 D.6:7
4.设H为锐角△ABC的三条高AD、BE、CF的交点,若BC=a,AC=b,AB=c,则AH?AD+BH?BE+CH?CF等于( )
A.(ab+bc+ca) B.(a2+b2+c2) C.(ab+bc+ca) D.(a2+b2+c2)
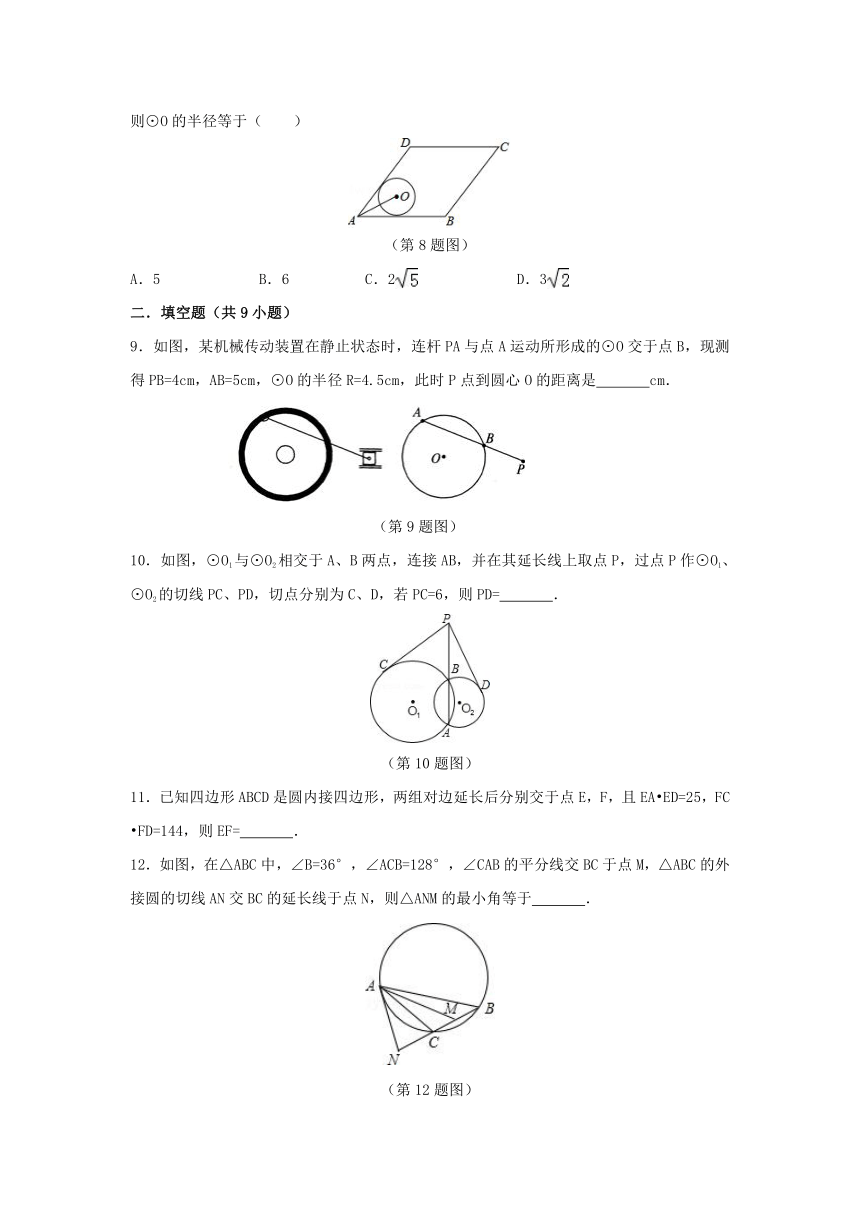
5.如图,圆的半径等于正三角形ABC的高,此圆在沿底边AB滚动,切点为T,圆交AC、BC于M、N,则对于所有可能的圆的位置而言,的度数为( )
(第5题图)
A.从30°到60°变动 B.从60°到90°变动
C.保持30°不变 D.保持60°不变
6.如图,矩形ABCD中,G是BC的中点,过A、D、G三点的圆O与边AB、CD分别交于点E、点F,给出下列说法:(1)AC与BD的交点是圆O的圆心;(2)AF与DE的交点是圆O的圆心;(3)BC与圆O相切,其中正确说法的个数是( )
(第6题图)
A.0 B.1 C.2 D.3
7.如图,直线AB是⊙O的切线,C为切点,OD∥AB交⊙O于点D,点E在⊙O上,连接OC,EC,ED,则∠CED的度数为( )
(第7题图)
A.30° B.35° C.40° D.45°
8.如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径等于( )
(第8题图)
A.5 B.6 C.2 D.3
二.填空题(共9小题)
9.如图,某机械传动装置在静止状态时,连杆PA与点A运动所形成的⊙O交于点B,现测得PB=4cm,AB=5cm,⊙O的半径R=4.5cm,此时P点到圆心O的距离是 cm.
(第9题图)
10.如图,⊙O1与⊙O2相交于A、B两点,连接AB,并在其延长线上取点P,过点P作⊙O1、⊙O2的切线PC、PD,切点分别为C、D,若PC=6,则PD= .
(第10题图)
11.已知四边形ABCD是圆内接四边形,两组对边延长后分别交于点E,F,且EA?ED=25,FC?FD=144,则EF= .
12.如图,在△ABC中,∠B=36°,∠ACB=128°,∠CAB的平分线交BC于点M,△ABC的外接圆的切线AN交BC的延长线于点N,则△ANM的最小角等于 .
(第12题图)
13.如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,BP的长为 .
(第13题图)
14.如图,在矩形ABCD中,AB=5,BC=4,以CD为直径作⊙O.将矩形ABCD绕点C旋转,
使所得矩形A′B′CD′的边A′B′与⊙O相切,切点为E,边CD′与⊙O相交于点F,
则CF的长为 .
(第14题图)
15.如图,AT切⊙O于点A,AB是⊙O的直径.若∠ABT=40°,则∠ATB= .
(第15题图)
16.如图,已知∠AOB=30°,在射线OA上取点O1,以O1为圆心的圆与OB相切;在射线O1A上取点O2,以O2为圆心,O2O1为半径的圆与OB相切;在射线O2A上取点O3,以O3为圆心,O3O2为半径的圆与OB相切;…;在射线O9A上取点O10,以O10为圆心,O10O9为半径的圆与OB相切.若⊙O1的半径为1,则⊙O10的半径长是 .
(第16题图)
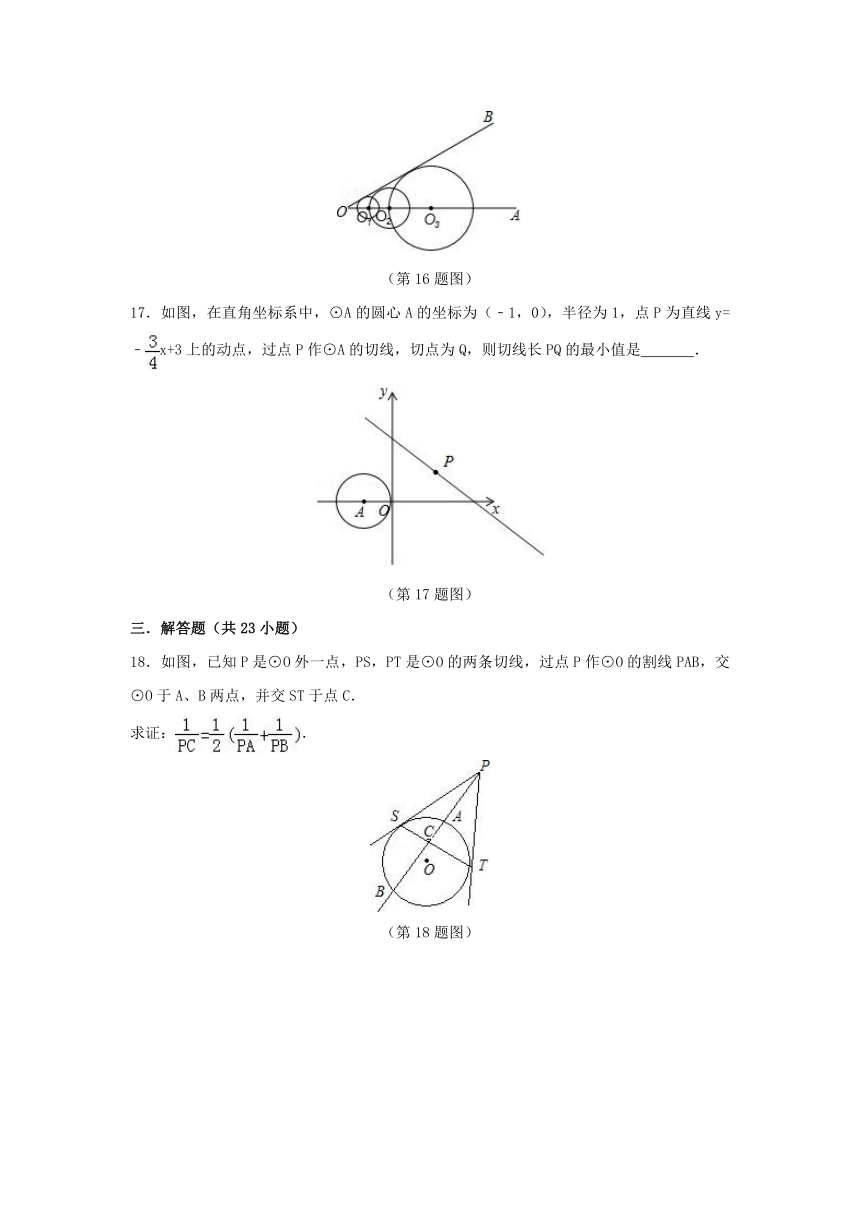
17.如图,在直角坐标系中,⊙A的圆心A的坐标为(﹣1,0),半径为1,点P为直线y=﹣x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是 .
(第17题图)
三.解答题(共23小题)
18.如图,已知P是⊙O外一点,PS,PT是⊙O的两条切线,过点P作⊙O的割线PAB,交⊙O于A、B两点,并交ST于点C.
求证:.
(第18题图)
19.如图,Rt△BDE中,∠BDE=90°,BC平分∠DBE交DE于点C,AC⊥CB交BE于点A,△ABC的外接圆的半径为r.
(1)若∠E=30°,求证:BC?BD=r?ED;
(2)若BD=3,DE=4,求AE的长.
(第19题图)
20.如图,两个同心圆的圆心是O,大圆的半径为13,小圆的半径为5,AD是大圆的直径.大圆的弦AB,BE分别与小圆相切于点C,F.AD,BE相交于点G,连接BD.
(1)求BD的长;
(2)求∠ABE+2∠D的度数;
(3)求的值.
(第20题图)
21.如图,△ABC内接于⊙O,过点B作⊙O的切线,交于CA的延长线于点E,∠EBC=2∠C.
(1)求证:AB=AC;
(2)当=时,①求tan∠ABE的值;②如果AE=,求AC的值.
(第21题图)
22.如图,⊙Ol和⊙O2内切于点P,过点P的直线交⊙Ol于点D,交⊙O2于点E,DA与⊙O2相切,切点为C.
(1)求证:PC平分∠APD;
(2)求证:PD?PA=PC2+AC?DC;
(3)若PE=3,PA=6,求PC的长.
(第22题图)
参考答案
一.1.A【解析】∵△ABC是一张三角形的纸片,⊙O是它的内切圆,D是其中的一个切点,AD=10cm,∴设E、F分别是⊙O的切点,故DM=MF,FN=EN,AD=AE,∴AM+AN+MN=AD+AE=10+10=20(cm).故选A.
(第1题答图)
【点评】此题主要考查了切线长定理,得出AM+AN+MN=AD+AE是解题的关键.
2.A【解析】如图,若,且AB=10,∴AD=4,BD=6,作AB关于直线BC的对称线段A′B,交半圆于D′,连接AC、CA′,可得A、C、A′三点共线.∵线段A′B与线段AB关于直线BC对称,∴AB=A′B,∴AC=A′C,AD=A′D′=4,A′B=AB=10.而A′C?A′A=A′D′?A′B,即A′C?2A′C=4×10=40.则A′C2=20.又∵A′C2=A′B2﹣CB2,∴20=100﹣CB2,∴CB=4.
故选A.
(第2题图)
【点评】此题将翻折变换、勾股定理、割线定理相结合,考查了同学们的综合应用能力,要善于观察图形的特点,然后做出解答.
3.D【解析】根据切线长定理,得BE=EF,DF=DC=AD=AB=BC.设EF=x,DF=y,则在直角△AED中,AE=y﹣x,AD=CD=y,DE=x+y.根据勾股定理,可得(y﹣x)2+y2=(x+y)2,∴y=4x,∴三角形ADE的周长为12x,直角梯形EBCD的周长为14x,∴两者周长之比为12x:14x=6:7.
故选D.
【点评】此题考查圆的切线长定理,正方形的性质和勾股定理等知识,解答本题关键是运用切线长定理得出EB=EF,DF=DC,从而求解.
4.B【解析】AH?AD=AC?AE=AC?AB?cos∠BAE=(b2+c2﹣a2),同理BH?BE=(a2+c2﹣b2),CH?CF=(a2+b2﹣c2),故AH?AD+BH?BE+CH?CF=(a2+b2+c2).故选B.
【点评】本题主要考查了切割线定理,理解H、D、C、E四点共圆是解决本题的关键.
5.D【解析】过点O作OH∥AC,交AB与点H,交BC于点Z,过点O作OE∥BC,交AB的延长线于点E,连接OM,ON,过点M作MG⊥OH于点G,作NK⊥OE于点K.∵△ACB是等边三角形,∴∠A=∠ACB=∠ABC=60°.∵OE∥BC,∴∠ACB=∠CZO=60°.∴∠HZB=60°.∵OE∥CB,∴∠EOH=∠HZB=60°.∵OC∥AB,∴四边形AHOC是平行四边形,∴∠A=∠COZ=60°,∴△OZC是等边三角形.∵MG⊥OH,NK⊥OH,∴MG,NK均为△OZC的高,∴MG=NK.在Rt△OMG与Rt△ONK中,∵,∴△OMG≌△ONK(HL),∴∠MOG=∠KON,∴∠MON=60°,∴的度数为60°.故选D.
(第5题答图)
【点评】本题考查的是切线的性质,根据题意作出辅助线,构造出平行四边形及等边三角形,利用圆心角与弧的关系求解是解答此题的关键.
6.C【解析】连接DG、AG,作GH⊥AD于点H,连接OD,如图.∵G是BC的中点,∴AG=DG,∴GH垂直平分AD,∴点O在HG上.∵AD∥BC,∴HG⊥BC,∴BC与圆O相切.∵OG=OD,∴点O不是HG的中点,∴圆心O不是AC与BD的交点.而四边形AEFD为⊙O的内接矩形,∴AF与DE的交点是圆O的圆心;∴(1)错误,(2)(3)正确.故选C.
(第6题答图)
【点评】本题考查了三角形内切圆与内心:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.也考查了矩形的性质.
7.D【解析】∵直线AB是⊙O的切线,C为切点,∴∠OCB=90°.∵OD∥AB,∴∠COD=90°,
∴∠CED=∠COD=45°.故选D.
【点评】本题主要考查切线的性质,解题的关键是掌握圆的切线垂直于经过切点的半径及圆周角定理.
8.C【解析】如图作DH⊥AB于点H,连接BD,延长AO交BD于点E.
(第8题答图)
∵菱形ABCD的边AB=20,面积为320,∴AB?DH=320,∴DH=16.在Rt△ADH中,AH==12,∴HB=AB﹣AH=8.在Rt△BDH中,BD==8.设⊙O与AB相切于F,连接OF.∵AD=AB,OA平分∠DAB,∴AE⊥BD.∵∠OAF+∠ABE=90°,∠ABE+∠BDH=90°,
∴∠OAF=∠BDH,∵∠AFO=∠DHB=90°,∴△AOF∽△DBH,∴=,∴=,
∴OF=2.故选C.
【点评】本题考查切线的性质、菱形的性质、勾股定理、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.
二.9.7.5【解析】连接PO交圆于点C,并延长PO交圆于点D.∵PB=4cm,AB=5cm,∴PA=9cm;
由割线定理,得PB?PA=PC?PD;设点P到圆心的距离是xcm,则有(x﹣4.5)(x+4.5)=36,
解得x=7.5cm.故P到O点的距离为7.5cm.
(第9题答图)
【点评】此题要通过作辅助线构造割线,然后运用割线定理列方程求解.
10.6【解析】∵依题意,可得PC2=PB?PA,PD2=PA?PB,∴PC2=PD2.∵PC=6,∴PC=PD=6.
【点评】注意:切割线定理和割线定理必须在同一个圆中运用;这里借助割线PBA建立了两条切线长的相等关系.
11.13【解析】∵∠A=∠BCF=∠CFE+∠CE∴在∠A内作∠EAG交EF于点G,使∠EAG=∠DFE,则∠FAG=∠FEB.在△EAG和△EFD中,∠EAG=∠DFE,∠AEG=∠FED,则△EAG∽△EFD,∴EA:EF=EG:ED,即EG×EF=EA×ED(1).在△EFB和△AFG中,∠FAG=∠FEB,∠AFG=∠EFB,
所以△EFB∽△AFG,∴AF:EF=FG:FB,即FG×EF=AF×BF (2),(1)+(2),得EG×EF+FG×EF=EA×ED+AF×BF,EF×(EG+FG)=EA×ED+AF×BF,即EF2=EA×ED+AF×BF,由割线定理,得到AF×BF=FC×FD,∴EF2=EA×ED+FC×FD=25+144=169,因此EF=13.
(第11题答图)
【点评】本题巧妙地从△EAG∽△EFD和△EFB∽△AFG得到的结论,同切割定理结合起来,从而解得.
12.44°【解析】∵∠B=36°,∠ACB=128°,AM为∠CAB的平分线,∴∠CAM=∠MAB=×(180°﹣36°﹣128°)=8°.∵∠AMC=36°+8°=44°,又AN为切线,∴∠NAC=∠B=36°,∠NAM=44°,∴∠N=180°﹣44°﹣44°=92°,∴△ANM的最小角为44°.
【点评】本题考查了切线的性质、三角形的内角和定理是基础知识比较简单.
13.3或4【解析】如图1中,当⊙P与直线CD相切时,设PC=PM=x.
(第13题答图)
在Rt△PBM中,∵PM2=BM2+PB2,∴x2=42+(8﹣x)2,∴x=5,∴PC=5,BP=BC﹣PC=8﹣5=3.
如图2中当⊙P与直线AD相切时.设切点为K,连接PK,则PK⊥AD,四边形PKDC是矩形.
∴PM=PK=CD=2BM,∴BM=4,PM=8,在Rt△PBM中,PB==4.综上所述,BP的长为3或4.
【点评】本题考查切线的性质、正方形的性质、勾股定理等知识,解题的关键是学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题.
14.4【解析】连接OE,延长EO交CD于点G,作OH⊥B′C于点H,则∠OEB′=∠OHB′=90°.
∵矩形ABCD绕点C旋转所得矩形为A′B′C′D′,∴∠B′=∠B′CD′=90°,AB=CD=5、BC=B′C=4,∴四边形OEB′H和四边形EB′CG都是矩形,OE=OD=OC=2.5,∴B′H=OE=2.5,
∴CH=B′C﹣B′H=1.5,∴CG=B′E=OH===2.∵四边形EB′CG是矩形,∴∠OGC=90°,即OG⊥CD′,∴CF=2CG=4.
(第14题答图)
【点评】本题主要考查圆的切线的判定与性质,解题的关键是掌握矩形的判定与性质、旋转的性质、切线的性质、垂径定理等知识点.
15.50°【解析】∵AT切⊙O于点A,AB是⊙O的直径,∴∠BAT=90°.∵∠ABT=40°,∴∠ATB=50°.
【点评】本题考查切线的性质,解题的关键是根据切线的性质求出∠ATB=90°,本题属于基础题型.
16.29【解析】作O1C、O2D、O3E分别⊥OB.∵∠AOB=30°,∴OO1=2CO1,OO2=2DO2,OO3=2EO3.
∵O1O2=DO2,O2O3=EO3,∴圆的半径呈2倍递增,∴⊙On的半径为2n﹣1 CO1.∵⊙O1的半径为1,
∴⊙O10的半径长=29,
(第16题答图)
【点评】本题考查了圆切线的性质,考查了30°角所对直角边是斜边一半的性质,本题中找出圆半径的规律是解题的关键.
17.2【解析】如图,作AP⊥直线y=﹣x+3,垂足为P,作⊙A的切线PQ,切点为Q,此时切线长PQ最小.∵A的坐标为(﹣1,0),设直线与x轴,y轴分别交于C,B,∴B(0,3),C(4,0),∴OB=3,AC=5,∴BC==5,∴AC=BC,在△APC与△BOC中,,∴△APC≌△BOC,∴AP=OB=3,∴PQ==2.∵PQ2=PA2﹣1,此时PA最小,所以此时切线长PQ也最小,最小值为2.
(第17题答图)
【点评】本题主要考查切线的性质,掌握过切点的半径与切线垂直是解题的关键,用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.
三.18.证明:连PO交ST于点D,则PO⊥ST,连接SO,作OE⊥PB于E,则E为AB中点,
于是.
因为C、E、O、D四点共圆,
所以PC?PE=PD?PO.
又因为Rt△SPD∽Rt△OPS,
所以,
即PS2=PD?PO,
而由切割线定理知,PS2=PA?PB,
所以.
即.
(第18题答图)
【点评】本题主要考查了切割线定理以及三角形相似的证明,注意对比例式的变形是解题关键.
19.(1)证明:取AB中点O,△ABC是Rt△,AB是斜边,O是外接圆心,连接CO,
∴BO=CO,∠BCO=∠OBC.
∵BC是∠DBE平分线,
∴∠DBC=∠CBA,
∴∠OCB=∠DBC,
∴OC∥DB,(内错角相等,两直线平行),
∴,把比例式化为乘积式,得BD?CE=DE?OC.
∵OC=r,
∴BD?CE=DE?r.
∵∠D=90°,∠E=30°,
∴∠DBE=60°,
∴∠CBE=∠DBE=30°,
∴∠CBE=∠E,
∴CE=BC,
∴BC?BD=r?ED.
(2)解:BD=3,DE=4,根据勾股定理,BE=5.
设圆的半径长是r,则OC=OA=r.
∵OC∥DB,
∴△OCE∽△BDE,
∴==,即==,
解得OE=r,CE=r,CH==r.
∵BC平分∠DBE交DE于点C,则△BDC≌△BHC,
∴BH=BD=3,则HE=2.
∴CD=CH=r.
在直角△CHE中,根据勾股定理,得CH2+EH2=CE2,
即(r)2+22=(r)2,解得r=,
则AE=BE﹣2r=5﹣=.
(第19题答图)
【点评】本题考查的是切割线定理,切线的性质定理,勾股定理.
20.解:(1)连接OC,BD.∵AB是小圆的切线,C是切点,
∴OC⊥AB,
∴C是AB的中点.
∵AD是大圆的直径,
∴O是AD的中点.
∴OC是△ABD的中位线.
∴BD=2OC=10.
(2)连接AE.
由(1)知,C是AB的中点.
同理F是BE的中点.
即AB=2BC,BE=2BF,
由切线长定理,得BC=BF.
∴BA=BE.
∴∠BAE=∠E.
∵∠E=∠D,
∴∠ABE+2∠D=∠ABE+∠E+∠BAE=180°.
(3)连接BO.在Rt△OCB中.
∵OB=13,OC=5,
∴BC=12.
由(2)知,∠OBG=∠OBC=∠OAC.
∵∠BGO=∠AGB,
∴△BGO∽△AGB.
∴.
(第20题答图)
【点评】在解本题的过程中要用到切线长定理,中位线定理,相似三角形的判定等知识,要求学生熟练掌握和应用.
21.(1)证明:∵BE切⊙O于点B,
∴∠ABE=∠C.
∵∠EBC=2∠C,即∠ABE+∠ABC=2∠C.
∴∠ABC=∠C.
∴AB=AC.
(2)解:①如图,连接AO,交BC于点F.
∵AB=AC,∴,
∴AO⊥BC,且BF=FC.
∵,∴∴;
设AB=m,BF=2m,
由勾股定理,得AF==;
∴tan∠ABE=tan∠ABF=.
②在△EBA和△ECB中,
∵∠E=∠E,∠EBA=∠ECB,∴△EBA∽△ECB,
∴.
∵,
∴EB=EA.※
由切割线定理,得EB2=EA×EC=EA(EA+AC).
将(※)式代入上式,得EA2=EA(EA+AC);
∵EA≠0,
∴AC=EA=×=4.
(第21题答图)
【点评】本题主要考查了相似三角形的性质,对应边的比相等,以及切割线定理.
22.解:(1)过点P作两圆的公切线PT.
根据弦切角定理,得∠PCD=∠PBC,∠PCB=∠PDC.
∴∠DPC=∠APC,
∴PC平分∠APD;
(2)∵AC?DC=PC?CF,
∴PC2+AC?DC=PC2+PC?CF=PC(PC+CF)=PC?PF.
∵△PDC∽△PFA,
∴PC?PF=PD?PA,
∴PD?PA=PC2+AC?DC;
(3)∵△PCA∽△PEC,
∴=,
即PC2=PA?PE.
∵PE=3,PA=6,
∴PC=3.
(第22题答图)
【点评】本题考查了相似三角形的判定和性质、弦切角定理等知识,综合性强,难度较大.
一.选择题(共8小题)
1.如图,△ABC是一张三角形的纸片,⊙O是它的内切圆,D是其中的一个切点,已知AD=10cm,小明准备用剪刀沿着与⊙O相切的任意一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长为( )
(第1题图)
A.20cm B.15cm
C.10cm D.随直线MN的变化而变化
2.以半圆中的一条弦BC(非直径)为对称轴将弧BC折叠后与直径AB交于点D,若,且AB=10,则CB的长为( )
(第2题图)
A. B. C. D.4
3.以正方形ABCD的BC边为直径作半圆O,过点D作直线切半圆于点F,交AB边于点E.则三角形ADE和直角梯形EBCD的周长之比为( )
(第3题图)
A.3:4 B.4:5 C.5:6 D.6:7
4.设H为锐角△ABC的三条高AD、BE、CF的交点,若BC=a,AC=b,AB=c,则AH?AD+BH?BE+CH?CF等于( )
A.(ab+bc+ca) B.(a2+b2+c2) C.(ab+bc+ca) D.(a2+b2+c2)
5.如图,圆的半径等于正三角形ABC的高,此圆在沿底边AB滚动,切点为T,圆交AC、BC于M、N,则对于所有可能的圆的位置而言,的度数为( )
(第5题图)
A.从30°到60°变动 B.从60°到90°变动
C.保持30°不变 D.保持60°不变
6.如图,矩形ABCD中,G是BC的中点,过A、D、G三点的圆O与边AB、CD分别交于点E、点F,给出下列说法:(1)AC与BD的交点是圆O的圆心;(2)AF与DE的交点是圆O的圆心;(3)BC与圆O相切,其中正确说法的个数是( )
(第6题图)
A.0 B.1 C.2 D.3
7.如图,直线AB是⊙O的切线,C为切点,OD∥AB交⊙O于点D,点E在⊙O上,连接OC,EC,ED,则∠CED的度数为( )
(第7题图)
A.30° B.35° C.40° D.45°
8.如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径等于( )
(第8题图)
A.5 B.6 C.2 D.3
二.填空题(共9小题)
9.如图,某机械传动装置在静止状态时,连杆PA与点A运动所形成的⊙O交于点B,现测得PB=4cm,AB=5cm,⊙O的半径R=4.5cm,此时P点到圆心O的距离是 cm.
(第9题图)
10.如图,⊙O1与⊙O2相交于A、B两点,连接AB,并在其延长线上取点P,过点P作⊙O1、⊙O2的切线PC、PD,切点分别为C、D,若PC=6,则PD= .
(第10题图)
11.已知四边形ABCD是圆内接四边形,两组对边延长后分别交于点E,F,且EA?ED=25,FC?FD=144,则EF= .
12.如图,在△ABC中,∠B=36°,∠ACB=128°,∠CAB的平分线交BC于点M,△ABC的外接圆的切线AN交BC的延长线于点N,则△ANM的最小角等于 .
(第12题图)
13.如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,BP的长为 .
(第13题图)
14.如图,在矩形ABCD中,AB=5,BC=4,以CD为直径作⊙O.将矩形ABCD绕点C旋转,
使所得矩形A′B′CD′的边A′B′与⊙O相切,切点为E,边CD′与⊙O相交于点F,
则CF的长为 .
(第14题图)
15.如图,AT切⊙O于点A,AB是⊙O的直径.若∠ABT=40°,则∠ATB= .
(第15题图)
16.如图,已知∠AOB=30°,在射线OA上取点O1,以O1为圆心的圆与OB相切;在射线O1A上取点O2,以O2为圆心,O2O1为半径的圆与OB相切;在射线O2A上取点O3,以O3为圆心,O3O2为半径的圆与OB相切;…;在射线O9A上取点O10,以O10为圆心,O10O9为半径的圆与OB相切.若⊙O1的半径为1,则⊙O10的半径长是 .
(第16题图)
17.如图,在直角坐标系中,⊙A的圆心A的坐标为(﹣1,0),半径为1,点P为直线y=﹣x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是 .
(第17题图)
三.解答题(共23小题)
18.如图,已知P是⊙O外一点,PS,PT是⊙O的两条切线,过点P作⊙O的割线PAB,交⊙O于A、B两点,并交ST于点C.
求证:.
(第18题图)
19.如图,Rt△BDE中,∠BDE=90°,BC平分∠DBE交DE于点C,AC⊥CB交BE于点A,△ABC的外接圆的半径为r.
(1)若∠E=30°,求证:BC?BD=r?ED;
(2)若BD=3,DE=4,求AE的长.
(第19题图)
20.如图,两个同心圆的圆心是O,大圆的半径为13,小圆的半径为5,AD是大圆的直径.大圆的弦AB,BE分别与小圆相切于点C,F.AD,BE相交于点G,连接BD.
(1)求BD的长;
(2)求∠ABE+2∠D的度数;
(3)求的值.
(第20题图)
21.如图,△ABC内接于⊙O,过点B作⊙O的切线,交于CA的延长线于点E,∠EBC=2∠C.
(1)求证:AB=AC;
(2)当=时,①求tan∠ABE的值;②如果AE=,求AC的值.
(第21题图)
22.如图,⊙Ol和⊙O2内切于点P,过点P的直线交⊙Ol于点D,交⊙O2于点E,DA与⊙O2相切,切点为C.
(1)求证:PC平分∠APD;
(2)求证:PD?PA=PC2+AC?DC;
(3)若PE=3,PA=6,求PC的长.
(第22题图)
参考答案
一.1.A【解析】∵△ABC是一张三角形的纸片,⊙O是它的内切圆,D是其中的一个切点,AD=10cm,∴设E、F分别是⊙O的切点,故DM=MF,FN=EN,AD=AE,∴AM+AN+MN=AD+AE=10+10=20(cm).故选A.
(第1题答图)
【点评】此题主要考查了切线长定理,得出AM+AN+MN=AD+AE是解题的关键.
2.A【解析】如图,若,且AB=10,∴AD=4,BD=6,作AB关于直线BC的对称线段A′B,交半圆于D′,连接AC、CA′,可得A、C、A′三点共线.∵线段A′B与线段AB关于直线BC对称,∴AB=A′B,∴AC=A′C,AD=A′D′=4,A′B=AB=10.而A′C?A′A=A′D′?A′B,即A′C?2A′C=4×10=40.则A′C2=20.又∵A′C2=A′B2﹣CB2,∴20=100﹣CB2,∴CB=4.
故选A.
(第2题图)
【点评】此题将翻折变换、勾股定理、割线定理相结合,考查了同学们的综合应用能力,要善于观察图形的特点,然后做出解答.
3.D【解析】根据切线长定理,得BE=EF,DF=DC=AD=AB=BC.设EF=x,DF=y,则在直角△AED中,AE=y﹣x,AD=CD=y,DE=x+y.根据勾股定理,可得(y﹣x)2+y2=(x+y)2,∴y=4x,∴三角形ADE的周长为12x,直角梯形EBCD的周长为14x,∴两者周长之比为12x:14x=6:7.
故选D.
【点评】此题考查圆的切线长定理,正方形的性质和勾股定理等知识,解答本题关键是运用切线长定理得出EB=EF,DF=DC,从而求解.
4.B【解析】AH?AD=AC?AE=AC?AB?cos∠BAE=(b2+c2﹣a2),同理BH?BE=(a2+c2﹣b2),CH?CF=(a2+b2﹣c2),故AH?AD+BH?BE+CH?CF=(a2+b2+c2).故选B.
【点评】本题主要考查了切割线定理,理解H、D、C、E四点共圆是解决本题的关键.
5.D【解析】过点O作OH∥AC,交AB与点H,交BC于点Z,过点O作OE∥BC,交AB的延长线于点E,连接OM,ON,过点M作MG⊥OH于点G,作NK⊥OE于点K.∵△ACB是等边三角形,∴∠A=∠ACB=∠ABC=60°.∵OE∥BC,∴∠ACB=∠CZO=60°.∴∠HZB=60°.∵OE∥CB,∴∠EOH=∠HZB=60°.∵OC∥AB,∴四边形AHOC是平行四边形,∴∠A=∠COZ=60°,∴△OZC是等边三角形.∵MG⊥OH,NK⊥OH,∴MG,NK均为△OZC的高,∴MG=NK.在Rt△OMG与Rt△ONK中,∵,∴△OMG≌△ONK(HL),∴∠MOG=∠KON,∴∠MON=60°,∴的度数为60°.故选D.
(第5题答图)
【点评】本题考查的是切线的性质,根据题意作出辅助线,构造出平行四边形及等边三角形,利用圆心角与弧的关系求解是解答此题的关键.
6.C【解析】连接DG、AG,作GH⊥AD于点H,连接OD,如图.∵G是BC的中点,∴AG=DG,∴GH垂直平分AD,∴点O在HG上.∵AD∥BC,∴HG⊥BC,∴BC与圆O相切.∵OG=OD,∴点O不是HG的中点,∴圆心O不是AC与BD的交点.而四边形AEFD为⊙O的内接矩形,∴AF与DE的交点是圆O的圆心;∴(1)错误,(2)(3)正确.故选C.
(第6题答图)
【点评】本题考查了三角形内切圆与内心:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.也考查了矩形的性质.
7.D【解析】∵直线AB是⊙O的切线,C为切点,∴∠OCB=90°.∵OD∥AB,∴∠COD=90°,
∴∠CED=∠COD=45°.故选D.
【点评】本题主要考查切线的性质,解题的关键是掌握圆的切线垂直于经过切点的半径及圆周角定理.
8.C【解析】如图作DH⊥AB于点H,连接BD,延长AO交BD于点E.
(第8题答图)
∵菱形ABCD的边AB=20,面积为320,∴AB?DH=320,∴DH=16.在Rt△ADH中,AH==12,∴HB=AB﹣AH=8.在Rt△BDH中,BD==8.设⊙O与AB相切于F,连接OF.∵AD=AB,OA平分∠DAB,∴AE⊥BD.∵∠OAF+∠ABE=90°,∠ABE+∠BDH=90°,
∴∠OAF=∠BDH,∵∠AFO=∠DHB=90°,∴△AOF∽△DBH,∴=,∴=,
∴OF=2.故选C.
【点评】本题考查切线的性质、菱形的性质、勾股定理、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.
二.9.7.5【解析】连接PO交圆于点C,并延长PO交圆于点D.∵PB=4cm,AB=5cm,∴PA=9cm;
由割线定理,得PB?PA=PC?PD;设点P到圆心的距离是xcm,则有(x﹣4.5)(x+4.5)=36,
解得x=7.5cm.故P到O点的距离为7.5cm.
(第9题答图)
【点评】此题要通过作辅助线构造割线,然后运用割线定理列方程求解.
10.6【解析】∵依题意,可得PC2=PB?PA,PD2=PA?PB,∴PC2=PD2.∵PC=6,∴PC=PD=6.
【点评】注意:切割线定理和割线定理必须在同一个圆中运用;这里借助割线PBA建立了两条切线长的相等关系.
11.13【解析】∵∠A=∠BCF=∠CFE+∠CE∴在∠A内作∠EAG交EF于点G,使∠EAG=∠DFE,则∠FAG=∠FEB.在△EAG和△EFD中,∠EAG=∠DFE,∠AEG=∠FED,则△EAG∽△EFD,∴EA:EF=EG:ED,即EG×EF=EA×ED(1).在△EFB和△AFG中,∠FAG=∠FEB,∠AFG=∠EFB,
所以△EFB∽△AFG,∴AF:EF=FG:FB,即FG×EF=AF×BF (2),(1)+(2),得EG×EF+FG×EF=EA×ED+AF×BF,EF×(EG+FG)=EA×ED+AF×BF,即EF2=EA×ED+AF×BF,由割线定理,得到AF×BF=FC×FD,∴EF2=EA×ED+FC×FD=25+144=169,因此EF=13.
(第11题答图)
【点评】本题巧妙地从△EAG∽△EFD和△EFB∽△AFG得到的结论,同切割定理结合起来,从而解得.
12.44°【解析】∵∠B=36°,∠ACB=128°,AM为∠CAB的平分线,∴∠CAM=∠MAB=×(180°﹣36°﹣128°)=8°.∵∠AMC=36°+8°=44°,又AN为切线,∴∠NAC=∠B=36°,∠NAM=44°,∴∠N=180°﹣44°﹣44°=92°,∴△ANM的最小角为44°.
【点评】本题考查了切线的性质、三角形的内角和定理是基础知识比较简单.
13.3或4【解析】如图1中,当⊙P与直线CD相切时,设PC=PM=x.
(第13题答图)
在Rt△PBM中,∵PM2=BM2+PB2,∴x2=42+(8﹣x)2,∴x=5,∴PC=5,BP=BC﹣PC=8﹣5=3.
如图2中当⊙P与直线AD相切时.设切点为K,连接PK,则PK⊥AD,四边形PKDC是矩形.
∴PM=PK=CD=2BM,∴BM=4,PM=8,在Rt△PBM中,PB==4.综上所述,BP的长为3或4.
【点评】本题考查切线的性质、正方形的性质、勾股定理等知识,解题的关键是学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题.
14.4【解析】连接OE,延长EO交CD于点G,作OH⊥B′C于点H,则∠OEB′=∠OHB′=90°.
∵矩形ABCD绕点C旋转所得矩形为A′B′C′D′,∴∠B′=∠B′CD′=90°,AB=CD=5、BC=B′C=4,∴四边形OEB′H和四边形EB′CG都是矩形,OE=OD=OC=2.5,∴B′H=OE=2.5,
∴CH=B′C﹣B′H=1.5,∴CG=B′E=OH===2.∵四边形EB′CG是矩形,∴∠OGC=90°,即OG⊥CD′,∴CF=2CG=4.
(第14题答图)
【点评】本题主要考查圆的切线的判定与性质,解题的关键是掌握矩形的判定与性质、旋转的性质、切线的性质、垂径定理等知识点.
15.50°【解析】∵AT切⊙O于点A,AB是⊙O的直径,∴∠BAT=90°.∵∠ABT=40°,∴∠ATB=50°.
【点评】本题考查切线的性质,解题的关键是根据切线的性质求出∠ATB=90°,本题属于基础题型.
16.29【解析】作O1C、O2D、O3E分别⊥OB.∵∠AOB=30°,∴OO1=2CO1,OO2=2DO2,OO3=2EO3.
∵O1O2=DO2,O2O3=EO3,∴圆的半径呈2倍递增,∴⊙On的半径为2n﹣1 CO1.∵⊙O1的半径为1,
∴⊙O10的半径长=29,
(第16题答图)
【点评】本题考查了圆切线的性质,考查了30°角所对直角边是斜边一半的性质,本题中找出圆半径的规律是解题的关键.
17.2【解析】如图,作AP⊥直线y=﹣x+3,垂足为P,作⊙A的切线PQ,切点为Q,此时切线长PQ最小.∵A的坐标为(﹣1,0),设直线与x轴,y轴分别交于C,B,∴B(0,3),C(4,0),∴OB=3,AC=5,∴BC==5,∴AC=BC,在△APC与△BOC中,,∴△APC≌△BOC,∴AP=OB=3,∴PQ==2.∵PQ2=PA2﹣1,此时PA最小,所以此时切线长PQ也最小,最小值为2.
(第17题答图)
【点评】本题主要考查切线的性质,掌握过切点的半径与切线垂直是解题的关键,用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.
三.18.证明:连PO交ST于点D,则PO⊥ST,连接SO,作OE⊥PB于E,则E为AB中点,
于是.
因为C、E、O、D四点共圆,
所以PC?PE=PD?PO.
又因为Rt△SPD∽Rt△OPS,
所以,
即PS2=PD?PO,
而由切割线定理知,PS2=PA?PB,
所以.
即.
(第18题答图)
【点评】本题主要考查了切割线定理以及三角形相似的证明,注意对比例式的变形是解题关键.
19.(1)证明:取AB中点O,△ABC是Rt△,AB是斜边,O是外接圆心,连接CO,
∴BO=CO,∠BCO=∠OBC.
∵BC是∠DBE平分线,
∴∠DBC=∠CBA,
∴∠OCB=∠DBC,
∴OC∥DB,(内错角相等,两直线平行),
∴,把比例式化为乘积式,得BD?CE=DE?OC.
∵OC=r,
∴BD?CE=DE?r.
∵∠D=90°,∠E=30°,
∴∠DBE=60°,
∴∠CBE=∠DBE=30°,
∴∠CBE=∠E,
∴CE=BC,
∴BC?BD=r?ED.
(2)解:BD=3,DE=4,根据勾股定理,BE=5.
设圆的半径长是r,则OC=OA=r.
∵OC∥DB,
∴△OCE∽△BDE,
∴==,即==,
解得OE=r,CE=r,CH==r.
∵BC平分∠DBE交DE于点C,则△BDC≌△BHC,
∴BH=BD=3,则HE=2.
∴CD=CH=r.
在直角△CHE中,根据勾股定理,得CH2+EH2=CE2,
即(r)2+22=(r)2,解得r=,
则AE=BE﹣2r=5﹣=.
(第19题答图)
【点评】本题考查的是切割线定理,切线的性质定理,勾股定理.
20.解:(1)连接OC,BD.∵AB是小圆的切线,C是切点,
∴OC⊥AB,
∴C是AB的中点.
∵AD是大圆的直径,
∴O是AD的中点.
∴OC是△ABD的中位线.
∴BD=2OC=10.
(2)连接AE.
由(1)知,C是AB的中点.
同理F是BE的中点.
即AB=2BC,BE=2BF,
由切线长定理,得BC=BF.
∴BA=BE.
∴∠BAE=∠E.
∵∠E=∠D,
∴∠ABE+2∠D=∠ABE+∠E+∠BAE=180°.
(3)连接BO.在Rt△OCB中.
∵OB=13,OC=5,
∴BC=12.
由(2)知,∠OBG=∠OBC=∠OAC.
∵∠BGO=∠AGB,
∴△BGO∽△AGB.
∴.
(第20题答图)
【点评】在解本题的过程中要用到切线长定理,中位线定理,相似三角形的判定等知识,要求学生熟练掌握和应用.
21.(1)证明:∵BE切⊙O于点B,
∴∠ABE=∠C.
∵∠EBC=2∠C,即∠ABE+∠ABC=2∠C.
∴∠ABC=∠C.
∴AB=AC.
(2)解:①如图,连接AO,交BC于点F.
∵AB=AC,∴,
∴AO⊥BC,且BF=FC.
∵,∴∴;
设AB=m,BF=2m,
由勾股定理,得AF==;
∴tan∠ABE=tan∠ABF=.
②在△EBA和△ECB中,
∵∠E=∠E,∠EBA=∠ECB,∴△EBA∽△ECB,
∴.
∵,
∴EB=EA.※
由切割线定理,得EB2=EA×EC=EA(EA+AC).
将(※)式代入上式,得EA2=EA(EA+AC);
∵EA≠0,
∴AC=EA=×=4.
(第21题答图)
【点评】本题主要考查了相似三角形的性质,对应边的比相等,以及切割线定理.
22.解:(1)过点P作两圆的公切线PT.
根据弦切角定理,得∠PCD=∠PBC,∠PCB=∠PDC.
∴∠DPC=∠APC,
∴PC平分∠APD;
(2)∵AC?DC=PC?CF,
∴PC2+AC?DC=PC2+PC?CF=PC(PC+CF)=PC?PF.
∵△PDC∽△PFA,
∴PC?PF=PD?PA,
∴PD?PA=PC2+AC?DC;
(3)∵△PCA∽△PEC,
∴=,
即PC2=PA?PE.
∵PE=3,PA=6,
∴PC=3.
(第22题答图)
【点评】本题考查了相似三角形的判定和性质、弦切角定理等知识,综合性强,难度较大.
