沪科版九年级数学下册:24.5三角形的内切圆 同步练习 解析版
文档属性
| 名称 | 沪科版九年级数学下册:24.5三角形的内切圆 同步练习 解析版 |
|
|
| 格式 | zip | ||
| 文件大小 | 227.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-04 00:00:00 | ||
图片预览



文档简介
24.5 三角形的内切圆
一.选择题(共9小题)
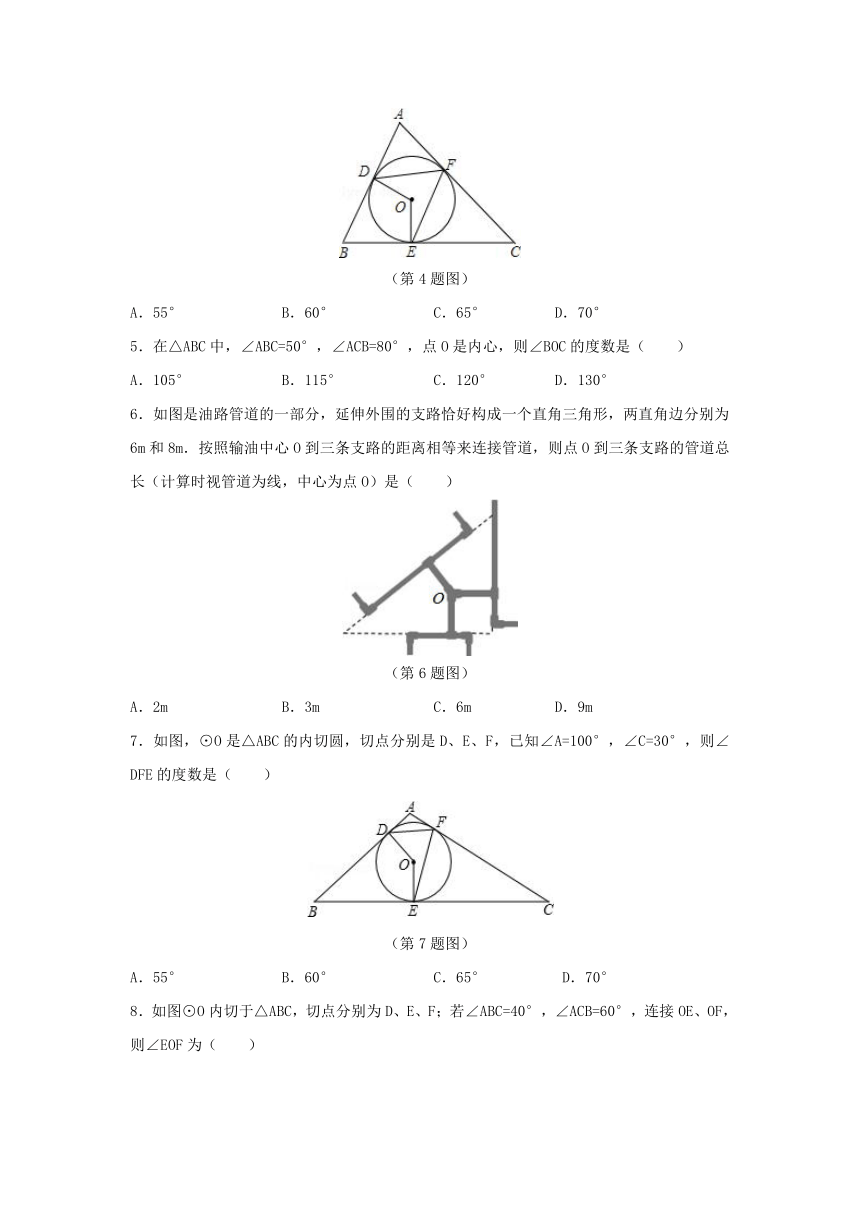
1.已知在△ABC中,∠C=90°,BC=a,CA=b,AB=c,⊙O与三角形的边相切,则下列选项,⊙O的半径为的是( )
A B
C D
2.如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC=( )
(第2题图)
A.100° B.75° C.115° D.105°
3.△ABC的三边长分别为6、8、10,则其内切圆和外接圆的半径分别是( )
A.2,5 B.1,5 C.4,5 D.4,10
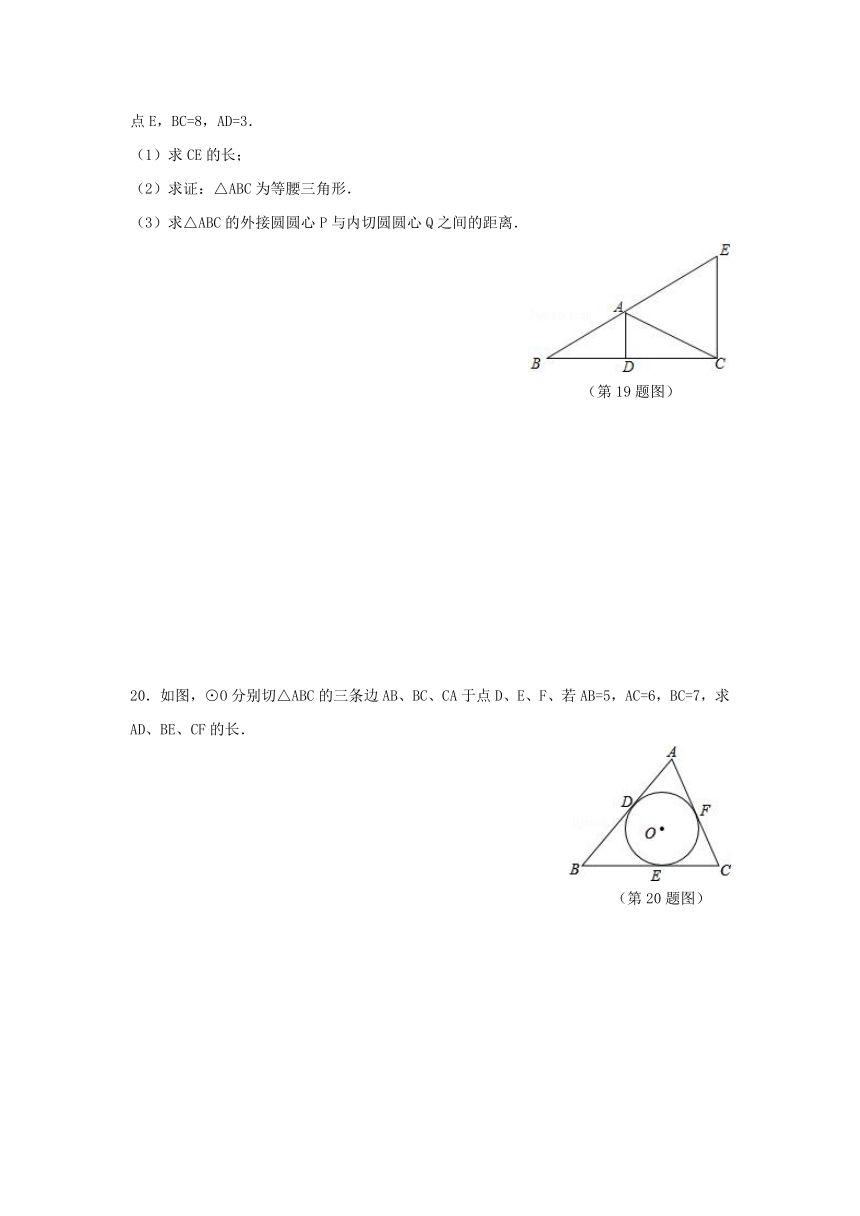
4.如图,⊙O是△ABC内切圆,切点分别是D、E、F,已知∠B=50°,则∠DFE的度数是( )
(第4题图)
A.55° B.60° C.65° D.70°
5.在△ABC中,∠ABC=50°,∠ACB=80°,点O是内心,则∠BOC的度数是( )
A.105° B.115° C.120° D.130°
6.如图是油路管道的一部分,延伸外围的支路恰好构成一个直角三角形,两直角边分别为6m和8m.按照输油中心O到三条支路的距离相等来连接管道,则点O到三条支路的管道总长(计算时视管道为线,中心为点O)是( )
(第6题图)
A.2m B.3m C.6m D.9m
7.如图,⊙O是△ABC的内切圆,切点分别是D、E、F,已知∠A=100°,∠C=30°,则∠DFE的度数是( )
(第7题图)
A.55° B.60° C.65° D.70°
8.如图⊙O内切于△ABC,切点分别为D、E、F;若∠ABC=40°,∠ACB=60°,连接OE、OF,则∠EOF为( )
(第8题图)
A.80° B.100° C.120° D.140°
9.等边三角形的周长为18,则它的内切圆半径是( )
A.2 B.3 C. D.
二.填空题(共9小题)
10.如图所示,设I是△ABC的内心(三条角平分线的交点),AI的延长线交BC边于点D,交△ABC的外接圆于点E,若IE=4,AE=8,则线段DE的长是 .
(第10题图)
11.如图,在平面直角坐标系xOy中,点A在第一象限,点B在x轴的正半轴上,∠OAB=90°,⊙P1是△OAB的内切圆,且P1的坐标为(3,1),则OB的长为 .
(第11题图)
12.Rt△ABC的两条直角边长分别为3cm、4cm,则该三角形的内切圆的面积为 .
13.已知O为△ABC的内心,且∠BOC=130°,则∠A= .
(第13题图)
14.如图,⊙I是直角△ABC的内切圆,切点为D、E、F,若AF=10,BE=3,则△ABC的面积为 .
(第14题图)
15.已知,在△ABC中,∠C=90°,斜边的长为7.5,两条直角边的长分别是关于x的方程x2﹣3(m+)x+9m=0的两个根,则△ABC的内切圆面积是 .
16.如图,点I是△ABC的内切圆的圆心,若∠BIC=130°,则∠A的度数是 .
(第16题图)
17.如图,Rt△ABC中,∠C=90°,AC=6,BC=8.则△ABC的内切圆的半径r= .
(第17题图)
18.如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC= 度.
(第18题图)
三.解答题(共3小题)
19.如图,在△ABC中,AD是边BC上的中线,∠BAD=∠CAD,CE∥AD,CE交BA的延长线于点E,BC=8,AD=3.
(1)求CE的长;
(2)求证:△ABC为等腰三角形.
(3)求△ABC的外接圆圆心P与内切圆圆心Q之间的距离.
(第19题图)
20.如图,⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F、若AB=5,AC=6,BC=7,求AD、BE、CF的长.
(第20题图)
21.如图,O是△ABC的内切圆的圆心,∠BAC=80°,求∠BOC的度数.
(第21题图)
参考答案
一.1.D【解析】①∵⊙O是△ABC的内切圆,∴⊙O的半径=,∴A不正确;②∵⊙O与AB,BC相切,∴r2+(c﹣a)2=(b﹣r)2,∴r=,∴B不正确;③∵⊙O与AC,BC相切,圆心在AB上,∴=,∴r=,∴C正确,④∵⊙O与AB,AC相切,圆心在BC 上,∴(a﹣r)2=r2+(c﹣b)2,∴r=,∴D不正确.故选D.
【点评】本题考查了三角形的内切圆,切线长定理,勾股定理的应用,正确弄清圆与三角形的位置关系是解决本题的关键.
2.C【解析】∵⊙O是△ABC的内切圆,∴∠OBC=∠ABC=25°,∠OCB=∠ACB=40°.∴∠BOC=180°﹣25°﹣40°=115°.故选C.
【点评】本题主要考查的是三角形的内切圆与内心,明确三角形的内心是三角形三条内角平分线的交点是解题的关键.
3.A【解析】∵62+82=102,∴△ABC为直角三角形,∴△ABC的内切圆的半径==2,
△ABC的外接圆的半径==5.故选A.
【点评】本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.也考查了勾股定理的逆定理.记住直角边为a、b,斜边为c的三角形的内切圆半径为.
4.C【解析】∵⊙O是△ABC内切圆,D、E是切点,∴∠ODB=∠OEB=90°,∴∠DOE=360°﹣∠ODB﹣∠OEB﹣∠B=130°,∴∠DFE=∠DOE=65°.故选C.
【点评】本题考查了三角形的内切圆与内心、圆周角定理、四边形内角和定理;熟练掌握圆周角定理,并能进行推理计算是解决问题的关键.
5.B【解析】∵点O是内心,∠ABC=50°,∠ACB=80°,∴∠OBC=∠ABC=25°,∠OCB=∠ACB=40°,∴∠BOC=180°﹣∠OBC﹣∠OCB=180°﹣25°﹣40°=115°.故选B.
【点评】本题考查了对三角形的内切圆与内心的应用,注意:三角形的内心是三角形的三个内角的角平分线的交点.
6.C【解析】在直角△ABC中,BC=8m,AC=6m.则AB===10.∵中心O到三条支路的距离相等,设距离是r.△ABC的面积=△AOB的面积+△BOC的面积+△AOC的面积,即AC?BC=AB?r+BC?r+AC?r,即6×8=10r+8r+6r∴r==2.故点O到三条支路的管道总长是2×3=6m.故选C.
(第6题答图)
【点评】本题主要考查了三角形的内心的性质,三角形的内心到三角形的各边的距离相等,利用三角形的面积的关系求解是解题的关键.
7.C【解析】∵∠A=100°,∠C=30°,∴∠B=50°.∵∠BDO=∠BEO,∴∠DOE=130°,∴∠DFE=65°.故选C.
【点评】熟练运用三角形的内角和定理、四边形的内角和定理以及切线的性质定理、圆周角定理.
8.B【解析】∵∠ABC=40°,∠ACB=60°,∴∠A=80°,∴∠EOF=180°﹣80°=100°.故选B.
【点评】此题要熟练运用切线的性质定理、四边形的内角和定理以及三角形的内角和定理.
9.C【解析】如答图,连接OB,OD.∵等边△ABC是⊙O的内接圆,△ABC的周长为18,∴∠ABC=60°,BC=6,∴OD⊥BC,∠OBD=∠ABC=×60°=30°,BD=BC=3,∴OD=BD?tan∠OBD=3×=.∴它的内切圆半径是.故选C.
(第9题答图)
【点评】此题考查了正三角形的性质与三角形内接圆的性质.此题难度不大,解题的关键是注意数形结合思想的应用,注意辅助线的作法.
二.10.2【解析】连接IB,如答图.∵I是△ABC的内心,∴∠BAD=∠CAD,∠ABI=∠IBD.又∵∠BIE=∠BAD+∠ABI=∠CAD+∠IBD=∠IBD+∠DBE=∠IBE,∴BE=IE.在△BED和△AEB中,∠EBD=∠CAD=∠BAD,∠BED=∠AEB,∴△BED∽△AEB,∴.∵IE=4,AE=8,∴BE=4,即DE=.
(第10题答图)
【点评】本题考查三角形的内心与外心、三角形相似,解题的关键是明确题意,找出所求问题需要的条件.
11.5【解析】如答图,设切点分别为E、Q、H,连接P1H,P1Q,P1E.则P1H⊥OB,P1Q⊥AO,P1E⊥AB.∵⊙P1是△OAB的内切圆,且P1的坐标为(3,1),∴P1H=P1Q=P1E=1,OQ=OH=3,BH=BE.∵∠OAB=90°,∴四边形AQP1E为正方形,∴AQ=AE=P1Q=1,∴AO=OQ+AQ=3+1=4.在Rt△ABO中,OB2=OA2+AB2,∴(3+BH)2=42+(1+BH)2,解得BH=2,∴OB=OH+BH=3+2=5.
(第11题答图)
【点评】本题考查了圆的综合题:熟练运用圆的切线性质和切线长定理进行几何证明;会运用勾股定理进行几何计算;常用三角形全等解决线段相等的问题.
12.πcm2【解析】斜边==5,则该三角形的内切圆的半径==1,所以该三角形的内切圆的面积为π?12=π(cm2).
【点评】本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.记住直角三角形的内切圆的半径=(a、b为直角边,c为斜边).
13.80°【解析】∵OB、OC是∠ABC、∠ACB的角平分线,∴∠OBC+∠OCB=180°﹣130°=50°,而∠OBC+∠OCB=(∠ABC+∠ACB)=50°,∴∠ABC+∠ACB=100°,∴∠BAC=180°﹣100°=80°.
【点评】本题考查了三角形内心的性质:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.
14.30【解析】∵⊙I是直角△ABC的内切圆,∴BD=BE,AF=AD.∵AF=10,BE=3,∴BD=3,AD=10.设CE=x,则CF=x,在Rt△ABC中,AC2+BC2=AB2,∴(x+10)2+(x+3)2=132,解得x1=﹣15,x2=2,∴CE=2,∴BC=5,AC=12,∴S△ABC=AC?BC=×5×12=30.
【点评】本题考查了三角形的内切圆与内心,以及切线长定理,勾股定理,熟记切线长定理的内容是解题的关键.
15.π【解析】设两直角边长分别为a、b.∵两条直角边的长分别是关于x的方程x2﹣3(m+)x+9m=0的两个根,∴a+b=3(m+),ab=9m.∵直角三角形的斜边为7.5,∴a2+b2=7.52,∴(a+b)2﹣2ab=,∴9(m+)2﹣18m=,解得m=﹣2或3,经检验m=﹣2不合题意,即m只能为3,∴a+b=.∵直角三角形的内切圆的半径r=(a+b+c),∴r=,∴△ABC的内切圆的面积为π.
【点评】本题考查了三角形的内切圆,勾股定理,根与系数的关系的应用,能求出m的值是解此题的关键.
16.80°【解析】∵点I是△ABC的内切圆的圆心,∴∠IAB+∠IBA=(∠BAC+∠CBA),∵∠BIC=130°,∴∠IAB+∠IBA=180°﹣∠BIC.∵∠BIC=130°,∴∠BAC+∠CBA=2(∠IAB+∠IBA)=100°,∴∠A=180°﹣100°=80°,
【点评】本题考查了三角形的内切圆和内心的定义,是基础知识比较简单.
17.【解析】如答图.在Rt△ABC,∠C=90°,AC=6,BC=8;根据勾股定理AB==10;
四边形OECF中,OE=OF,∠OEC=∠OFC=∠C=90°,∴四边形OECF是正方形;由切线长定理,得AD=AF,BD=BE,CE=CF;∴CE=CF=(AC+BC﹣AB),即r=(6+8﹣10)=2.
(第17题答图)
【点评】此题主要考查直角三角形内切圆的性质及半径的求法.
18.【解析】∵OB、OC是∠ABC、∠ACB的角平分线,∴∠OBC+∠OCB=(∠ABC+∠ACB)=(50°+80°)=65°,∴∠BOC=180°﹣65°=115°.
【点评】本题通过三角形的内切圆,考查切线的性质.
三.19.(1)解:∵AD是边BC上的中线,
∴BD=CD.
∵CE∥AD,
∴AD为△BCE的中位线,
∴CE=2AD=6;
(2)证明:∵CE∥AD,
∴∠BAD=∠E,∠CAD=∠ACE,
而∠BAD=∠CAD,
∴∠ACE=∠E,
∴AE=AC,
而AB=AE,
∴AB=AC,
∴△ABC为等腰三角形.
(3)如答图,连接BP、BQ、CQ.
在Rt△ABD中,AB==5,
设⊙P的半径为R,⊙Q的半径为r,
在Rt△PBD中,(R﹣3)2+42=R2,解得R=,
∴PD=PA﹣AD=﹣3=.
∵S△ABQ+S△BCQ+S△ACQ=S△ABC,
∴?r?5+?r?8+?r?5=?3?8,解得r=,
即QD=,
∴PQ=PD+QD=+=.
答:△ABC的外接圆圆心P与内切圆圆心Q之间的距离为.
(第19题图)
【点评】本题考查了三角形内切圆与内心:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.也考查了等腰三角形的判定与性质和三角形的外接圆.
20.解:假设AD=x.
∵⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F;
∴根据切线长定理得出AD=AF,BD=BE,EC=FC,
∴AF=x.
∵AB=5,AC=6,BC=7,
∴BE=BD=AB﹣AD=5﹣x,FC=EC=AC﹣AF=6﹣x,
∴BC=BE+EC=5﹣x+6﹣x=7,
解得x=2.
∴AD=2,BE=BD=5﹣2=3,CF=AC﹣AF=6﹣2=4.
【点评】此题主要考查了切线长定理以及三角形内切圆的性质,用已知数和未知数表示所有的切线长,再进一步列方程求解是解题关键.
21.解:∵∠BAC=80°,
∴∠ABC+∠ACB=180°﹣80°=100°.
∵点O是△ABC的内切圆的圆心,
∴BO,CO分别为∠ABC,∠BCA的角平分线,
∴∠OBC+∠OCB=50°,
∴∠BOC=130°.
【点评】此题主要考查了三角形的内切圆与内心,准确运用三角形内心的性质,是解决问题的关键.
一.选择题(共9小题)
1.已知在△ABC中,∠C=90°,BC=a,CA=b,AB=c,⊙O与三角形的边相切,则下列选项,⊙O的半径为的是( )
A B
C D
2.如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC=( )
(第2题图)
A.100° B.75° C.115° D.105°
3.△ABC的三边长分别为6、8、10,则其内切圆和外接圆的半径分别是( )
A.2,5 B.1,5 C.4,5 D.4,10
4.如图,⊙O是△ABC内切圆,切点分别是D、E、F,已知∠B=50°,则∠DFE的度数是( )
(第4题图)
A.55° B.60° C.65° D.70°
5.在△ABC中,∠ABC=50°,∠ACB=80°,点O是内心,则∠BOC的度数是( )
A.105° B.115° C.120° D.130°
6.如图是油路管道的一部分,延伸外围的支路恰好构成一个直角三角形,两直角边分别为6m和8m.按照输油中心O到三条支路的距离相等来连接管道,则点O到三条支路的管道总长(计算时视管道为线,中心为点O)是( )
(第6题图)
A.2m B.3m C.6m D.9m
7.如图,⊙O是△ABC的内切圆,切点分别是D、E、F,已知∠A=100°,∠C=30°,则∠DFE的度数是( )
(第7题图)
A.55° B.60° C.65° D.70°
8.如图⊙O内切于△ABC,切点分别为D、E、F;若∠ABC=40°,∠ACB=60°,连接OE、OF,则∠EOF为( )
(第8题图)
A.80° B.100° C.120° D.140°
9.等边三角形的周长为18,则它的内切圆半径是( )
A.2 B.3 C. D.
二.填空题(共9小题)
10.如图所示,设I是△ABC的内心(三条角平分线的交点),AI的延长线交BC边于点D,交△ABC的外接圆于点E,若IE=4,AE=8,则线段DE的长是 .
(第10题图)
11.如图,在平面直角坐标系xOy中,点A在第一象限,点B在x轴的正半轴上,∠OAB=90°,⊙P1是△OAB的内切圆,且P1的坐标为(3,1),则OB的长为 .
(第11题图)
12.Rt△ABC的两条直角边长分别为3cm、4cm,则该三角形的内切圆的面积为 .
13.已知O为△ABC的内心,且∠BOC=130°,则∠A= .
(第13题图)
14.如图,⊙I是直角△ABC的内切圆,切点为D、E、F,若AF=10,BE=3,则△ABC的面积为 .
(第14题图)
15.已知,在△ABC中,∠C=90°,斜边的长为7.5,两条直角边的长分别是关于x的方程x2﹣3(m+)x+9m=0的两个根,则△ABC的内切圆面积是 .
16.如图,点I是△ABC的内切圆的圆心,若∠BIC=130°,则∠A的度数是 .
(第16题图)
17.如图,Rt△ABC中,∠C=90°,AC=6,BC=8.则△ABC的内切圆的半径r= .
(第17题图)
18.如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC= 度.
(第18题图)
三.解答题(共3小题)
19.如图,在△ABC中,AD是边BC上的中线,∠BAD=∠CAD,CE∥AD,CE交BA的延长线于点E,BC=8,AD=3.
(1)求CE的长;
(2)求证:△ABC为等腰三角形.
(3)求△ABC的外接圆圆心P与内切圆圆心Q之间的距离.
(第19题图)
20.如图,⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F、若AB=5,AC=6,BC=7,求AD、BE、CF的长.
(第20题图)
21.如图,O是△ABC的内切圆的圆心,∠BAC=80°,求∠BOC的度数.
(第21题图)
参考答案
一.1.D【解析】①∵⊙O是△ABC的内切圆,∴⊙O的半径=,∴A不正确;②∵⊙O与AB,BC相切,∴r2+(c﹣a)2=(b﹣r)2,∴r=,∴B不正确;③∵⊙O与AC,BC相切,圆心在AB上,∴=,∴r=,∴C正确,④∵⊙O与AB,AC相切,圆心在BC 上,∴(a﹣r)2=r2+(c﹣b)2,∴r=,∴D不正确.故选D.
【点评】本题考查了三角形的内切圆,切线长定理,勾股定理的应用,正确弄清圆与三角形的位置关系是解决本题的关键.
2.C【解析】∵⊙O是△ABC的内切圆,∴∠OBC=∠ABC=25°,∠OCB=∠ACB=40°.∴∠BOC=180°﹣25°﹣40°=115°.故选C.
【点评】本题主要考查的是三角形的内切圆与内心,明确三角形的内心是三角形三条内角平分线的交点是解题的关键.
3.A【解析】∵62+82=102,∴△ABC为直角三角形,∴△ABC的内切圆的半径==2,
△ABC的外接圆的半径==5.故选A.
【点评】本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.也考查了勾股定理的逆定理.记住直角边为a、b,斜边为c的三角形的内切圆半径为.
4.C【解析】∵⊙O是△ABC内切圆,D、E是切点,∴∠ODB=∠OEB=90°,∴∠DOE=360°﹣∠ODB﹣∠OEB﹣∠B=130°,∴∠DFE=∠DOE=65°.故选C.
【点评】本题考查了三角形的内切圆与内心、圆周角定理、四边形内角和定理;熟练掌握圆周角定理,并能进行推理计算是解决问题的关键.
5.B【解析】∵点O是内心,∠ABC=50°,∠ACB=80°,∴∠OBC=∠ABC=25°,∠OCB=∠ACB=40°,∴∠BOC=180°﹣∠OBC﹣∠OCB=180°﹣25°﹣40°=115°.故选B.
【点评】本题考查了对三角形的内切圆与内心的应用,注意:三角形的内心是三角形的三个内角的角平分线的交点.
6.C【解析】在直角△ABC中,BC=8m,AC=6m.则AB===10.∵中心O到三条支路的距离相等,设距离是r.△ABC的面积=△AOB的面积+△BOC的面积+△AOC的面积,即AC?BC=AB?r+BC?r+AC?r,即6×8=10r+8r+6r∴r==2.故点O到三条支路的管道总长是2×3=6m.故选C.
(第6题答图)
【点评】本题主要考查了三角形的内心的性质,三角形的内心到三角形的各边的距离相等,利用三角形的面积的关系求解是解题的关键.
7.C【解析】∵∠A=100°,∠C=30°,∴∠B=50°.∵∠BDO=∠BEO,∴∠DOE=130°,∴∠DFE=65°.故选C.
【点评】熟练运用三角形的内角和定理、四边形的内角和定理以及切线的性质定理、圆周角定理.
8.B【解析】∵∠ABC=40°,∠ACB=60°,∴∠A=80°,∴∠EOF=180°﹣80°=100°.故选B.
【点评】此题要熟练运用切线的性质定理、四边形的内角和定理以及三角形的内角和定理.
9.C【解析】如答图,连接OB,OD.∵等边△ABC是⊙O的内接圆,△ABC的周长为18,∴∠ABC=60°,BC=6,∴OD⊥BC,∠OBD=∠ABC=×60°=30°,BD=BC=3,∴OD=BD?tan∠OBD=3×=.∴它的内切圆半径是.故选C.
(第9题答图)
【点评】此题考查了正三角形的性质与三角形内接圆的性质.此题难度不大,解题的关键是注意数形结合思想的应用,注意辅助线的作法.
二.10.2【解析】连接IB,如答图.∵I是△ABC的内心,∴∠BAD=∠CAD,∠ABI=∠IBD.又∵∠BIE=∠BAD+∠ABI=∠CAD+∠IBD=∠IBD+∠DBE=∠IBE,∴BE=IE.在△BED和△AEB中,∠EBD=∠CAD=∠BAD,∠BED=∠AEB,∴△BED∽△AEB,∴.∵IE=4,AE=8,∴BE=4,即DE=.
(第10题答图)
【点评】本题考查三角形的内心与外心、三角形相似,解题的关键是明确题意,找出所求问题需要的条件.
11.5【解析】如答图,设切点分别为E、Q、H,连接P1H,P1Q,P1E.则P1H⊥OB,P1Q⊥AO,P1E⊥AB.∵⊙P1是△OAB的内切圆,且P1的坐标为(3,1),∴P1H=P1Q=P1E=1,OQ=OH=3,BH=BE.∵∠OAB=90°,∴四边形AQP1E为正方形,∴AQ=AE=P1Q=1,∴AO=OQ+AQ=3+1=4.在Rt△ABO中,OB2=OA2+AB2,∴(3+BH)2=42+(1+BH)2,解得BH=2,∴OB=OH+BH=3+2=5.
(第11题答图)
【点评】本题考查了圆的综合题:熟练运用圆的切线性质和切线长定理进行几何证明;会运用勾股定理进行几何计算;常用三角形全等解决线段相等的问题.
12.πcm2【解析】斜边==5,则该三角形的内切圆的半径==1,所以该三角形的内切圆的面积为π?12=π(cm2).
【点评】本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.记住直角三角形的内切圆的半径=(a、b为直角边,c为斜边).
13.80°【解析】∵OB、OC是∠ABC、∠ACB的角平分线,∴∠OBC+∠OCB=180°﹣130°=50°,而∠OBC+∠OCB=(∠ABC+∠ACB)=50°,∴∠ABC+∠ACB=100°,∴∠BAC=180°﹣100°=80°.
【点评】本题考查了三角形内心的性质:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.
14.30【解析】∵⊙I是直角△ABC的内切圆,∴BD=BE,AF=AD.∵AF=10,BE=3,∴BD=3,AD=10.设CE=x,则CF=x,在Rt△ABC中,AC2+BC2=AB2,∴(x+10)2+(x+3)2=132,解得x1=﹣15,x2=2,∴CE=2,∴BC=5,AC=12,∴S△ABC=AC?BC=×5×12=30.
【点评】本题考查了三角形的内切圆与内心,以及切线长定理,勾股定理,熟记切线长定理的内容是解题的关键.
15.π【解析】设两直角边长分别为a、b.∵两条直角边的长分别是关于x的方程x2﹣3(m+)x+9m=0的两个根,∴a+b=3(m+),ab=9m.∵直角三角形的斜边为7.5,∴a2+b2=7.52,∴(a+b)2﹣2ab=,∴9(m+)2﹣18m=,解得m=﹣2或3,经检验m=﹣2不合题意,即m只能为3,∴a+b=.∵直角三角形的内切圆的半径r=(a+b+c),∴r=,∴△ABC的内切圆的面积为π.
【点评】本题考查了三角形的内切圆,勾股定理,根与系数的关系的应用,能求出m的值是解此题的关键.
16.80°【解析】∵点I是△ABC的内切圆的圆心,∴∠IAB+∠IBA=(∠BAC+∠CBA),∵∠BIC=130°,∴∠IAB+∠IBA=180°﹣∠BIC.∵∠BIC=130°,∴∠BAC+∠CBA=2(∠IAB+∠IBA)=100°,∴∠A=180°﹣100°=80°,
【点评】本题考查了三角形的内切圆和内心的定义,是基础知识比较简单.
17.【解析】如答图.在Rt△ABC,∠C=90°,AC=6,BC=8;根据勾股定理AB==10;
四边形OECF中,OE=OF,∠OEC=∠OFC=∠C=90°,∴四边形OECF是正方形;由切线长定理,得AD=AF,BD=BE,CE=CF;∴CE=CF=(AC+BC﹣AB),即r=(6+8﹣10)=2.
(第17题答图)
【点评】此题主要考查直角三角形内切圆的性质及半径的求法.
18.【解析】∵OB、OC是∠ABC、∠ACB的角平分线,∴∠OBC+∠OCB=(∠ABC+∠ACB)=(50°+80°)=65°,∴∠BOC=180°﹣65°=115°.
【点评】本题通过三角形的内切圆,考查切线的性质.
三.19.(1)解:∵AD是边BC上的中线,
∴BD=CD.
∵CE∥AD,
∴AD为△BCE的中位线,
∴CE=2AD=6;
(2)证明:∵CE∥AD,
∴∠BAD=∠E,∠CAD=∠ACE,
而∠BAD=∠CAD,
∴∠ACE=∠E,
∴AE=AC,
而AB=AE,
∴AB=AC,
∴△ABC为等腰三角形.
(3)如答图,连接BP、BQ、CQ.
在Rt△ABD中,AB==5,
设⊙P的半径为R,⊙Q的半径为r,
在Rt△PBD中,(R﹣3)2+42=R2,解得R=,
∴PD=PA﹣AD=﹣3=.
∵S△ABQ+S△BCQ+S△ACQ=S△ABC,
∴?r?5+?r?8+?r?5=?3?8,解得r=,
即QD=,
∴PQ=PD+QD=+=.
答:△ABC的外接圆圆心P与内切圆圆心Q之间的距离为.
(第19题图)
【点评】本题考查了三角形内切圆与内心:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.也考查了等腰三角形的判定与性质和三角形的外接圆.
20.解:假设AD=x.
∵⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F;
∴根据切线长定理得出AD=AF,BD=BE,EC=FC,
∴AF=x.
∵AB=5,AC=6,BC=7,
∴BE=BD=AB﹣AD=5﹣x,FC=EC=AC﹣AF=6﹣x,
∴BC=BE+EC=5﹣x+6﹣x=7,
解得x=2.
∴AD=2,BE=BD=5﹣2=3,CF=AC﹣AF=6﹣2=4.
【点评】此题主要考查了切线长定理以及三角形内切圆的性质,用已知数和未知数表示所有的切线长,再进一步列方程求解是解题关键.
21.解:∵∠BAC=80°,
∴∠ABC+∠ACB=180°﹣80°=100°.
∵点O是△ABC的内切圆的圆心,
∴BO,CO分别为∠ABC,∠BCA的角平分线,
∴∠OBC+∠OCB=50°,
∴∠BOC=130°.
【点评】此题主要考查了三角形的内切圆与内心,准确运用三角形内心的性质,是解决问题的关键.
