新版沪科版2019_2020学年九年级数学下册第24章圆24.7弧长与扇形面积作业设计(含答案)
文档属性
| 名称 | 新版沪科版2019_2020学年九年级数学下册第24章圆24.7弧长与扇形面积作业设计(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 261.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-04 00:00:00 | ||
图片预览




文档简介
24.7 弧长与扇形面积
一.选择题(共10小题)
1.下列各结论,正确的为( )
A.圆心角相等的两个扇形相同
B.圆心角相等的两个扇形的面积相等
C.两个面积相等的扇形的圆心角相等
D.同圆或等圆中面积相等的两个扇形的圆心角相等
2.若一个扇形的面积是相应圆的面积的,则它的圆心角为( )
A.150° B.120° C.90° D.60°
3.如果圆锥的高为3cm,母线长为5cm,则圆锥的侧面积是( )
A.16πcm2 B.20πcm2 C.28πcm2 D.36πcm2
4.扇形的周长为16,圆心角为120°,则扇形的面积为( )
A.16 B.32 C.64 D.16π
5.一条圆弧所对的圆心角等于240°,它的长度等于半径为4cm的圆的周长,则这条弧所在的半径为( )
A.3cm B.4cm C.5cm D.6cm
6.圆锥的轴截面是一个等腰三角形,它的面积是10cm2,底边上的高线是5cm,则圆锥的侧面展开图的弧长等于( )
A.8π cm B.4π cm C.8 cm D.4 cm
7.若圆锥的侧面积为12π cm2,它的底面半径为3cm,则此圆锥的母线长为( )
A.4π cm B.4 cm C.2π cm D.2 cm
8.如图,半径为1cm,圆心角为90°的扇形OAB中,分别以OA,OB为直径作半圆,则图中阴影部分的面积为( )
(第8题图)
A.πcm2 B.πcm2 C.cm2 D.cm2
9.一个圆锥和一个圆柱的底面半径相等,且它们的高都等于它们的底面半径,那么它们的侧面积之比为( )
A. B. C. D.
10.两个圆锥,其中一个底面圆的半径为4m,高为3m,另一个底面圆的半径为3m,高为4m,那么这两个圆锥的侧面积( )
A.相等 B.底面圆的半径大的侧面积大
C.底面圆的半径小的侧面积大 D.不能确定
二.填空题(共15小题)
11.若一扇形的面积为100πcm2,此扇形所在圆的半径为50cm,则扇形的圆心角的度数
为 °.
12.如图,阴影部分的图形叫 ,若圆的半径是1,估计它的面积约为 (结果用π表示)
(第12题图)
13.圆锥的底面半径为6cm,母线长为10cm,则它的侧面展开图的圆心角等于 ,表面积为 ;
14.填表:
半径r 圆心角的度数n 弧长l
10 36°
5 2π
120° 12π
(圆周率用π表示即可)
15.一个圆柱的侧面积为120πcm2,高为10cm,则它的底面圆的半径为 .
16.若一个扇形的弧长是8πcm,扇形的面积为48πcm2,则半径是 .
17.如图,在⊙O中,∠AOB=60°,AB=3cm,则劣弧AB的长为 cm.
(第17题图)
18.如图,将一个半径为4cm的半圆绕直径AB的一个端点A旋转40°,那么图中阴影部分的面积为 cm2.
(第18题图)
19.若面积为54πcm2的扇形的半径为18cm,则该扇形的圆心角的度数是 .
20.弧长的计算:如果弧长为l,圆心角的度数为n,圆的半径为r,那么弧长l= .
21.一条弧所对的圆心角是90°,半径是R,则这条弧长为 .
22.扇形的圆心角的度数为60°,面积为6π,则扇形的周长为 .
23.如果圆弧的度数扩大2倍,半径为原来的,则弧长与原弧长的比为 .
24.如图,正方形ABCD边长为a,那么阴影部分的面积S是 .
(第24题图)
25.填表:
半径r 圆心角的度数n 弧长l 扇形面积s
10 36°
6 6π
2 6π
π 4π
三.解答题(共7小题)
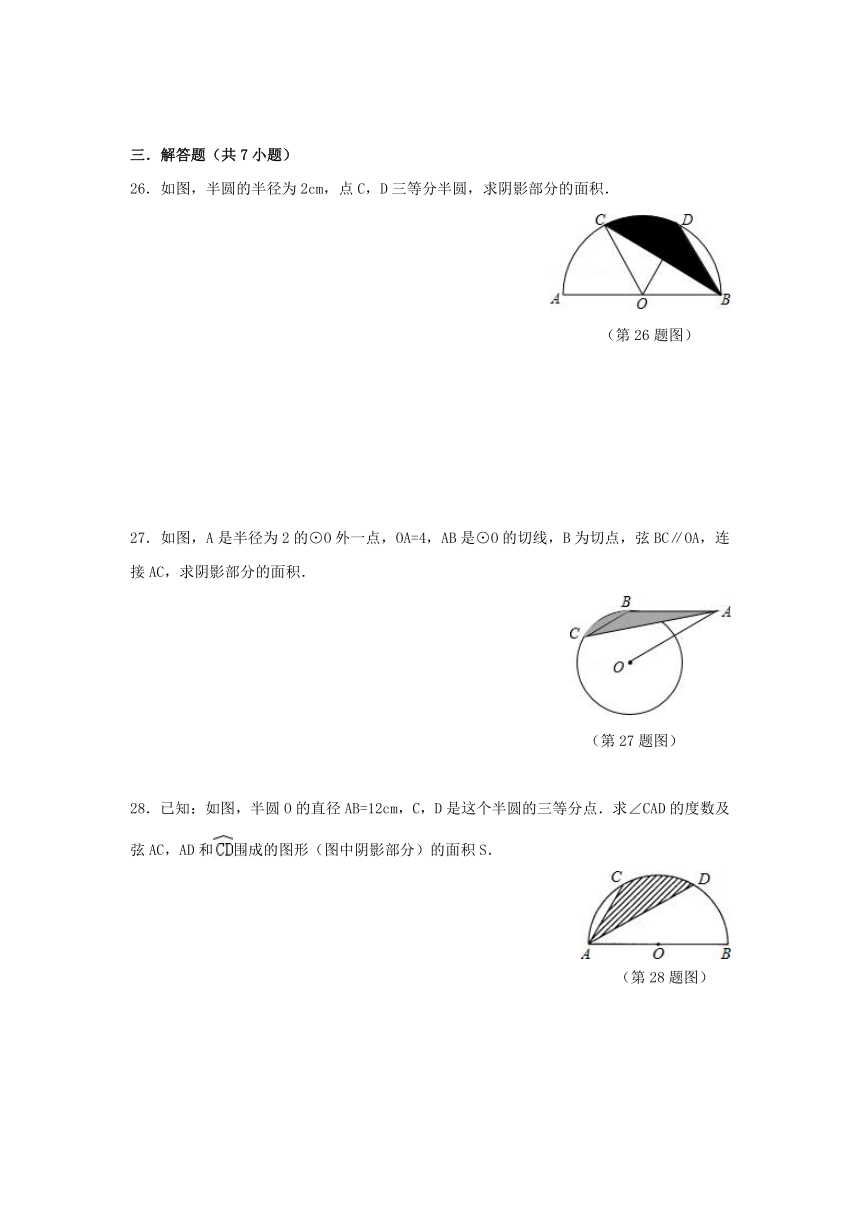
26.如图,半圆的半径为2cm,点C,D三等分半圆,求阴影部分的面积.
(第26题图)
27.如图,A是半径为2的⊙O外一点,OA=4,AB是⊙O的切线,B为切点,弦BC∥OA,连接AC,求阴影部分的面积.
(第27题图)
28.已知:如图,半圆O的直径AB=12cm,C,D是这个半圆的三等分点.求∠CAD的度数及弦AC,AD和围成的图形(图中阴影部分)的面积S.
(第28题图)
29.如图所示,一个半径为的圆过一个半径为2的圆的圆心,则图中阴影部分的面积是多少?
(第29题图)
30.圆心角都是90°的扇形OAB与扇形OCD按如图所示的方式叠放在一起,连结AC,BD.若AO=3cm,OC=1cm,求阴影部分的面积.
(第30题图)
31.如图所示,C,D是以AB为直径的半圆上的三等分点,半径为R,求图中阴影部分的面积.
(第31题图)
32.牧民居住的蒙古包的形状是一个圆柱与圆锥的组合体,尺寸如图所示,请你算出要搭建这样一个蒙古包至少需要多少平方米的蓬布?(π取3.14,结果保留一位小数)
(第32题图)
参考答案
一.1.D【解析】因为不是在同一个圆中的扇形的面积和圆心角都无法比较,故可以排除A,B,C, 而对于同一个圆中,扇形的面积为s=lα2,其中l为圆的半径,α为圆心角.故选D.
【点评】本题涉及圆和圆心角的相应知识,难度一般.
2.C【解析】设圆的面积=πr2,则扇形的面积==,解得n=90°.故选C.
【点评】本题主要是利用扇形的面积是相应圆的面积的关系,列出等式,求得圆心角的度数.
3.B【解析】圆锥的高为3cm,母线长为5cm,由勾股定理,得底面半径为4cm,底面周长为8πcm,侧面展开图的面积为×8π×5=20πcm2.故选B.
【点评】本题利用了勾股定理,圆的周长公式和扇形的面积公式求解.
4.A【解析】根据题意,得l=≈2R.∵扇形的周长为16,∴l+2R=16,即4R=16,R=4,∴l=8,∴S=×4×8=16.故选A.
【点评】本题考查了扇形的面积公式S=(其中n为扇形的圆心角的度数,R为圆的半径)或S=lR,l为扇形的弧长,R为半径.同时考查了弧长公式.
5.D【解析】设这条弧所在的半径为xcm,则=2π×4,解得x=6.故选D.
【点评】此题主要考查了弧长公式以及圆的周长公式,根据弧长相等得出等式是解题的关键.
6.B【解析】∵等腰三角形的面积是10cm2,底边上的高线是5cm,∴底边长为4cm,∴圆锥底面圆的直径为4cm,∴侧面展开图的弧长为4πcm.故选B.
【点评】本题考查了圆锥的计算,重点是知道圆锥的底面周长等于圆锥的侧面展开扇形的弧长.
7.B【解析】设母线长为R,底面半径是3cm,则底面周长=6π,侧面积=3πR=12π,∴R=4cm.
故选B.
【点评】本题考查了圆锥的计算,利用了圆的周长公式和扇形面积公式求解.
8.C【解析】如答图,过点C作CD⊥OB,CE⊥OA.∵OB=OA,∠AOB=90°,∴△AOB是等腰直角三角形.∵OA是直径,∴∠ACO=90°,∴△AOC是等腰直角三角形.∵CE⊥OA,∴OE=AE,OC=AC,在Rt△OCE与Rt△ACE中,∵,∴Rt△OCE≌Rt△ACE.∵S扇形OEC=S扇形AEC,∴与弦OC围成的弓形的面积等于与弦AC所围成的弓形面积,同理可得,与弦OC围成的弓形的面积等于与弦BC所围成的弓形面积,∴S阴影=S△AOB=×1×1=cm2.故选C.
(第8题答图)
【点评】本题考查的是扇形面积的计算与等腰直角三角形的判定与性质,根据题意作出辅助线,构造出直角三角形得出S阴影=S△AOB是解答此题的关键.
9.D【解析】设圆锥的底面半径为1,则圆柱的底面半径,圆锥的高都为1,∴圆锥的母线长为=,∴圆柱的侧面积=2π×1×1=2π,圆锥的侧面积为×2π×=π,∴圆锥的侧面积与圆柱的侧面积之比为.故选D.
【点评】考查圆锥和圆柱侧面积的计算,熟记相应的公式是解决本题的关键.用到的知识点为:圆锥的底面半径,母线长,高组成以母线长为斜边的直角三角形.
10.B【解析】一个底面圆的半径为4m,高为3m,由勾股定理得,母线长为5,则它的底面周长为8π,侧面面积为×8π×5=20π;一个底面圆的半径为3m,高为4m,由勾股定理得,母线长为5,则它的底面周长为6π,侧面面积为×6π×5=15π.∵20π>15π,∴底面圆的半径大的侧面积大.故选B.
【点评】本题利用了勾股定理,圆的周长公式和扇形面积公式求解.
二.11.14.4°【解析】∵扇形的面积公式为S=LR,∴L=,∴L=4π.∵弧长公式为L=θR,∴θ=,∴θ=π=14.4°.
【点评】本题考查了扇形面积的计算和弧长的计算公式的运用.
12.π【解析】阴影部分的图形为扇形.扇形的圆心角大约是90度,所以它的面积约为=π.
【点评】一条弧和经过这条弧两端的两条半径所围成的图形叫扇形.扇形的面积公式为.
13.216°,96π【解析】圆锥的底面周长为2π?6=12πcm,扇形的面积为×10?12π=,解得n=216°.∵圆锥的表面积=圆锥的底面积+侧面积(扇形的面积),∴圆锥的表面积为36π+60π=96π.
【点评】本题考查了圆锥的计算,注意:正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆的周长是扇形的弧长.圆锥表面积=底面积+侧面积=π×底面半径2+底面周长×母线长÷2的应用.
14.2π,72°,18【解析】1)弧长l==2π;
(2)∵l=,∴圆心角的度数n==72°;
(3)∵l=,∴半径r==18.
【点评】本题主要考查了弧长的计算公式,是需要熟练掌握的内容.
15.6【解析】设圆柱的底面圆的半径为r,那么侧面积为2πr×10=120π,r=6cm.
故圆柱的底面圆的半径为6cm.
【点评】圆柱的计算要注意侧面积的计算公式为底面圆的周长×圆柱的高=圆柱的侧面积.
16.12【解析】设半径是r.∵一个扇形的弧长是8πcm,扇形的面积为48πcm2,∴48π=
×8π×r,∴r=12.
【点评】此题考查了扇形的面积公式.此题比较简单,解题的关键是熟记扇形的公式.
17.π【解析】∵∠AOB=60°,AB=3cm,∴三角形OAB是等边三角形,∴圆的半径是3厘米,
则劣弧AB的长为=π(cm).答:劣弧AB的长为πcm.
【点评】本题考查了弧长的计算,关键是先判断出三角形为等边三角形,再利用圆的弧长公式解答.
18.【解析】结合图形,得阴影部分的面积为=(cm2).
【点评】能够结合图形发现阴影部分的面积即为圆心角为40°,AB为半径的扇形的面积.
19.60【解析】设该扇形的圆心角的度数是n°.根据题意,得54π=,∴n=60.
∴该扇形的圆心角的度数是60°.
【点评】此题考查了扇形面积公式的应用.此题比较简单,难度不大,解题的关键是注意熟记扇形面积公式.
20.l=【解析】弧长的公式为l=.
【点评】本题考查了弧长的公式l=,是基础知识比较简单,要识记.
21.【解析】l===.
【点评】本题考查了弧长的计算公式,运用公式解题时,需注意公式中n的值在代入计算时不能带有度数.
22.12+2π【解析】由题意,得6π=,解得R=6,则l==2π,故扇形的周长为12+2π.
【点评】本题考查了扇形的面积计算及弧长的计算,解答本题的关键是熟练记忆扇形的面积公式及弧长的计算公式.
23.3【解析】设原弧长为,则扩大后的弧长是=3×,弧长与原弧长的比为3×:=3.
【点评】主要考查了弧长的计算.牢记弧长公式:c=.其中n是弧所对的圆心角的度数,r是半径.
24.【解析】根据题意,得S阴影部分=S扇形BAC﹣S半圆BC.∵S扇形BAC==,
S半圆BC=π(a)2=,∴S阴影部分=﹣=.
【点评】本题考查了扇形的面积公式:S=,其中n为扇形的圆心角的度数,R为圆的半径)或S=lR,l为扇形的弧长,R为半径.
25.10π;60°;6π;8,22.5°【解析】(1)S==10π;S=lR=10π,l=
2π.
(2)6π=,解得n=60,即圆心角为60°;S=lR=6π,l=2π.
(3)S=×2×6π=6π;S==6π,n=540°.
(4)4π=×π×R,解得R=8.
∴4π=,解得n=22.5,即圆心角为22.5°.
填表如下:
半径r 圆心角度数n 弧长l 扇形面积s
10 36° 2π 10π
6 60° 2π 6π
2 540° 6π 6π
8 22.5° π 4π
【点评】本题考查了扇形的面积公式S=,其中n为扇形的圆心角的度数,R为圆的半径)或S=lR,l为扇形的弧长,R为半径.
三.26.解:如答图,连接CD.
∵AB为半圆的直径,点C、D三等分半圆,
∴∠AOC=∠COD=∠BOD=×180°=60°,而OC=OD,
∴△OCD为等边三角形,
∴∠OCD=60°,
∴CD∥AB,
∴S△BCD=S△OCD,
∴S阴影=S扇形OCD==π(cm)2.
(第26题答图)
【点评】本题考查了扇形的面积公式:S=(n为扇形的圆心角的度数,R为圆的半径)以及弧与圆心角之间的关系以及等边三角形的性质,根据已知得出阴影部分的面积=S扇形OCD是解题关键.
27.解:连接OB,OC,如答图.
∵AB是圆O的切线,
∴∠ABO=90°.
在直角△ABO中,OB=2,OA=4,
∴∠OAB=30°,∠AOB=60°.
∵OA∥BC,
∴∠CBO=∠AOB=60°,且S阴影部分=S扇形△BOC,
∴△BOC是等边三角形,边长是2,
∴S阴影部分=S扇形△BOC==,即图中阴影部分的面积是.
(第27题答图)
【点评】本题主要考查了三角形的面积的计算,以及切线的性质,正确证明△BOC是等边三角形是解题的关键.
28.解:连接CO,OD,CD,如答图.
∵C,D是这个半圆的三等分点,
∴CD∥AB,∠COD=60°,
∴∠CAD的度数为30°.
∵OC=OD,∴△OCD是等边三角形,CD=OC=AB=6,
∴△OCD与△CDA是等底等高的三角形,
∴S阴影=S扇形OCD=π×62=6πcm2.
答:阴影部分的面积S是6πcm2.
(第28题答图)
【点评】本题主要考查了扇形面积公式的应用,关键是判断出△OCD与△CDA是等底等高的三角形,且△OCD是等边三角形,利用扇形的面积公式求解.
29.解:如答图.⊙O的半径为2,⊙C的半径为,点O在⊙C上,连OA,OB,OC.
∵OA=2,CA=CB=,即22=()2+()2,
∴OA2=CA2+CB2,
∴△OCA为直角三角形,
∴∠AOC=45°,
同理可得∠BOC=45°,
∴∠AOB=90°,
∴AB为⊙C的直径.
∴S阴影部分=S半圆AB﹣S弓形AB=S半圆AB﹣(S扇形OAB﹣S△OAB)=π×()2﹣+×2×2=2.
(第29题答图)
【点评】本题考查了扇形的面积公式:S=,其中n为扇形的圆心角的度数,R为圆的半径)或S=lR,l为扇形的弧长,R为半径.也考查了勾股定理以及90度的圆周角所对的弦为直径.
30.解:由题图可知,将△OAC顺时针旋转90°后可与△ODB重合,
∴S△OAC=S△OBD.
因此S阴影=S扇形OAB+S△OBD﹣S△OAC﹣S扇形OCD=S扇形OAB﹣S扇形OCD=π×(9﹣1)=2π cm2.
即阴影部分的面积是2π cm2.
【点评】本题中阴影部分的面积可以看作是扇形AOB与扇形COD的面积差,求不规则的图形的面积,可以转化为几个规则图形的面积的和或差来求.
31.解:如答图,连接OC,OD.
∵C,D是以AB为直径的半圆上的三等分点,
∴∠COD=60°.
∵△ACD的面积等于△OCD的面积,
∴都加上CD之间弓形的面积得出S阴影=S扇形OCD,
∴=(提示:连接CO,DO,S阴影=S扇形COD).
(第31题答图)
【点评】本题的关键是仔细观察图形,从图中看出S阴影=S扇形COD.
32.解:由题图知,底面直径为5米,所以底面半径为2.5米,
∴圆锥的母线长=≈2.77(米),
∴圆锥的侧面积=×5π×2.77≈21.74(平方米);
圆柱的侧面积=5π×1.8≈28.26(平方米).
∴故需要蓬布21.76+28.26≈50.0(平方米).
【点评】本题利用了勾股定理,圆面积公式,扇形的面积公式,矩形的面积公式求解.
一.选择题(共10小题)
1.下列各结论,正确的为( )
A.圆心角相等的两个扇形相同
B.圆心角相等的两个扇形的面积相等
C.两个面积相等的扇形的圆心角相等
D.同圆或等圆中面积相等的两个扇形的圆心角相等
2.若一个扇形的面积是相应圆的面积的,则它的圆心角为( )
A.150° B.120° C.90° D.60°
3.如果圆锥的高为3cm,母线长为5cm,则圆锥的侧面积是( )
A.16πcm2 B.20πcm2 C.28πcm2 D.36πcm2
4.扇形的周长为16,圆心角为120°,则扇形的面积为( )
A.16 B.32 C.64 D.16π
5.一条圆弧所对的圆心角等于240°,它的长度等于半径为4cm的圆的周长,则这条弧所在的半径为( )
A.3cm B.4cm C.5cm D.6cm
6.圆锥的轴截面是一个等腰三角形,它的面积是10cm2,底边上的高线是5cm,则圆锥的侧面展开图的弧长等于( )
A.8π cm B.4π cm C.8 cm D.4 cm
7.若圆锥的侧面积为12π cm2,它的底面半径为3cm,则此圆锥的母线长为( )
A.4π cm B.4 cm C.2π cm D.2 cm
8.如图,半径为1cm,圆心角为90°的扇形OAB中,分别以OA,OB为直径作半圆,则图中阴影部分的面积为( )
(第8题图)
A.πcm2 B.πcm2 C.cm2 D.cm2
9.一个圆锥和一个圆柱的底面半径相等,且它们的高都等于它们的底面半径,那么它们的侧面积之比为( )
A. B. C. D.
10.两个圆锥,其中一个底面圆的半径为4m,高为3m,另一个底面圆的半径为3m,高为4m,那么这两个圆锥的侧面积( )
A.相等 B.底面圆的半径大的侧面积大
C.底面圆的半径小的侧面积大 D.不能确定
二.填空题(共15小题)
11.若一扇形的面积为100πcm2,此扇形所在圆的半径为50cm,则扇形的圆心角的度数
为 °.
12.如图,阴影部分的图形叫 ,若圆的半径是1,估计它的面积约为 (结果用π表示)
(第12题图)
13.圆锥的底面半径为6cm,母线长为10cm,则它的侧面展开图的圆心角等于 ,表面积为 ;
14.填表:
半径r 圆心角的度数n 弧长l
10 36°
5 2π
120° 12π
(圆周率用π表示即可)
15.一个圆柱的侧面积为120πcm2,高为10cm,则它的底面圆的半径为 .
16.若一个扇形的弧长是8πcm,扇形的面积为48πcm2,则半径是 .
17.如图,在⊙O中,∠AOB=60°,AB=3cm,则劣弧AB的长为 cm.
(第17题图)
18.如图,将一个半径为4cm的半圆绕直径AB的一个端点A旋转40°,那么图中阴影部分的面积为 cm2.
(第18题图)
19.若面积为54πcm2的扇形的半径为18cm,则该扇形的圆心角的度数是 .
20.弧长的计算:如果弧长为l,圆心角的度数为n,圆的半径为r,那么弧长l= .
21.一条弧所对的圆心角是90°,半径是R,则这条弧长为 .
22.扇形的圆心角的度数为60°,面积为6π,则扇形的周长为 .
23.如果圆弧的度数扩大2倍,半径为原来的,则弧长与原弧长的比为 .
24.如图,正方形ABCD边长为a,那么阴影部分的面积S是 .
(第24题图)
25.填表:
半径r 圆心角的度数n 弧长l 扇形面积s
10 36°
6 6π
2 6π
π 4π
三.解答题(共7小题)
26.如图,半圆的半径为2cm,点C,D三等分半圆,求阴影部分的面积.
(第26题图)
27.如图,A是半径为2的⊙O外一点,OA=4,AB是⊙O的切线,B为切点,弦BC∥OA,连接AC,求阴影部分的面积.
(第27题图)
28.已知:如图,半圆O的直径AB=12cm,C,D是这个半圆的三等分点.求∠CAD的度数及弦AC,AD和围成的图形(图中阴影部分)的面积S.
(第28题图)
29.如图所示,一个半径为的圆过一个半径为2的圆的圆心,则图中阴影部分的面积是多少?
(第29题图)
30.圆心角都是90°的扇形OAB与扇形OCD按如图所示的方式叠放在一起,连结AC,BD.若AO=3cm,OC=1cm,求阴影部分的面积.
(第30题图)
31.如图所示,C,D是以AB为直径的半圆上的三等分点,半径为R,求图中阴影部分的面积.
(第31题图)
32.牧民居住的蒙古包的形状是一个圆柱与圆锥的组合体,尺寸如图所示,请你算出要搭建这样一个蒙古包至少需要多少平方米的蓬布?(π取3.14,结果保留一位小数)
(第32题图)
参考答案
一.1.D【解析】因为不是在同一个圆中的扇形的面积和圆心角都无法比较,故可以排除A,B,C, 而对于同一个圆中,扇形的面积为s=lα2,其中l为圆的半径,α为圆心角.故选D.
【点评】本题涉及圆和圆心角的相应知识,难度一般.
2.C【解析】设圆的面积=πr2,则扇形的面积==,解得n=90°.故选C.
【点评】本题主要是利用扇形的面积是相应圆的面积的关系,列出等式,求得圆心角的度数.
3.B【解析】圆锥的高为3cm,母线长为5cm,由勾股定理,得底面半径为4cm,底面周长为8πcm,侧面展开图的面积为×8π×5=20πcm2.故选B.
【点评】本题利用了勾股定理,圆的周长公式和扇形的面积公式求解.
4.A【解析】根据题意,得l=≈2R.∵扇形的周长为16,∴l+2R=16,即4R=16,R=4,∴l=8,∴S=×4×8=16.故选A.
【点评】本题考查了扇形的面积公式S=(其中n为扇形的圆心角的度数,R为圆的半径)或S=lR,l为扇形的弧长,R为半径.同时考查了弧长公式.
5.D【解析】设这条弧所在的半径为xcm,则=2π×4,解得x=6.故选D.
【点评】此题主要考查了弧长公式以及圆的周长公式,根据弧长相等得出等式是解题的关键.
6.B【解析】∵等腰三角形的面积是10cm2,底边上的高线是5cm,∴底边长为4cm,∴圆锥底面圆的直径为4cm,∴侧面展开图的弧长为4πcm.故选B.
【点评】本题考查了圆锥的计算,重点是知道圆锥的底面周长等于圆锥的侧面展开扇形的弧长.
7.B【解析】设母线长为R,底面半径是3cm,则底面周长=6π,侧面积=3πR=12π,∴R=4cm.
故选B.
【点评】本题考查了圆锥的计算,利用了圆的周长公式和扇形面积公式求解.
8.C【解析】如答图,过点C作CD⊥OB,CE⊥OA.∵OB=OA,∠AOB=90°,∴△AOB是等腰直角三角形.∵OA是直径,∴∠ACO=90°,∴△AOC是等腰直角三角形.∵CE⊥OA,∴OE=AE,OC=AC,在Rt△OCE与Rt△ACE中,∵,∴Rt△OCE≌Rt△ACE.∵S扇形OEC=S扇形AEC,∴与弦OC围成的弓形的面积等于与弦AC所围成的弓形面积,同理可得,与弦OC围成的弓形的面积等于与弦BC所围成的弓形面积,∴S阴影=S△AOB=×1×1=cm2.故选C.
(第8题答图)
【点评】本题考查的是扇形面积的计算与等腰直角三角形的判定与性质,根据题意作出辅助线,构造出直角三角形得出S阴影=S△AOB是解答此题的关键.
9.D【解析】设圆锥的底面半径为1,则圆柱的底面半径,圆锥的高都为1,∴圆锥的母线长为=,∴圆柱的侧面积=2π×1×1=2π,圆锥的侧面积为×2π×=π,∴圆锥的侧面积与圆柱的侧面积之比为.故选D.
【点评】考查圆锥和圆柱侧面积的计算,熟记相应的公式是解决本题的关键.用到的知识点为:圆锥的底面半径,母线长,高组成以母线长为斜边的直角三角形.
10.B【解析】一个底面圆的半径为4m,高为3m,由勾股定理得,母线长为5,则它的底面周长为8π,侧面面积为×8π×5=20π;一个底面圆的半径为3m,高为4m,由勾股定理得,母线长为5,则它的底面周长为6π,侧面面积为×6π×5=15π.∵20π>15π,∴底面圆的半径大的侧面积大.故选B.
【点评】本题利用了勾股定理,圆的周长公式和扇形面积公式求解.
二.11.14.4°【解析】∵扇形的面积公式为S=LR,∴L=,∴L=4π.∵弧长公式为L=θR,∴θ=,∴θ=π=14.4°.
【点评】本题考查了扇形面积的计算和弧长的计算公式的运用.
12.π【解析】阴影部分的图形为扇形.扇形的圆心角大约是90度,所以它的面积约为=π.
【点评】一条弧和经过这条弧两端的两条半径所围成的图形叫扇形.扇形的面积公式为.
13.216°,96π【解析】圆锥的底面周长为2π?6=12πcm,扇形的面积为×10?12π=,解得n=216°.∵圆锥的表面积=圆锥的底面积+侧面积(扇形的面积),∴圆锥的表面积为36π+60π=96π.
【点评】本题考查了圆锥的计算,注意:正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆的周长是扇形的弧长.圆锥表面积=底面积+侧面积=π×底面半径2+底面周长×母线长÷2的应用.
14.2π,72°,18【解析】1)弧长l==2π;
(2)∵l=,∴圆心角的度数n==72°;
(3)∵l=,∴半径r==18.
【点评】本题主要考查了弧长的计算公式,是需要熟练掌握的内容.
15.6【解析】设圆柱的底面圆的半径为r,那么侧面积为2πr×10=120π,r=6cm.
故圆柱的底面圆的半径为6cm.
【点评】圆柱的计算要注意侧面积的计算公式为底面圆的周长×圆柱的高=圆柱的侧面积.
16.12【解析】设半径是r.∵一个扇形的弧长是8πcm,扇形的面积为48πcm2,∴48π=
×8π×r,∴r=12.
【点评】此题考查了扇形的面积公式.此题比较简单,解题的关键是熟记扇形的公式.
17.π【解析】∵∠AOB=60°,AB=3cm,∴三角形OAB是等边三角形,∴圆的半径是3厘米,
则劣弧AB的长为=π(cm).答:劣弧AB的长为πcm.
【点评】本题考查了弧长的计算,关键是先判断出三角形为等边三角形,再利用圆的弧长公式解答.
18.【解析】结合图形,得阴影部分的面积为=(cm2).
【点评】能够结合图形发现阴影部分的面积即为圆心角为40°,AB为半径的扇形的面积.
19.60【解析】设该扇形的圆心角的度数是n°.根据题意,得54π=,∴n=60.
∴该扇形的圆心角的度数是60°.
【点评】此题考查了扇形面积公式的应用.此题比较简单,难度不大,解题的关键是注意熟记扇形面积公式.
20.l=【解析】弧长的公式为l=.
【点评】本题考查了弧长的公式l=,是基础知识比较简单,要识记.
21.【解析】l===.
【点评】本题考查了弧长的计算公式,运用公式解题时,需注意公式中n的值在代入计算时不能带有度数.
22.12+2π【解析】由题意,得6π=,解得R=6,则l==2π,故扇形的周长为12+2π.
【点评】本题考查了扇形的面积计算及弧长的计算,解答本题的关键是熟练记忆扇形的面积公式及弧长的计算公式.
23.3【解析】设原弧长为,则扩大后的弧长是=3×,弧长与原弧长的比为3×:=3.
【点评】主要考查了弧长的计算.牢记弧长公式:c=.其中n是弧所对的圆心角的度数,r是半径.
24.【解析】根据题意,得S阴影部分=S扇形BAC﹣S半圆BC.∵S扇形BAC==,
S半圆BC=π(a)2=,∴S阴影部分=﹣=.
【点评】本题考查了扇形的面积公式:S=,其中n为扇形的圆心角的度数,R为圆的半径)或S=lR,l为扇形的弧长,R为半径.
25.10π;60°;6π;8,22.5°【解析】(1)S==10π;S=lR=10π,l=
2π.
(2)6π=,解得n=60,即圆心角为60°;S=lR=6π,l=2π.
(3)S=×2×6π=6π;S==6π,n=540°.
(4)4π=×π×R,解得R=8.
∴4π=,解得n=22.5,即圆心角为22.5°.
填表如下:
半径r 圆心角度数n 弧长l 扇形面积s
10 36° 2π 10π
6 60° 2π 6π
2 540° 6π 6π
8 22.5° π 4π
【点评】本题考查了扇形的面积公式S=,其中n为扇形的圆心角的度数,R为圆的半径)或S=lR,l为扇形的弧长,R为半径.
三.26.解:如答图,连接CD.
∵AB为半圆的直径,点C、D三等分半圆,
∴∠AOC=∠COD=∠BOD=×180°=60°,而OC=OD,
∴△OCD为等边三角形,
∴∠OCD=60°,
∴CD∥AB,
∴S△BCD=S△OCD,
∴S阴影=S扇形OCD==π(cm)2.
(第26题答图)
【点评】本题考查了扇形的面积公式:S=(n为扇形的圆心角的度数,R为圆的半径)以及弧与圆心角之间的关系以及等边三角形的性质,根据已知得出阴影部分的面积=S扇形OCD是解题关键.
27.解:连接OB,OC,如答图.
∵AB是圆O的切线,
∴∠ABO=90°.
在直角△ABO中,OB=2,OA=4,
∴∠OAB=30°,∠AOB=60°.
∵OA∥BC,
∴∠CBO=∠AOB=60°,且S阴影部分=S扇形△BOC,
∴△BOC是等边三角形,边长是2,
∴S阴影部分=S扇形△BOC==,即图中阴影部分的面积是.
(第27题答图)
【点评】本题主要考查了三角形的面积的计算,以及切线的性质,正确证明△BOC是等边三角形是解题的关键.
28.解:连接CO,OD,CD,如答图.
∵C,D是这个半圆的三等分点,
∴CD∥AB,∠COD=60°,
∴∠CAD的度数为30°.
∵OC=OD,∴△OCD是等边三角形,CD=OC=AB=6,
∴△OCD与△CDA是等底等高的三角形,
∴S阴影=S扇形OCD=π×62=6πcm2.
答:阴影部分的面积S是6πcm2.
(第28题答图)
【点评】本题主要考查了扇形面积公式的应用,关键是判断出△OCD与△CDA是等底等高的三角形,且△OCD是等边三角形,利用扇形的面积公式求解.
29.解:如答图.⊙O的半径为2,⊙C的半径为,点O在⊙C上,连OA,OB,OC.
∵OA=2,CA=CB=,即22=()2+()2,
∴OA2=CA2+CB2,
∴△OCA为直角三角形,
∴∠AOC=45°,
同理可得∠BOC=45°,
∴∠AOB=90°,
∴AB为⊙C的直径.
∴S阴影部分=S半圆AB﹣S弓形AB=S半圆AB﹣(S扇形OAB﹣S△OAB)=π×()2﹣+×2×2=2.
(第29题答图)
【点评】本题考查了扇形的面积公式:S=,其中n为扇形的圆心角的度数,R为圆的半径)或S=lR,l为扇形的弧长,R为半径.也考查了勾股定理以及90度的圆周角所对的弦为直径.
30.解:由题图可知,将△OAC顺时针旋转90°后可与△ODB重合,
∴S△OAC=S△OBD.
因此S阴影=S扇形OAB+S△OBD﹣S△OAC﹣S扇形OCD=S扇形OAB﹣S扇形OCD=π×(9﹣1)=2π cm2.
即阴影部分的面积是2π cm2.
【点评】本题中阴影部分的面积可以看作是扇形AOB与扇形COD的面积差,求不规则的图形的面积,可以转化为几个规则图形的面积的和或差来求.
31.解:如答图,连接OC,OD.
∵C,D是以AB为直径的半圆上的三等分点,
∴∠COD=60°.
∵△ACD的面积等于△OCD的面积,
∴都加上CD之间弓形的面积得出S阴影=S扇形OCD,
∴=(提示:连接CO,DO,S阴影=S扇形COD).
(第31题答图)
【点评】本题的关键是仔细观察图形,从图中看出S阴影=S扇形COD.
32.解:由题图知,底面直径为5米,所以底面半径为2.5米,
∴圆锥的母线长=≈2.77(米),
∴圆锥的侧面积=×5π×2.77≈21.74(平方米);
圆柱的侧面积=5π×1.8≈28.26(平方米).
∴故需要蓬布21.76+28.26≈50.0(平方米).
【点评】本题利用了勾股定理,圆面积公式,扇形的面积公式,矩形的面积公式求解.
