沪科版2019_2020学年九年级数学下册期中达标检测卷含答案
文档属性
| 名称 | 沪科版2019_2020学年九年级数学下册期中达标检测卷含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 159.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-03 21:49:34 | ||
图片预览


文档简介
期中达标检测卷
一、选择题(每小题4分,共32分)在每小题给出的四个选项中, 只有一项是符合题目要求的.
1. 已知⊙O的半径是6cm,点O到同一平面内直线l的距离为5cm,则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.无法判断
2.如图,点A、B、C在⊙O上,∠ABC=50°,则∠AOC的度数为( )
A.120° B.100° C.50° D.25°
3.如图在△ABC中,∠B=90°, ∠A=30°,AC=4cm,将△ABC绕顶点C顺时针方向旋转至△的位置,且A、C、B′三点在同一条直线上,则点A所经过的最短路线的长为( )
A. B. 8cm C. D.
4.如图,的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为( )
A.126° B. 54° C. 30° D. 36°
5.如图,已知⊙O的半径为1,AB与⊙O相切于点A,OB与⊙O交
于点C,CD⊥OA,垂足为D,则sin∠AOB的值等于( )
A.CD B.OA C.OD D.AB
6.用半径为3cm,圆心角是120°的扇形围成一个圆锥的侧面,则
该圆锥的底面半径为( )
A. 2πcm B. 1cm C. πcm D. 1.5cm
7. 如图,CD是⊙O的直径,弦AB⊥CD于点G,直线EF与
⊙O相切于点D,则下列结论不一定正确的是( )
A. AG=BG B.AB//EF
C.AD//BC D.∠ABC=∠ADC
8. 若正方形的边长为6,则其外接圆的半径与内切圆的半径的大小分别为( )
A.6, B.,3 C.6,3 D.,
二、填空题(每小题4分,共24分)请把答案填写在题中的横线上.
9.一条弦把圆分成2:3的两部分,那么这条弦所对的圆周角的度数为_________.
10.已知圆锥的母线长为5cm,底面直径为4cm,则侧面展开图的圆心角的度数是_________.
11.Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以点C为圆心,r为半径作圆,若圆C与直线AB相切,则r的值为_________.
12.钟表的轴心到分针针尖的长为5cm,那么经过40分钟,分针针尖转过的弧长是_________cm.
13.如图,AB是⊙O的直径,C、D是圆上的两点(不与A、B重合),已知BC=2,tan∠ADC=1,则AB=__________.
14. 如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E.B,E是半圆弧的三等分点,弧BE的长为,则图中阴影部分的面积为 .
三、 解答题(本题共5小题,共44分)
15.(7分)如图所示,某窗户由矩形和弓形组成.已知弓形的跨度AB=3m,弓形的高EF=1m.现计划安装玻璃,请帮工程师求出所在圆O的半径.
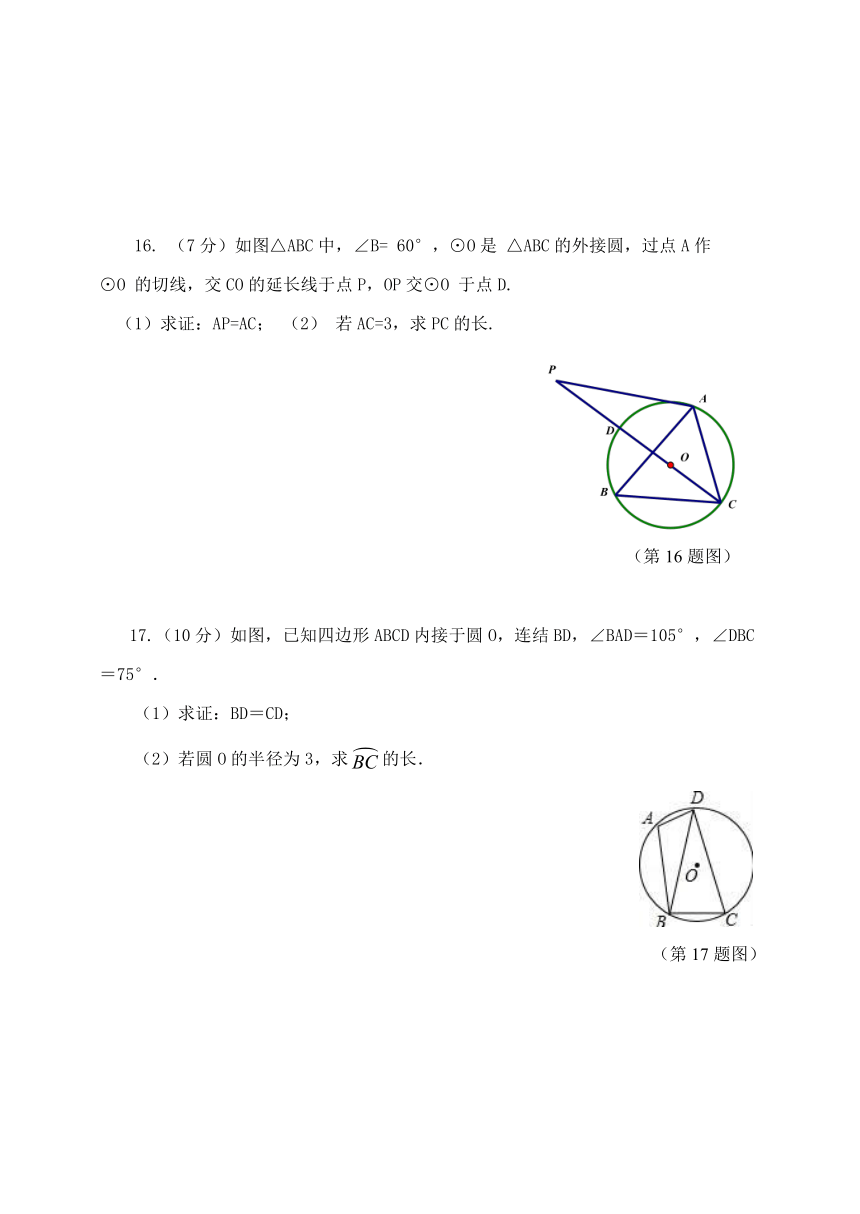
16. (7分)如图△ABC中,∠B= 60°,⊙O是 △ABC的外接圆,过点A作
⊙O 的切线,交CO的延长线于点P,OP交⊙O 于点D.
(1)求证:AP=AC; (2) 若AC=3,求PC的长.
17.(10分)如图,已知四边形ABCD内接于圆O,连结BD,∠BAD=105°,∠DBC=75°.
(1)求证:BD=CD;
(2)若圆O的半径为3,求的长.
18.(10分)如图,AB是⊙O的直径,AC是⊙O的弦,过点B作⊙O的切线DE,与AC的延长线交于点D,作AE⊥AC交DE于点E.
(1)求证:∠BAD=∠E;
(2)若⊙O的半径为5,AC=8,求BE的长.
19.(10分)如图,BC是⊙O的直径, A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D,取CD的中点E,AE的延长线与BC的延长线交于点P.
(1)求证:AP是⊙O的切线;
(2)若OC=CP,AB=6,求CD的长.
参考答案
一、1.A. 2.B. 3.D 4.D 5.A 6.B 7.C 8.B
二、9.72°或108° 10. 144° 11.2.4 12. 13. 14. .
三、15. 解:设⊙O的半径为r,则OF=r-1.
由垂径定理,得BF=AB=1.5,OF⊥AB.
由OF2 +BF2= OB2,得(r-1)2+1.52 = r 2,
解得r =.
答:所在圆O的半径为.
16.(1)连结OA.∵,AP为切线,∴OA ⊥ AP,∠AOC=120°.
又∵OA=OC, ∴∠ACP=30°,∠P=30°, ∴AP=AC.
(2)先求OC=,再证明△OAC∽△APC , =,得PC=.
17. (1)证明:∵四边形ABCD内接于圆O,∴∠DCB+∠BAD=180°.
∵∠BAD=105°,∴∠DCB=180°-105°=75°.
∵∠DBC=75°,∴∠DCB=∠DBC=75°.∴BD=CD.
(2)解:∵∠DCB=∠DBC=75°,∴∠BDC=30°.
由圆周角定理,得的度数为60°,故===π.
答:的长为π.
18.证明:(1)∵⊙O与DE相切于点B,AB为⊙O的直径,
∴∠ABE=90°.∴∠BAE+∠E=90°.
又∵∠DAE=90°,∴∠BAD+∠BAE=90°.
∴∠BAD=∠E.
(2)解:如图,连接BC.
∵AB为⊙O直径,∴∠ACB=90°. (第18题答图)
∵AC=8,AB=2×5=10,
∴BC==6.又∵∠BCA=∠ABE=90°,∠BAD=∠E,
∴△ABC∽△EAB.
∴=. ∴=,∴BE=.
19.解:(1)证明:连接AO,AC.
∵BC是⊙O的直径,∴∠BAC=90°,∴∠CAD=90°.
∵E是CD的中点,∴CE=AE.
在等腰△EAC中,∠ECA=∠EAC.
∵OA=OC,∴∠OAC= ∠OCA.
∵CD是⊙O的切线,∴CD⊥OC,
∴∠ECA+∠OAC = 90°,
∴∠EAC+∠OAC = 90°.
∴OA⊥AP,∴AP是⊙O的切线.
(2)由(1)知,OA⊥AP.
在Rt△OAP中,∵∠OAP=90°, OC=CP=OA,即OP=2OA,
∴,∴,∴,
∴.
又∵在Rt△DAC中,∠CAD = 90°, ∠ACD = 90°-∠ACO= 30°,
∴.
(第3题图)
A
O
B
C
(第2题图)
(第4题图)
B
C
A
O
D
(第5题图)
E
O
F
C
D
B
G
A
(第7题图)
(第13题图)
(第14题图)
(第15题图)
(第16题图)
(第17题图)
(第18题图)
(第19题图)
PAGE
一、选择题(每小题4分,共32分)在每小题给出的四个选项中, 只有一项是符合题目要求的.
1. 已知⊙O的半径是6cm,点O到同一平面内直线l的距离为5cm,则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.无法判断
2.如图,点A、B、C在⊙O上,∠ABC=50°,则∠AOC的度数为( )
A.120° B.100° C.50° D.25°
3.如图在△ABC中,∠B=90°, ∠A=30°,AC=4cm,将△ABC绕顶点C顺时针方向旋转至△的位置,且A、C、B′三点在同一条直线上,则点A所经过的最短路线的长为( )
A. B. 8cm C. D.
4.如图,的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为( )
A.126° B. 54° C. 30° D. 36°
5.如图,已知⊙O的半径为1,AB与⊙O相切于点A,OB与⊙O交
于点C,CD⊥OA,垂足为D,则sin∠AOB的值等于( )
A.CD B.OA C.OD D.AB
6.用半径为3cm,圆心角是120°的扇形围成一个圆锥的侧面,则
该圆锥的底面半径为( )
A. 2πcm B. 1cm C. πcm D. 1.5cm
7. 如图,CD是⊙O的直径,弦AB⊥CD于点G,直线EF与
⊙O相切于点D,则下列结论不一定正确的是( )
A. AG=BG B.AB//EF
C.AD//BC D.∠ABC=∠ADC
8. 若正方形的边长为6,则其外接圆的半径与内切圆的半径的大小分别为( )
A.6, B.,3 C.6,3 D.,
二、填空题(每小题4分,共24分)请把答案填写在题中的横线上.
9.一条弦把圆分成2:3的两部分,那么这条弦所对的圆周角的度数为_________.
10.已知圆锥的母线长为5cm,底面直径为4cm,则侧面展开图的圆心角的度数是_________.
11.Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以点C为圆心,r为半径作圆,若圆C与直线AB相切,则r的值为_________.
12.钟表的轴心到分针针尖的长为5cm,那么经过40分钟,分针针尖转过的弧长是_________cm.
13.如图,AB是⊙O的直径,C、D是圆上的两点(不与A、B重合),已知BC=2,tan∠ADC=1,则AB=__________.
14. 如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E.B,E是半圆弧的三等分点,弧BE的长为,则图中阴影部分的面积为 .
三、 解答题(本题共5小题,共44分)
15.(7分)如图所示,某窗户由矩形和弓形组成.已知弓形的跨度AB=3m,弓形的高EF=1m.现计划安装玻璃,请帮工程师求出所在圆O的半径.
16. (7分)如图△ABC中,∠B= 60°,⊙O是 △ABC的外接圆,过点A作
⊙O 的切线,交CO的延长线于点P,OP交⊙O 于点D.
(1)求证:AP=AC; (2) 若AC=3,求PC的长.
17.(10分)如图,已知四边形ABCD内接于圆O,连结BD,∠BAD=105°,∠DBC=75°.
(1)求证:BD=CD;
(2)若圆O的半径为3,求的长.
18.(10分)如图,AB是⊙O的直径,AC是⊙O的弦,过点B作⊙O的切线DE,与AC的延长线交于点D,作AE⊥AC交DE于点E.
(1)求证:∠BAD=∠E;
(2)若⊙O的半径为5,AC=8,求BE的长.
19.(10分)如图,BC是⊙O的直径, A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D,取CD的中点E,AE的延长线与BC的延长线交于点P.
(1)求证:AP是⊙O的切线;
(2)若OC=CP,AB=6,求CD的长.
参考答案
一、1.A. 2.B. 3.D 4.D 5.A 6.B 7.C 8.B
二、9.72°或108° 10. 144° 11.2.4 12. 13. 14. .
三、15. 解:设⊙O的半径为r,则OF=r-1.
由垂径定理,得BF=AB=1.5,OF⊥AB.
由OF2 +BF2= OB2,得(r-1)2+1.52 = r 2,
解得r =.
答:所在圆O的半径为.
16.(1)连结OA.∵,AP为切线,∴OA ⊥ AP,∠AOC=120°.
又∵OA=OC, ∴∠ACP=30°,∠P=30°, ∴AP=AC.
(2)先求OC=,再证明△OAC∽△APC , =,得PC=.
17. (1)证明:∵四边形ABCD内接于圆O,∴∠DCB+∠BAD=180°.
∵∠BAD=105°,∴∠DCB=180°-105°=75°.
∵∠DBC=75°,∴∠DCB=∠DBC=75°.∴BD=CD.
(2)解:∵∠DCB=∠DBC=75°,∴∠BDC=30°.
由圆周角定理,得的度数为60°,故===π.
答:的长为π.
18.证明:(1)∵⊙O与DE相切于点B,AB为⊙O的直径,
∴∠ABE=90°.∴∠BAE+∠E=90°.
又∵∠DAE=90°,∴∠BAD+∠BAE=90°.
∴∠BAD=∠E.
(2)解:如图,连接BC.
∵AB为⊙O直径,∴∠ACB=90°. (第18题答图)
∵AC=8,AB=2×5=10,
∴BC==6.又∵∠BCA=∠ABE=90°,∠BAD=∠E,
∴△ABC∽△EAB.
∴=. ∴=,∴BE=.
19.解:(1)证明:连接AO,AC.
∵BC是⊙O的直径,∴∠BAC=90°,∴∠CAD=90°.
∵E是CD的中点,∴CE=AE.
在等腰△EAC中,∠ECA=∠EAC.
∵OA=OC,∴∠OAC= ∠OCA.
∵CD是⊙O的切线,∴CD⊥OC,
∴∠ECA+∠OAC = 90°,
∴∠EAC+∠OAC = 90°.
∴OA⊥AP,∴AP是⊙O的切线.
(2)由(1)知,OA⊥AP.
在Rt△OAP中,∵∠OAP=90°, OC=CP=OA,即OP=2OA,
∴,∴,∴,
∴.
又∵在Rt△DAC中,∠CAD = 90°, ∠ACD = 90°-∠ACO= 30°,
∴.
(第3题图)
A
O
B
C
(第2题图)
(第4题图)
B
C
A
O
D
(第5题图)
E
O
F
C
D
B
G
A
(第7题图)
(第13题图)
(第14题图)
(第15题图)
(第16题图)
(第17题图)
(第18题图)
(第19题图)
PAGE
同课章节目录
