高中数学苏教版选修2-2第一章 1.4导数在实际生活的应用课件(共25张PPT)
文档属性
| 名称 | 高中数学苏教版选修2-2第一章 1.4导数在实际生活的应用课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-05 11:26:35 | ||
图片预览







文档简介
(共25张PPT)
导数在实际生活中的应用
苏教版教科书选修2-2《数学》
新课引入
导数在实际生活中有着广泛的应用,利用导数求最值的方法,可以解决实际生活中的某些最值问题.
1.几何方面的应用
2.物理方面的应用
3.经济学方面的应用
(如:面积、体积等最值问题)
(如:利润最大化问题等)
(如:功、功率等最值问题)
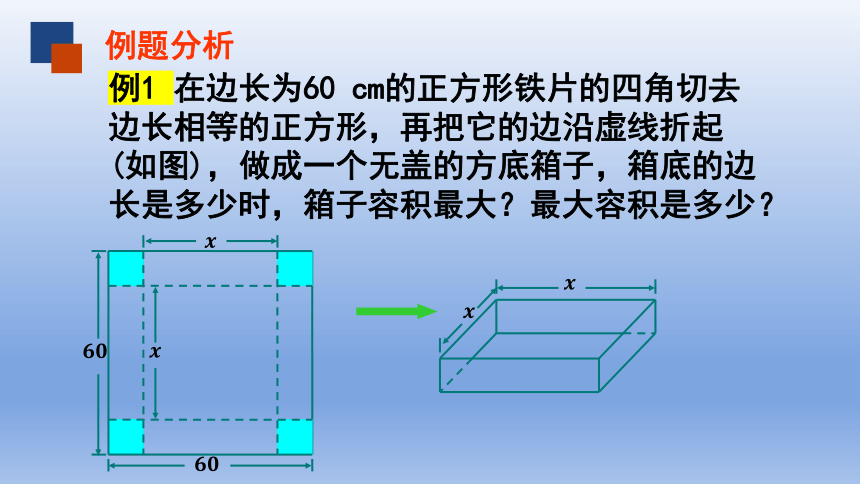
例1 在边长为60 cm的正方形铁片的四角切去边长相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱子容积最大?最大容积是多少?
例题分析
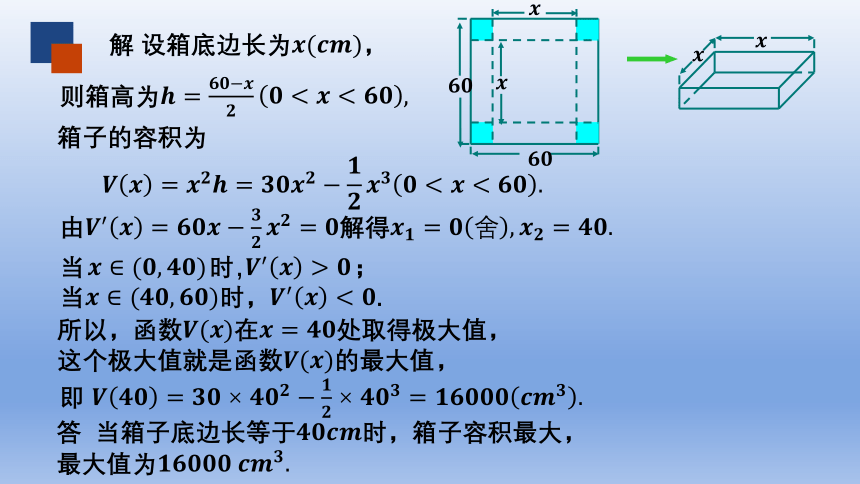
解 设箱底边长为,
则箱高为
箱子的容积为
由解得
当时,;当时,.
所以,函数在处取得极大值,
这个极大值就是函数的最大值,
即
答 当箱子底边长等于时,箱子容积最大,
最大值为
1.应用题解题基本步骤
解题回顾
2.本题利用了导数法求解容积最大问题
3.对于开区间内,如果函数只有一个极值,那么这个极值也是最值.
(2)建立数学模型;
(3)解答数学问题;
(4)检验并回答实际问题.
(1)仔细审题,明确题意;
例2 某种圆柱形饮料罐的容积一定,如何确定它的高与底半径,才能使它的用料最省?
解 设圆柱的高为,底半径为,
则表面积S=2
又圆柱体积(定值),则,故
由,解得
此时,,即
当时,;当时,
所以 ,当时,取得极小值,且是最小值.
答 当罐高与罐底的直径相等时,用料最省.
1.对于一个实际生活问题,我们需要将其转化为
数学问题,会用图形语言和数学符号语言表达问题.
解题回顾
2.出现两个或两个以上变量时,需要明确哪个字母是自变量,然后将其它变量用这个自变量表示,从而问题就转化成了一个单变量函数问题,我们再用导数法求这个函数的最值.
3.最后下结论时,要切合题目要求,准确回答.
练习
(1)求内接于半径为R的圆的矩形面积的最大值.
(2)求内接于半径为R的球的圆柱体积的最大值.
(1)求内接于半径为R的圆的矩形面积的最大值.
解 设矩形的一边长为,则另一边长为,
故矩形的面积为
令,对求导可得,.
令,可得.
当时,;当时,.
所以,当时,取得极大值,且为最大值,
此时,矩形面积取得最大值为
答 矩形面积的最大值为
(2)求内接于半径为R的球的圆柱体积的最大值.
解 设球内接圆柱的高为,圆柱底面半径为,
则
求导数,得.
当时,;当时,.
所以,当时,取得极大值,且为最大值,
此时,最大值为
答 圆柱的最大值为
故圆柱的体积为
1.导数在实际生活中的应用主要是解决有关最大(小)值问题;
2.解题时,先仔细审题,准确理解题意,将实际问题数学化,建立目标函数,然后用导数法求目标函数的最值,最后回到实际问题.
例3 在如图所示的电路中,已知电源的内阻为,电动势为.当外电阻为多大时,才能使电功率最大?最大电功率是多少?
解 电功率,其中为电流强度,
则.
例题解析
R
由,解得.
当时,;当R>时,
因此,当时,取得极大值,且是最大值,最大值为.
答 当外电阻等于内电阻时,电功率最大,最大电功率是
解题回顾
1.本题求解电功率的最大值问题用了导数法,
可见数学是物理研究的工具和手段.
2.解题中,出现多个字母时,要认清哪个是变量,
哪个是常量.
例4 强度分别为的两个点光源间的距离为,试问:在连结两光源的线段上,何处照度最小?试时回答上述问题.(照度与光的强度成正比,与光源距离的平方成反比)
解 如图,设点在线段上,且距光源为,则距光源为
点受光源的照度为,即;
点受光源的照度为,即,其中为比例常数.
从而,点的总照度为(0<<3).
由
解得 .
当<<时,<0;当<<时,>0.
因此,时取得极小值,且是最小值.
答 在连结两光源的线段上,距光源为处的照度最小.
我们特别要注意,
建立正确的目标函数的前提是准确理解题意.
例5 在经济学中,生产单位产品的成本称为成本函数,记为,出售单位产品的收益称为收益函数,记为, 称为利润函数,记为.
(1)如果,
那么生产多少单位产品时,边际成本最低?
(2)如果,产品的单价
,那么怎样定价可使利润最大?
解 (1),
记,
由
解得.
(2)由得收益函数,
则利润函数
.
由,解得.
当时, ;当时, .
所以,当时,取得极小值,也是最小值,
也就是此时边际成本最低.
答 生产1000个单位产品时,边际成本最低;
当产品的单价为75时,利润最大.
?
当时,;
当时,.
所以,当时,利润最大,
此时.
用图象来表示有下列3种形式,这就是如何确定生产规模的一般数学模型.
一般地,为使利润函数最大,生产规模应确定为,且,即
练习
一列车队以速度行进,每辆车长,两车之间的合适间距为问:车速为多少时,单位时段内通过的汽车数量最多?
解 记两车间距为,其中,则一辆车占去的道路长为,
内通过汽车的数量为 .
由 ,解得
当0<时,;当时,.
因此,当时,取得极大值,也是最大值.
因此,当时,每小时通过的车辆数最多,约为辆.
课堂小结
求解实际应用题的步骤:
①仔细审题. 关注实际生活背景.
②建立数学模型. 建立函数模型,关注定义域.
③求解数学问题. 可以用导数法求解最值问题.
④检验并回答. 作答要符合问题要求.
导数在实际生活中的应用
苏教版教科书选修2-2《数学》
新课引入
导数在实际生活中有着广泛的应用,利用导数求最值的方法,可以解决实际生活中的某些最值问题.
1.几何方面的应用
2.物理方面的应用
3.经济学方面的应用
(如:面积、体积等最值问题)
(如:利润最大化问题等)
(如:功、功率等最值问题)
例1 在边长为60 cm的正方形铁片的四角切去边长相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱子容积最大?最大容积是多少?
例题分析
解 设箱底边长为,
则箱高为
箱子的容积为
由解得
当时,;当时,.
所以,函数在处取得极大值,
这个极大值就是函数的最大值,
即
答 当箱子底边长等于时,箱子容积最大,
最大值为
1.应用题解题基本步骤
解题回顾
2.本题利用了导数法求解容积最大问题
3.对于开区间内,如果函数只有一个极值,那么这个极值也是最值.
(2)建立数学模型;
(3)解答数学问题;
(4)检验并回答实际问题.
(1)仔细审题,明确题意;
例2 某种圆柱形饮料罐的容积一定,如何确定它的高与底半径,才能使它的用料最省?
解 设圆柱的高为,底半径为,
则表面积S=2
又圆柱体积(定值),则,故
由,解得
此时,,即
当时,;当时,
所以 ,当时,取得极小值,且是最小值.
答 当罐高与罐底的直径相等时,用料最省.
1.对于一个实际生活问题,我们需要将其转化为
数学问题,会用图形语言和数学符号语言表达问题.
解题回顾
2.出现两个或两个以上变量时,需要明确哪个字母是自变量,然后将其它变量用这个自变量表示,从而问题就转化成了一个单变量函数问题,我们再用导数法求这个函数的最值.
3.最后下结论时,要切合题目要求,准确回答.
练习
(1)求内接于半径为R的圆的矩形面积的最大值.
(2)求内接于半径为R的球的圆柱体积的最大值.
(1)求内接于半径为R的圆的矩形面积的最大值.
解 设矩形的一边长为,则另一边长为,
故矩形的面积为
令,对求导可得,.
令,可得.
当时,;当时,.
所以,当时,取得极大值,且为最大值,
此时,矩形面积取得最大值为
答 矩形面积的最大值为
(2)求内接于半径为R的球的圆柱体积的最大值.
解 设球内接圆柱的高为,圆柱底面半径为,
则
求导数,得.
当时,;当时,.
所以,当时,取得极大值,且为最大值,
此时,最大值为
答 圆柱的最大值为
故圆柱的体积为
1.导数在实际生活中的应用主要是解决有关最大(小)值问题;
2.解题时,先仔细审题,准确理解题意,将实际问题数学化,建立目标函数,然后用导数法求目标函数的最值,最后回到实际问题.
例3 在如图所示的电路中,已知电源的内阻为,电动势为.当外电阻为多大时,才能使电功率最大?最大电功率是多少?
解 电功率,其中为电流强度,
则.
例题解析
R
由,解得.
当时,;当R>时,
因此,当时,取得极大值,且是最大值,最大值为.
答 当外电阻等于内电阻时,电功率最大,最大电功率是
解题回顾
1.本题求解电功率的最大值问题用了导数法,
可见数学是物理研究的工具和手段.
2.解题中,出现多个字母时,要认清哪个是变量,
哪个是常量.
例4 强度分别为的两个点光源间的距离为,试问:在连结两光源的线段上,何处照度最小?试时回答上述问题.(照度与光的强度成正比,与光源距离的平方成反比)
解 如图,设点在线段上,且距光源为,则距光源为
点受光源的照度为,即;
点受光源的照度为,即,其中为比例常数.
从而,点的总照度为(0<<3).
由
解得 .
当<<时,<0;当<<时,>0.
因此,时取得极小值,且是最小值.
答 在连结两光源的线段上,距光源为处的照度最小.
我们特别要注意,
建立正确的目标函数的前提是准确理解题意.
例5 在经济学中,生产单位产品的成本称为成本函数,记为,出售单位产品的收益称为收益函数,记为, 称为利润函数,记为.
(1)如果,
那么生产多少单位产品时,边际成本最低?
(2)如果,产品的单价
,那么怎样定价可使利润最大?
解 (1),
记,
由
解得.
(2)由得收益函数,
则利润函数
.
由,解得.
当时, ;当时, .
所以,当时,取得极小值,也是最小值,
也就是此时边际成本最低.
答 生产1000个单位产品时,边际成本最低;
当产品的单价为75时,利润最大.
?
当时,;
当时,.
所以,当时,利润最大,
此时.
用图象来表示有下列3种形式,这就是如何确定生产规模的一般数学模型.
一般地,为使利润函数最大,生产规模应确定为,且,即
练习
一列车队以速度行进,每辆车长,两车之间的合适间距为问:车速为多少时,单位时段内通过的汽车数量最多?
解 记两车间距为,其中,则一辆车占去的道路长为,
内通过汽车的数量为 .
由 ,解得
当0<时,;当时,.
因此,当时,取得极大值,也是最大值.
因此,当时,每小时通过的车辆数最多,约为辆.
课堂小结
求解实际应用题的步骤:
①仔细审题. 关注实际生活背景.
②建立数学模型. 建立函数模型,关注定义域.
③求解数学问题. 可以用导数法求解最值问题.
④检验并回答. 作答要符合问题要求.
