沪科版数学九年级上册第21章 二次函数与反比例函数 热门考点整合应用习题 课件(49张ppt)
文档属性
| 名称 | 沪科版数学九年级上册第21章 二次函数与反比例函数 热门考点整合应用习题 课件(49张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-07 20:53:02 | ||
图片预览








文档简介
课件49张PPT。沪科版九年级上第21章 二次函数与反比例函数
全章热门考点整合应用
答案显示(1)-5或1.(2)1
(3)-5①③④DBC见习题BC答案显示见习题见习题B见习题1见习题见习题见习题答案显示见习题C见习题1.已知函数y=(m+3)xm2+4m-3+5是关于x的二次函数.
(1)求m的值;(2)当m为何值时,该函数图象的开口向上?
(3)当m为何值时,该函数有最大值?解:∵函数图象的开口向上,∴m+3>0.∴m>-3.
∴m=1.∴当m=1时,该函数图象的开口向上.∵函数有最大值,∴m+3<0,∴m<-3.∴m=-5.
∴当m=-5时,该函数有最大值.2.若y=(m-1)x|m|-2是反比例函数,则m的取值为( )
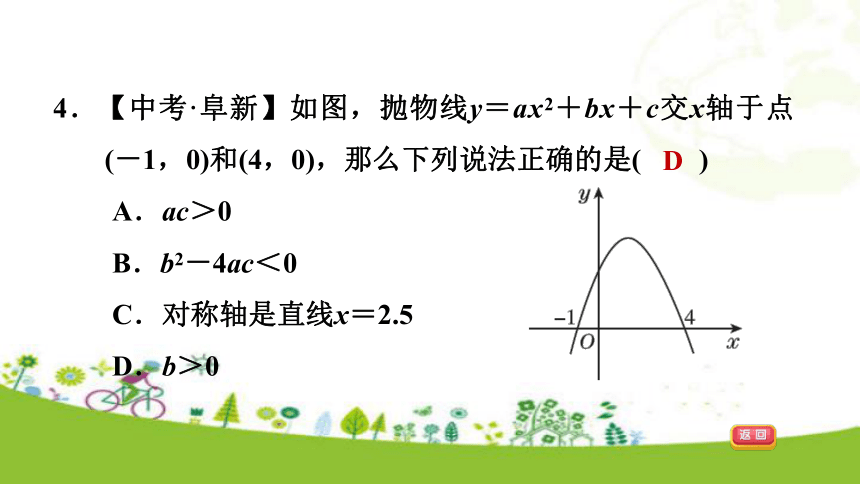
A.1 B.-1 C.±1 D.任意实数B①③④4.【中考·阜新】如图,抛物线y=ax2+bx+c交x轴于点(-1,0)和(4,0),那么下列说法正确的是( )
A.ac>0
B.b2-4ac<0
C.对称轴是直线x=2.5
D.b>0DC解:如图.
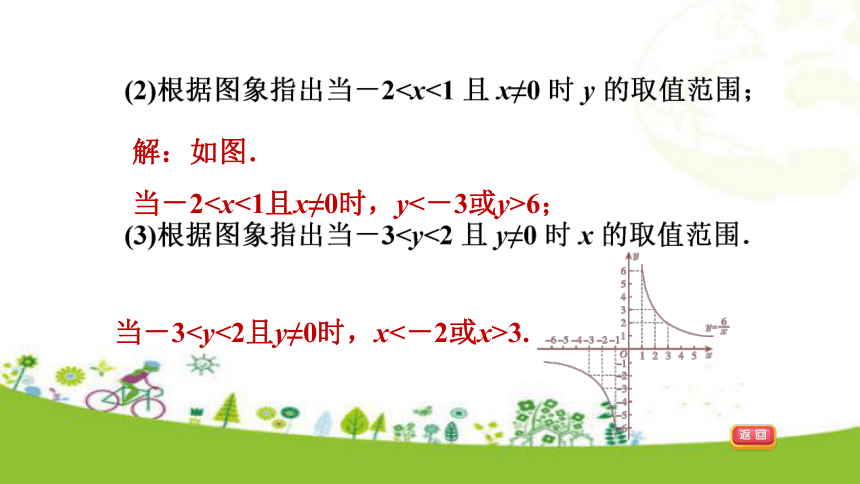
当y=-2时,x=-3;解:如图.
当-26;当-33.7.【中考·安顺】如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0;②2a+b=0;③a+b+c>0;④当-1<x<3时,y>0.其中正确的个数为( )
A.1 B.2
C.3 D.4【答案】C【答案】B【点拨】分类讨论思想是数学的常用思想,当问题中未明确是哪类函数时,通常要进行分类讨论.10.如图,有长为24 m的栅栏,一面利用墙(墙的最大可用长度为10 m),围成中间隔有一道栅栏的长方形鸡舍(栅栏厚度不计).设鸡舍的一边AB为x m,面积为S m2.
(1)求S与x的函数表达式(不必写出x的取值范围).解:∵AB=x m,∴BC=(24-3x) m,∴S=x(24-3x)=-3x2+24x.(2)如果围成面积为45 m2的鸡舍,AB的长是多少米?(3)能围成面积比45 m2更大的鸡舍吗?如果能,请求出最大面积;如果不能,请说明理由.11.跳绳时,绳甩到最高处时的形状可近似看作抛物线.正在甩绳的甲、乙两名同学拿绳的手间距(A与B间的水平距离)为6 m,到地面的距离AO和BD均为0.9 m,身高为1.4 m的小丽站在距点O的水平距离为1 m的点F处,绳子甩到最高处时刚好通过她的头顶点E.以点O为原点建立如图所示的平面直角坐标系,设此抛物线对应的函数表达式为
y=ax2+bx+0.9.(1)求该抛物线对应的函数表达式(不考虑自变量的取值范围);(2)如果小华站在O,D之间,且离点O的距离为3 m,当绳子甩到最高处时刚好通过他的头顶,请你算出小华的身高;解:把x=3代入y=-0.1x2+0.6x+0.9,
得y=-0.1×32+0.6×3+0.9=1.8.
即小华的身高是1.8 m.(3)如果身高为1.4 m的小丽站在O,D之间,且离点O的距离为t m,绳子甩到最高处时超过她的头顶,请结合图象,写出t的取值范围.解:当y=1.4时,-0.1x2+0.6x+0.9=1.4.解得x1=1,x2=5.
∴1<t<5.B13.2020年初,新冠肺炎疫情的爆发夺去了许多人的生命.某公司为了员工们的身心健康,在休息日用药薰消毒法对办公场所进行消毒.已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分)成正比例,药物释放过程
中,y与x成反比例.如图所示,根据题
中提供的信息,答案下列问题:(1)写出从药物燃烧到释放过程中,y与x之间的
两个函数关系式及相应的自变量的取值范围;解:设药物燃烧时y关于x的函数关系式为y=k1x(k1 >0) ,代人(12,9)为9=12k1,解得
设药物燃烧后y关于x的函数关系式为
代入(12,9)为 解得k2=108.
所以药物燃烧时y关于x的函数关系式为
药物燃烧后y关于x的函数关系式为(2)据测定,当空气中每立方米的含药量低于阶
0.45毫克以下时,人员方可人室,那么从药物
燃烧开始,至少需要经过多少分钟后,人员才能
进人室内?解:结合实际,令 y≤0.45,解得x≥240.即从药物燃烧开始,至少需要经过
240分钟后,学生才能进人.14.如图,线段AB的长为2,点C为AB上一个动点,分别以AC,BC为斜边在AB的同侧作等腰直角三角形ACD和等腰直角三角形BCE,求DE长的最小值.(2)求四边形ODPC的面积.16.某市“建设社会主义新农村”工作组到某县大棚蔬菜生产基地指导菜农修建大棚种植蔬菜.通过调查得知,修建大棚平均每公顷要用支架、农膜等材料费2.7万元;购置滴灌设备的费用(万元)与大棚面积(公顷)的平方成正比,比例系数为0.9;另外,种植蔬菜每公顷需种子、化肥、农药等开支0.3万元.每公顷蔬菜年均可卖7.5万元.(1)某基地的菜农共修建大棚x公顷,当年收益(扣除修建和种植成本后)为y万元,写出y关于x的函数表达式;解:y=7.5x-(2.7x+0.9x2+0.3x)=-0.9x2+4.5x.(2)除种子、化肥、农药等投资只能当年使用外,其他设施3年内不需要增加投资仍可继续使用.如果按3年计算,是否修建大棚面积越大,收益就越大?如果不是,修建面积为多少时可以获得最大收益?请帮助工作组为基地修建大棚提一条合理化的建议.解:设3年内每年的平均收益为z万元,根据题意,得
z=7.5x-(0.9x+0.3x2+0.3x)=-0.3x2+6.3x=-0.3(x-10.5)2+33.075.所以并不是面积越大收益就越大,当修建面积为10.5公顷时可以获得最大收益.
建议略.17.【2019·天津】二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的自变量x与函数值y的部分对应值如下表:C18.如图,把矩形OABC放入平面直角坐标系中,使OA,OC分别落在x轴、y轴上,连接OB,将矩形OABC沿OB折叠,使点A落在点A′处,A′B与y轴交于点F.已知OA=1,AB=2.
(1)设CF=x,则OF=________;
(2)求BF的长;
(3)设过点B的双曲线为l,试问:双曲线l上是否存在一点M,使得△OBM的面积等于1?若存在,试求出点M的横坐标;若不存在,试说明理由.【点拨】已知三角形的一边时,可在这条边的两侧作三角形.要注意分类讨论,不要漏掉任何一种情况.(1)设CF=x,则OF=________;
(2)求BF的长;2-x(3)设过点B的双曲线为l,试问:双曲线l上是否存在一点M,使得△OBM的面积等于1?若存在,试求出点M的横坐标;若不存在,试说明理由.19.【中考·安徽】如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).
(1)求a,b的值;(2)点C是该二次函数图象上A,B两点之间的一个动点,横坐标为x(2<x<6),写出四边形OACB的面积S关于点C的横坐标x的函数表达式,并求S的最大值.谢谢!
全章热门考点整合应用
答案显示(1)-5或1.(2)1
(3)-5①③④DBC见习题BC答案显示见习题见习题B见习题1见习题见习题见习题答案显示见习题C见习题1.已知函数y=(m+3)xm2+4m-3+5是关于x的二次函数.
(1)求m的值;(2)当m为何值时,该函数图象的开口向上?
(3)当m为何值时,该函数有最大值?解:∵函数图象的开口向上,∴m+3>0.∴m>-3.
∴m=1.∴当m=1时,该函数图象的开口向上.∵函数有最大值,∴m+3<0,∴m<-3.∴m=-5.
∴当m=-5时,该函数有最大值.2.若y=(m-1)x|m|-2是反比例函数,则m的取值为( )
A.1 B.-1 C.±1 D.任意实数B①③④4.【中考·阜新】如图,抛物线y=ax2+bx+c交x轴于点(-1,0)和(4,0),那么下列说法正确的是( )
A.ac>0
B.b2-4ac<0
C.对称轴是直线x=2.5
D.b>0DC解:如图.
当y=-2时,x=-3;解:如图.
当-2
A.1 B.2
C.3 D.4【答案】C【答案】B【点拨】分类讨论思想是数学的常用思想,当问题中未明确是哪类函数时,通常要进行分类讨论.10.如图,有长为24 m的栅栏,一面利用墙(墙的最大可用长度为10 m),围成中间隔有一道栅栏的长方形鸡舍(栅栏厚度不计).设鸡舍的一边AB为x m,面积为S m2.
(1)求S与x的函数表达式(不必写出x的取值范围).解:∵AB=x m,∴BC=(24-3x) m,∴S=x(24-3x)=-3x2+24x.(2)如果围成面积为45 m2的鸡舍,AB的长是多少米?(3)能围成面积比45 m2更大的鸡舍吗?如果能,请求出最大面积;如果不能,请说明理由.11.跳绳时,绳甩到最高处时的形状可近似看作抛物线.正在甩绳的甲、乙两名同学拿绳的手间距(A与B间的水平距离)为6 m,到地面的距离AO和BD均为0.9 m,身高为1.4 m的小丽站在距点O的水平距离为1 m的点F处,绳子甩到最高处时刚好通过她的头顶点E.以点O为原点建立如图所示的平面直角坐标系,设此抛物线对应的函数表达式为
y=ax2+bx+0.9.(1)求该抛物线对应的函数表达式(不考虑自变量的取值范围);(2)如果小华站在O,D之间,且离点O的距离为3 m,当绳子甩到最高处时刚好通过他的头顶,请你算出小华的身高;解:把x=3代入y=-0.1x2+0.6x+0.9,
得y=-0.1×32+0.6×3+0.9=1.8.
即小华的身高是1.8 m.(3)如果身高为1.4 m的小丽站在O,D之间,且离点O的距离为t m,绳子甩到最高处时超过她的头顶,请结合图象,写出t的取值范围.解:当y=1.4时,-0.1x2+0.6x+0.9=1.4.解得x1=1,x2=5.
∴1<t<5.B13.2020年初,新冠肺炎疫情的爆发夺去了许多人的生命.某公司为了员工们的身心健康,在休息日用药薰消毒法对办公场所进行消毒.已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分)成正比例,药物释放过程
中,y与x成反比例.如图所示,根据题
中提供的信息,答案下列问题:(1)写出从药物燃烧到释放过程中,y与x之间的
两个函数关系式及相应的自变量的取值范围;解:设药物燃烧时y关于x的函数关系式为y=k1x(k1 >0) ,代人(12,9)为9=12k1,解得
设药物燃烧后y关于x的函数关系式为
代入(12,9)为 解得k2=108.
所以药物燃烧时y关于x的函数关系式为
药物燃烧后y关于x的函数关系式为(2)据测定,当空气中每立方米的含药量低于阶
0.45毫克以下时,人员方可人室,那么从药物
燃烧开始,至少需要经过多少分钟后,人员才能
进人室内?解:结合实际,令 y≤0.45,解得x≥240.即从药物燃烧开始,至少需要经过
240分钟后,学生才能进人.14.如图,线段AB的长为2,点C为AB上一个动点,分别以AC,BC为斜边在AB的同侧作等腰直角三角形ACD和等腰直角三角形BCE,求DE长的最小值.(2)求四边形ODPC的面积.16.某市“建设社会主义新农村”工作组到某县大棚蔬菜生产基地指导菜农修建大棚种植蔬菜.通过调查得知,修建大棚平均每公顷要用支架、农膜等材料费2.7万元;购置滴灌设备的费用(万元)与大棚面积(公顷)的平方成正比,比例系数为0.9;另外,种植蔬菜每公顷需种子、化肥、农药等开支0.3万元.每公顷蔬菜年均可卖7.5万元.(1)某基地的菜农共修建大棚x公顷,当年收益(扣除修建和种植成本后)为y万元,写出y关于x的函数表达式;解:y=7.5x-(2.7x+0.9x2+0.3x)=-0.9x2+4.5x.(2)除种子、化肥、农药等投资只能当年使用外,其他设施3年内不需要增加投资仍可继续使用.如果按3年计算,是否修建大棚面积越大,收益就越大?如果不是,修建面积为多少时可以获得最大收益?请帮助工作组为基地修建大棚提一条合理化的建议.解:设3年内每年的平均收益为z万元,根据题意,得
z=7.5x-(0.9x+0.3x2+0.3x)=-0.3x2+6.3x=-0.3(x-10.5)2+33.075.所以并不是面积越大收益就越大,当修建面积为10.5公顷时可以获得最大收益.
建议略.17.【2019·天津】二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的自变量x与函数值y的部分对应值如下表:C18.如图,把矩形OABC放入平面直角坐标系中,使OA,OC分别落在x轴、y轴上,连接OB,将矩形OABC沿OB折叠,使点A落在点A′处,A′B与y轴交于点F.已知OA=1,AB=2.
(1)设CF=x,则OF=________;
(2)求BF的长;
(3)设过点B的双曲线为l,试问:双曲线l上是否存在一点M,使得△OBM的面积等于1?若存在,试求出点M的横坐标;若不存在,试说明理由.【点拨】已知三角形的一边时,可在这条边的两侧作三角形.要注意分类讨论,不要漏掉任何一种情况.(1)设CF=x,则OF=________;
(2)求BF的长;2-x(3)设过点B的双曲线为l,试问:双曲线l上是否存在一点M,使得△OBM的面积等于1?若存在,试求出点M的横坐标;若不存在,试说明理由.19.【中考·安徽】如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).
(1)求a,b的值;(2)点C是该二次函数图象上A,B两点之间的一个动点,横坐标为x(2<x<6),写出四边形OACB的面积S关于点C的横坐标x的函数表达式,并求S的最大值.谢谢!
