鲁教版(五四制)数学九年级上册第二章 直角三角形的边角关系 热门考点整合应用习题 课件(24张ppt)
文档属性
| 名称 | 鲁教版(五四制)数学九年级上册第二章 直角三角形的边角关系 热门考点整合应用习题 课件(24张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-04 22:39:55 | ||
图片预览







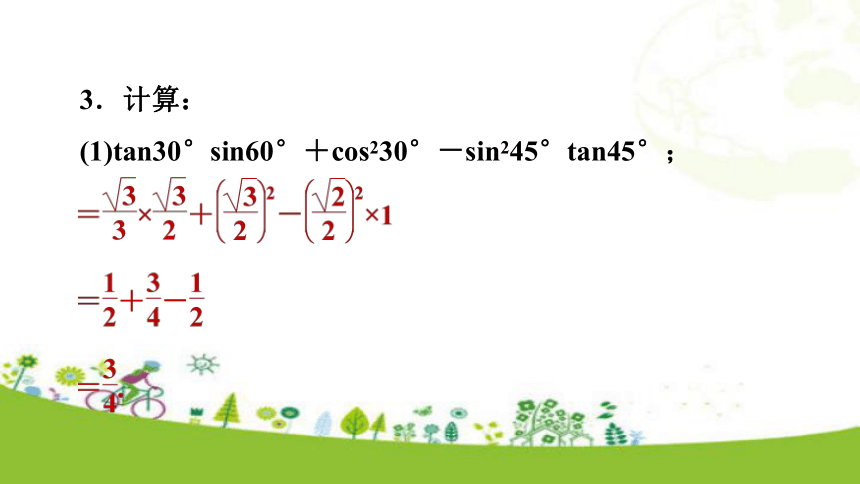
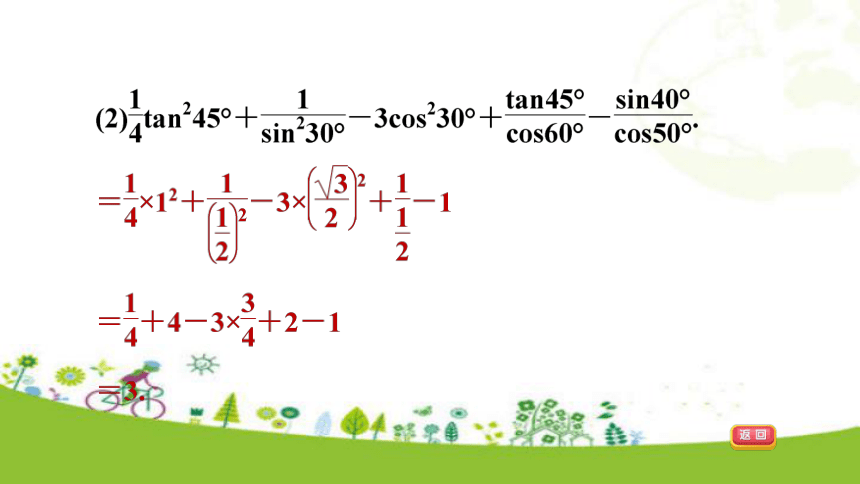
文档简介
课件24张PPT。鲁教版九年级上全章热门考点整合应用第二章 直角三角形的边角关系答案显示见习题51.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,CD⊥AB于点D,求∠BCD的三个三角函数值.【思路导引】求∠BCD的三个三角函数值,关键要
弄清它们的定义.由于∠BCD是Rt△BCD中的
一个内角,根据定义,仅一边BC是已知的,此时有两条路可走,一是设法求出BD或CD,二是把∠BCD转化成∠A.显然走第二条路较方便,因为在Rt△ABC中,三边均可得出,利用三角函数的定义即可求出答案.【点拨】方程思想是一种重要的思想方法,运用方程思想可以建立已知量和待求量之间的关系式.3.计算:
(1)tan30°sin60°+cos230°-sin245°tan45°;4.如图,在矩形ABCD中,AB=4,AD=5,P是射线BC上的一个动点,过点P作PE⊥AP,交射线DC于点E,射线AE交射线BC于点F,设BP=a.
(1)当点P在线段BC上时(点P与点B,C都不重合),试用含a的代数式表示CE的长; (2)当a=3时,连接DF,试判断四边形APFD的形状,并说明理由;5.【中考·成都】科技改变生活,手机导航极大方便了人们的出行,如图,小明一家自驾到古镇C游玩,到达A地后,导航显示车辆应沿北偏西60°方向行驶4 km至B地,再沿北偏东45°方向行驶一段距离到达古镇C,小明发现古镇C恰好在A地的
正北方向,求B,C两地的距离.6.【中考·黄冈】如图,在大楼AB正前方有一斜坡CD,坡角∠DCE=30°,楼高AB=60米,在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A,C,E在同一直线上.
(1)求坡底C点到大楼距离AC的值;
(2)求斜坡CD的长度.方法总结:在不含直角三角形的图形中,求与三角形有关的线段长、非特殊角的某个三角函数、面积等问题,一般可通过分割图形、作高等方法,把问题转化为解直角三角形来解决,巧妙合理地做出辅助线是解此类题的关键.谢谢!
弄清它们的定义.由于∠BCD是Rt△BCD中的
一个内角,根据定义,仅一边BC是已知的,此时有两条路可走,一是设法求出BD或CD,二是把∠BCD转化成∠A.显然走第二条路较方便,因为在Rt△ABC中,三边均可得出,利用三角函数的定义即可求出答案.【点拨】方程思想是一种重要的思想方法,运用方程思想可以建立已知量和待求量之间的关系式.3.计算:
(1)tan30°sin60°+cos230°-sin245°tan45°;4.如图,在矩形ABCD中,AB=4,AD=5,P是射线BC上的一个动点,过点P作PE⊥AP,交射线DC于点E,射线AE交射线BC于点F,设BP=a.
(1)当点P在线段BC上时(点P与点B,C都不重合),试用含a的代数式表示CE的长; (2)当a=3时,连接DF,试判断四边形APFD的形状,并说明理由;5.【中考·成都】科技改变生活,手机导航极大方便了人们的出行,如图,小明一家自驾到古镇C游玩,到达A地后,导航显示车辆应沿北偏西60°方向行驶4 km至B地,再沿北偏东45°方向行驶一段距离到达古镇C,小明发现古镇C恰好在A地的
正北方向,求B,C两地的距离.6.【中考·黄冈】如图,在大楼AB正前方有一斜坡CD,坡角∠DCE=30°,楼高AB=60米,在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A,C,E在同一直线上.
(1)求坡底C点到大楼距离AC的值;
(2)求斜坡CD的长度.方法总结:在不含直角三角形的图形中,求与三角形有关的线段长、非特殊角的某个三角函数、面积等问题,一般可通过分割图形、作高等方法,把问题转化为解直角三角形来解决,巧妙合理地做出辅助线是解此类题的关键.谢谢!
