2019—2020学年新人教版必修第二册 第六章 圆周运动 单元检测试题3(解析版)
文档属性
| 名称 | 2019—2020学年新人教版必修第二册 第六章 圆周运动 单元检测试题3(解析版) | 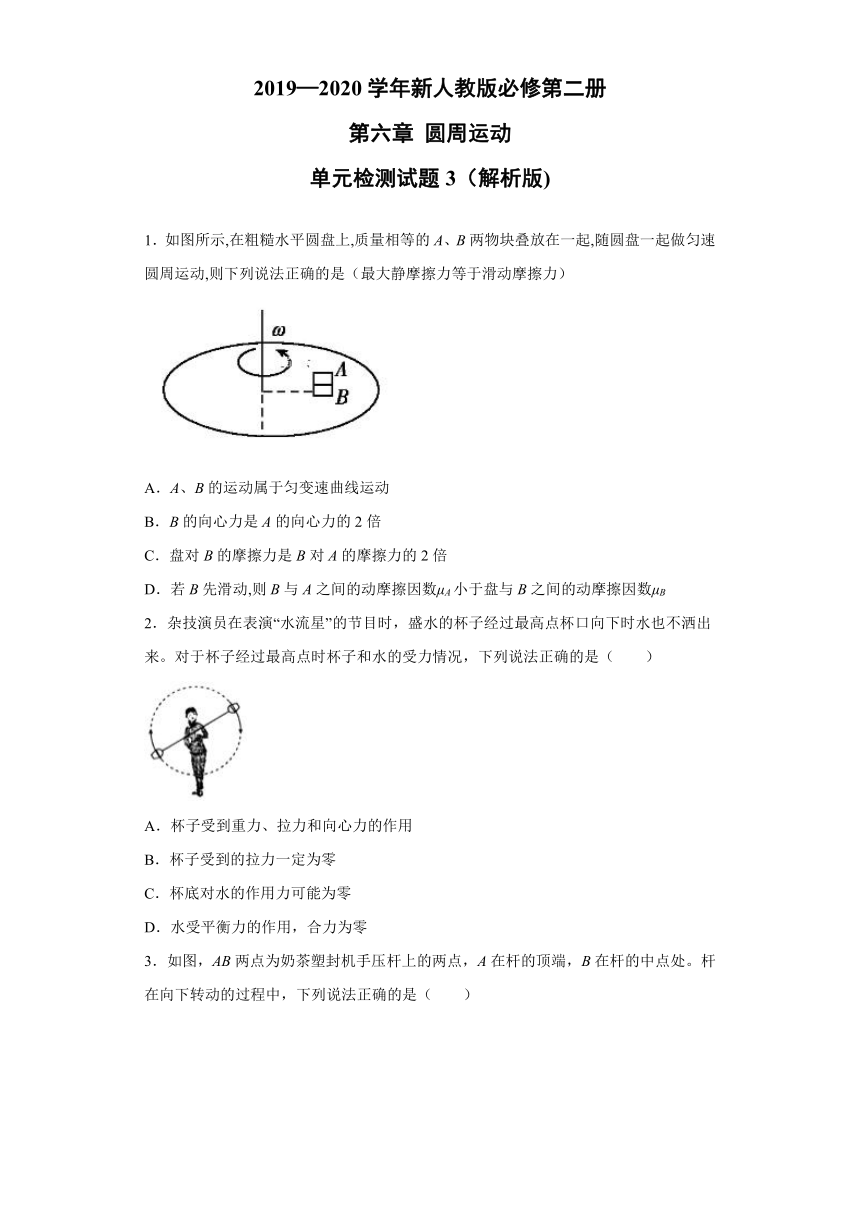 | |
| 格式 | zip | ||
| 文件大小 | 383.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-04-04 12:30:28 | ||
图片预览




文档简介
2019—2020学年新人教版必修第二册
第六章 圆周运动
单元检测试题3(解析版)
1.如图所示,在粗糙水平圆盘上,质量相等的A、B两物块叠放在一起,随圆盘一起做匀速圆周运动,则下列说法正确的是(最大静摩擦力等于滑动摩擦力)
A.A、B的运动属于匀变速曲线运动
B.B的向心力是A的向心力的2倍
C.盘对B的摩擦力是B对A的摩擦力的2倍
D.若B先滑动,则B与A之间的动摩擦因数μA小于盘与B之间的动摩擦因数μB
2.杂技演员在表演“水流星”的节目时,盛水的杯子经过最高点杯口向下时水也不洒出来。对于杯子经过最高点时杯子和水的受力情况,下列说法正确的是( )
A.杯子受到重力、拉力和向心力的作用
B.杯子受到的拉力一定为零
C.杯底对水的作用力可能为零
D.水受平衡力的作用,合力为零
3.如图,AB两点为奶茶塑封机手压杆上的两点,A在杆的顶端,B在杆的中点处。杆在向下转动的过程中,下列说法正确的是( )
A.A、B两点线速度大小之比为1:2
B.A、B两点角速度大小之比为1:1
C.A、B两点周期大小之比为2:1
D.A、B两点向心加速度大小之比为1:1
4.如图所示,质量为m的小球置于正方体的光滑盒子中,盒子的边长略大于球的直径。某同学拿着该盒子在竖直平面内做半径为R的匀速圆周运动,已知重力加速度为g,空气阻力不计,要使在最高点时盒子与小球之间恰好无作用力,则( )
A.该盒子做圆周运动的向心力一定恒定不变
B.该盒子做匀速圆周运动的周期一定等于2
C.盒子在最低点时,小球对盒子的作用力大小等于mg
D.盒子在与O点等高的右侧位置时,小球对盒子的作用力大小等于mg
5.如图所示,长为L的轻杆,一端固定一个质量为m的小球,另一端固定在水平转轴O上,现让杆绕转轴O在竖直平面内匀速转动,角速度为,某时刻杆对球的作用力恰好与杆垂直,则此时杆与水平面的夹角满足( )
A.
B.
C.
D.
6.如图所示,物块m随转筒一起以角速度做匀速圆周运动,如下描述正确的是( )
A.物块受到重力、弹力、摩擦力和向心力的作用
B.若角速度增大而且物块仍然随转筒一起做匀速圆周运动,那么物块所受弹力增大
C.若角速度增大而且物块仍然随转筒一起做匀速圆周运动,物块所受摩擦力增大
D.若角速度增大而且物块仍然随转筒一起做匀速圆周运动,物块所受摩擦力不变
7.如图甲所示是一种利用霍尔效应传感器测量运动速率的自行车速度计。车轮每转一周,安装在自行车前轮上的一块磁铁就靠近霍尔传感器一次,产生一次电压脉冲。图乙为某次骑行中记录的脉冲电压U与时间t的图象。已知自行车车轮的半径为33cm,磁铁与轮轴的距离为车轮半径的0.75倍,则该自行车( )
A.车轮边缘与磁铁的线速度大小相等
B.在1.0s~1.4s内,速率几乎不变
C.在1.4s~2.2s内做减速运动
D.在1.2s时的速率约为10m/s
8.如图所示,水平转台上有一个质量为m的物块,用长为L的细线将物块连接在转轴上,细线与竖直转轴的夹角为θ,此时细线中张力为零,物块与转台间的动摩擦因数为μ(),最大静摩擦力等于滑动摩擦力,物块随转台由静止开始缓慢加速转动,则下列说法正确的是( )
A.转台一开始转动,细线立即绷直对物块施加拉力
B.当细线中出现拉力时,转台对物块做的功为
C.当物体的角速度为时,转台对物块的支持力为零
D.当转台对物块的支持力刚好为零时,转台对物块做的功为
9.有关圆周运动的基本模型,下列说法正确的是( )
A.如图a,汽车通过拱桥的最高点处于超重状态
B.如图b所示是一圆锥摆,增大θ,若保持圆锥的高不变,则圆锥摆的角速度不变
C.如图c,同一小球在光滑而固定的圆锥筒内的A、B位置先后分别做匀速圆周运动,则在A、B两位置小球的角速度及所受筒壁的支持力大小相等
D.火车转弯超过规定速度行驶时,外轨对火车轮缘会有挤压作用
10.如图所示,竖直平面内固定有一个半径为R的光滑圆环形细管,现给小球(直径略小于管内径)一个初速度,使小球在管内做圆周运动,小球通过最高点时的速度为v,已知重力加速度为g , 则下列叙述中正确的是( )
A.v的极小值为
B.v由零逐渐增大的过程中,轨道对球的弹力先减小再增大
C.当v由值逐渐增大的过程中,轨道对小球的弹力也逐渐增大
D.当v由值逐渐减小的过程中,轨道对小球的弹力也逐渐减小
11.某探究小组用能够显示并调节转动频率的小电动机验证匀速圆周运动的向心力关系式。
(1)如图所示,把转动频率可调的小电动机固定在支架上,转轴竖直向下,将摇臂平台置于小电动机正下方的水平桌面上
(2)在转动轴正下方固定一不可伸长的细线,小电动机转轴与细线连接点记为O。细线另一端穿过小铁球的球心并固定
(3)启动电动机,记录电动机的转动频率f,当小球转动稳定时,将摇臂平台向上移动,无限接近转动的小球
(4)关闭电动机,测量O点到摇臂平台的高度h
(5)改变电动机的转动频率,重复上述实验。本实验______(选填“需要”或“不需要)测量小球的质量。请你根据所记录的O点到摇臂平台的高度h和小球的直径D,重力加速度为g,若所测物理量满足g=_____,则成立。(用所测物理量符号表示)
12.一个喷漆桶能够向外喷射不同速度的油漆雾滴,,某同学决定测量雾滴的喷射速度,他采用如图1所示的装置,一个直径为d=40cm的纸带环,安放在一个可以按照不同转速转动的固定转台上,纸带环上刻有一条狭缝A,在狭缝A的正对面画一条标志线.如图1所示.在转台达到稳定转速时,向侧面同样开有狭缝B的纸盒中喷射油漆雾滴,当狭缝A转至与狭缝B正对平行时,雾滴便通过狭缝A在纸带的内侧面留下痕迹.将纸带从转台上取下来,展开平放,并与毫米刻度尺对齐,如图图2所示.
请你帮该同学完成下列任务:(只保留2位有效数字)
(1)设喷射到纸带上的油漆雾滴痕迹到标志线的距离为s,则从图2可知,其中速度最大的雾滴到标志线的距离s1=__cm;速度最小的雾滴到标志线的距离s2=______cm.
(2)如果转台转动的周期为T,则这些雾滴喷射速度范围的计算表达式为v0=_______(用字母表示)
(3)如果以纵坐标表示雾滴速度v0、横坐标表示雾滴距标志线距离的倒数,画出v0一图线,如图3所示,则可知转台转动的周期为T=________s.
13.如图所示,AB为竖直转轴,细绳AC 和BC 的结点C系一质量为m的小球,两绳能承担的最大拉力均为2mg。当AC和BC均拉直时,,。ABC能绕竖直轴AB匀速转动,因而C球在水平面内做匀速圆周运动。当小球的线速度增大时,两绳均会被拉断,求:
(1)哪根绳最先被拉断,被拉断时的线速度v1;
(2)另一根绳被拉断时的速度v2。(已知,,)
14.质量为的小球固定在长为的轻绳一端,绳子可绕O点的水平转轴在竖直平面内转动。,求:
(1)小球在最高点的最小速度;
(2)在最低点小球速度为9m/s时,绳中拉力为多大?
15.如图所示,轻杆长为3L,在杆的A、B两端分别固定质量均为m的球A和球B,杆上距球A为L处的点O装在光滑水平转动轴上,杆和球在竖直面内转动,已知球A运动到最高点时,球A的速度刚好为。求:
(1)球A在最高点时的角速度大小;
(2)杆此时对球B作用力大小和方向。
16.如图所示,装置可绕竖直轴转动,可视为质点的小球A与两细线连接后分别系于B、C两点,装置静止时细线AB水平,细线AC与竖直方向的夹角θ=37°.已知小球的质量m=1kg,细线AC 长L=1m,B点距C点的水平和竖直距离相等.(g取10m/s2,sin37o=0.6,cos37o=0.8,结果可用根式表达)
(1)若装置匀速转动的角速度为ω1,细线AB上的张力为零而细线AC与竖直方向夹角仍为37°,求角速度ω1的大小;
(2)若装置以ω2匀速转动时,细线AB刚好竖直且张力为零,求此时角速度ω2的大小;
参考答案
1.C
【解析】
【详解】
A. 与都做匀速圆周运动,它们的加速度的方向是不断变化的,不是匀变速运动,故A错误;
B. 、两物体一起做匀速圆周运动,质量相等,角速度相等,转动的半径相等,根据可知、的向心力相等,故B错误;
C.对分析,有:
对整体分析:
可知盘对的摩擦力是对摩擦力的2倍,故C正确;
D. 对整体分析有:
解得:
对分析有:
解得:
因为先滑动,可知先达到临界角速度,可知的临界角速度较小,即有:
故D错误。
2.C
【解析】
【详解】
A.由于向心力是效果力,故A错误;
B.当在最点时速度为时,杯子不受拉力的作用,当速度大于时,杯子受到拉力的作用,故B错误;
C.当在最点时的速度为,则在最高点,水靠重力提供向心力,杯底对水的作用力为零,故C正确;
D.在最高点,水靠重力和弹力的合力提供向心力,合力不为零,故D错误。
3.B
【解析】
【分析】
【详解】
AB.A、B两点属于同轴转动,则A、B角速度相等,由于
根据公式可知,A、B两点线速度大小之比为2:1,故A错误,B正确;
C.由于A、B角速度相等,由公式可知,A、B两点周期大小之比为1:1,故C错误;
D.由于A、B角速度相等,由公式可知,A、B两点向心加速度大小之比为2:1,故D错误。
故选B。
4.B
【解析】
【分析】
【详解】
A.向心力的方向始终指向圆心,是变化的,故A错误;
B.在最高点,由
周期
故B正确;
C.盒子在最低点,由
可得
F=2mg
故C错误;
D.盒子在与O点等高的右侧位置时,盒子底部对小球的支持力等于小球的重力mg,而盒子侧壁的支持力也等于mg,两者相互垂直,所以盒子对小球的作用力等于mg,根据牛顿第三定律,小球对盒子的作用力大小等于mg,故D错误。
故选B。
5.A
【解析】
【详解】
小球所受重力和杆子的作用力的合力提供向心力,受力如图所示;
根据牛顿第二定律有:
,
解得:
,
AC.,A正确C错误;
BD.求出来是的表达式,而并非的表达式,BD错误.
6.BD
【解析】
【分析】
【详解】
A.因为物块始终随圆筒做匀速圆周运动,所以物块受重力G、静摩擦力F静和筒壁的弹力FN,筒壁的弹力FN充当了物块随圆筒做匀速圆周运动的向心力,故A错误;
B.若角速度增大而且物块仍然随转筒一起做匀速圆周运动时,筒壁的弹力FN=m2r,随着角速度增大,物块所受弹力FN增大,故B正确;
CD.当角速度增大而且物块仍然随转筒一起做匀速圆周运动时,在竖直方向物块受的重力G与静摩擦力F静二力平衡,F静=G,即物块所受摩擦力不变,故C错误,D正确.
故选BD。
7.BCD
【解析】
【分析】
【详解】
A. 根据题意知车轮边缘与磁铁具有相同的角速度,由圆周运动的公式v=r知,车轮边缘的线速度大于磁铁的线速度,故A错误;
B.车轮每转一周,安装在自行车前轮上的一块磁铁就靠近霍尔传感器一次,产生一次电压脉冲,根据记录的脉冲电压U与时间t的图像知,在1.0s~1.4s内记录的脉冲电压U与时间t的时间间隔相等,所以在1.0s~1.4s内,速率几乎不变,故B正确;
C. 根据记录的脉冲电压U与时间t的图像知,在1.4s~2.2s内记录的脉冲电压U与时间t的时间间隔增大,所以该自行车在1.4s~2.2s内做减速运动,故C正确;
D.已知自行车车轮的半径为33cm,在1.0s~1.4s内车轮每转一周的时间为0.2s,则在1.2s时的速率约为
故D正确。
故选BCD。
8.BD
【解析】
【详解】
AB.转台刚开始转动,细线未绷紧,此时静摩擦力提供向心力,当转动到某一角速度ω1时,静摩擦力达到最大值,根据牛顿第二定律,有
此时物块线速度大小为
从开始运动到细线中将要出现拉力过程中,设转台对物块做的功为W,对物块由动能定理,可得
联立解得
故A错误,B正确;
CD.当转台对物块支持力恰好为零时,竖直方向
水平方向
联立解得
此时物块的线速度大小为
从开始运动到转台对物块的支持力刚好为零过程中,设转台对物块做的功为W2,对物块由动能定理,可得
联立解得
故C错误,D正确。
故选BD。
9.BD
【解析】
【详解】
A.当汽车在拱桥顶端时,根据牛顿第二定律则有
可得
根据牛顿第三定律可得汽车通过拱桥的最高点处汽车对桥顶的压力小于重力,处于失重状态,故A错误;
B.球受到重力和绳的拉力作用,二者合力提供向心力,向心力大小为
小球做圆周运动的半径为
由牛顿第二定律得
联立可得角速度
知保持圆锥摆的高度不变,则角速度不变,故B正确;
C.设支持力与竖直方向的夹角为,则支持力的大小
则有
由牛顿第二定律得
可得角速度
由于,所以可得
故C错误;
D.火车拐弯时超过规定速度行驶时,由于支持力和重力的合力不够提供向心力,会对外轨产生挤压,即外轨对轮缘会有挤压作用,故D正确;
故选BD。
10.BC
【解析】
【详解】
由题可知,v的极小值为0,选项A错误;当v的范围在0-范围内逐渐变大时,根据可知,FN逐渐减小;当v在大于范围内逐渐变大时,根据可知,FN逐渐变大; 故选项BC正确,D错误;故选BC.
11.不需要
【解析】
【分析】
【详解】
[1][2].设细线与竖宜方向的夹角为,根据实验原理可得
由几何关系得
联立以上三式解得
根据上式可知,实验中不需要测量小球的质量。
12.
【解析】
(1) 雾滴运动的路程一定,速度越大,运行的时间越短,此时转台转过的弧度越小,打在纸带上的点距离标志线的距离越小.所以其中速度最大的雾滴到标志线的距离S1=2.10cm;速度最小的雾滴到标志线的距离S2=2.90cm;
(2) 如果转台转动的周期为T,则雾滴运动的时间为,所以
(3)图象中斜率,可得T=1.6s.
【点睛】解决本题的关键知道雾滴运动的路程一定,速度越大,运行的时间越短,此时转台转过的弧度越小,打在纸带上的点距离标志线的距离越小.会根据求出雾滴运动的时间,再根据求出喷枪喷出雾滴的速度.
13.(1)BC先断,;(2)
【解析】
【分析】
【详解】
(1)当绳子拉直时,线速度再增大时,不变,而增大,所以BC绳先断,当时,根据向心力公式得
解得
(2)当BC线断后,小球线速度继续增大,当时,AC也断。设此时AC线与竖直方向夹角,则有
代入数据解得
,
14.(1)3m/s;(2)20N
【解析】
【分析】
【详解】
(1)小球在最高点只受重力时,速度最小,有
解得
(2)在最低点拉力和重力合力提供向心力,有
解得
15.(1) ;(2)3mg;竖直向上
【解析】
【分析】
【详解】
(1)根据可得球A在最高点时的角速度大小
(2)由于A、B两球共轴转动,此时有
对杆B受力分析,根据牛顿第二定律得
解得
方向竖直向上
16.(1);(2).
【解析】
【分析】
【详解】
(1)细线AB上张力恰为零时,小球所受合外力为mgtan37°,应用牛顿第二定律可得:mgtan37°=mω12Lsin37° 解得:
(2)装置静止时细线AB水平,细线AC与竖直方向的夹角θ=37°,B点距C点的水平和竖直距离相等,所以,B点到OO′的距离为d=Lcos37°=0.8m;若装置以ω2匀速转动时,细线AB刚好竖直且张力为零,则细线与OO′之间的夹角为θ′,由几何关系得: ,则有:θ′=53° 应用牛顿第二定律可得mgtanθ′=mω22Lsinθ′ 解得: .
第六章 圆周运动
单元检测试题3(解析版)
1.如图所示,在粗糙水平圆盘上,质量相等的A、B两物块叠放在一起,随圆盘一起做匀速圆周运动,则下列说法正确的是(最大静摩擦力等于滑动摩擦力)
A.A、B的运动属于匀变速曲线运动
B.B的向心力是A的向心力的2倍
C.盘对B的摩擦力是B对A的摩擦力的2倍
D.若B先滑动,则B与A之间的动摩擦因数μA小于盘与B之间的动摩擦因数μB
2.杂技演员在表演“水流星”的节目时,盛水的杯子经过最高点杯口向下时水也不洒出来。对于杯子经过最高点时杯子和水的受力情况,下列说法正确的是( )
A.杯子受到重力、拉力和向心力的作用
B.杯子受到的拉力一定为零
C.杯底对水的作用力可能为零
D.水受平衡力的作用,合力为零
3.如图,AB两点为奶茶塑封机手压杆上的两点,A在杆的顶端,B在杆的中点处。杆在向下转动的过程中,下列说法正确的是( )
A.A、B两点线速度大小之比为1:2
B.A、B两点角速度大小之比为1:1
C.A、B两点周期大小之比为2:1
D.A、B两点向心加速度大小之比为1:1
4.如图所示,质量为m的小球置于正方体的光滑盒子中,盒子的边长略大于球的直径。某同学拿着该盒子在竖直平面内做半径为R的匀速圆周运动,已知重力加速度为g,空气阻力不计,要使在最高点时盒子与小球之间恰好无作用力,则( )
A.该盒子做圆周运动的向心力一定恒定不变
B.该盒子做匀速圆周运动的周期一定等于2
C.盒子在最低点时,小球对盒子的作用力大小等于mg
D.盒子在与O点等高的右侧位置时,小球对盒子的作用力大小等于mg
5.如图所示,长为L的轻杆,一端固定一个质量为m的小球,另一端固定在水平转轴O上,现让杆绕转轴O在竖直平面内匀速转动,角速度为,某时刻杆对球的作用力恰好与杆垂直,则此时杆与水平面的夹角满足( )
A.
B.
C.
D.
6.如图所示,物块m随转筒一起以角速度做匀速圆周运动,如下描述正确的是( )
A.物块受到重力、弹力、摩擦力和向心力的作用
B.若角速度增大而且物块仍然随转筒一起做匀速圆周运动,那么物块所受弹力增大
C.若角速度增大而且物块仍然随转筒一起做匀速圆周运动,物块所受摩擦力增大
D.若角速度增大而且物块仍然随转筒一起做匀速圆周运动,物块所受摩擦力不变
7.如图甲所示是一种利用霍尔效应传感器测量运动速率的自行车速度计。车轮每转一周,安装在自行车前轮上的一块磁铁就靠近霍尔传感器一次,产生一次电压脉冲。图乙为某次骑行中记录的脉冲电压U与时间t的图象。已知自行车车轮的半径为33cm,磁铁与轮轴的距离为车轮半径的0.75倍,则该自行车( )
A.车轮边缘与磁铁的线速度大小相等
B.在1.0s~1.4s内,速率几乎不变
C.在1.4s~2.2s内做减速运动
D.在1.2s时的速率约为10m/s
8.如图所示,水平转台上有一个质量为m的物块,用长为L的细线将物块连接在转轴上,细线与竖直转轴的夹角为θ,此时细线中张力为零,物块与转台间的动摩擦因数为μ(),最大静摩擦力等于滑动摩擦力,物块随转台由静止开始缓慢加速转动,则下列说法正确的是( )
A.转台一开始转动,细线立即绷直对物块施加拉力
B.当细线中出现拉力时,转台对物块做的功为
C.当物体的角速度为时,转台对物块的支持力为零
D.当转台对物块的支持力刚好为零时,转台对物块做的功为
9.有关圆周运动的基本模型,下列说法正确的是( )
A.如图a,汽车通过拱桥的最高点处于超重状态
B.如图b所示是一圆锥摆,增大θ,若保持圆锥的高不变,则圆锥摆的角速度不变
C.如图c,同一小球在光滑而固定的圆锥筒内的A、B位置先后分别做匀速圆周运动,则在A、B两位置小球的角速度及所受筒壁的支持力大小相等
D.火车转弯超过规定速度行驶时,外轨对火车轮缘会有挤压作用
10.如图所示,竖直平面内固定有一个半径为R的光滑圆环形细管,现给小球(直径略小于管内径)一个初速度,使小球在管内做圆周运动,小球通过最高点时的速度为v,已知重力加速度为g , 则下列叙述中正确的是( )
A.v的极小值为
B.v由零逐渐增大的过程中,轨道对球的弹力先减小再增大
C.当v由值逐渐增大的过程中,轨道对小球的弹力也逐渐增大
D.当v由值逐渐减小的过程中,轨道对小球的弹力也逐渐减小
11.某探究小组用能够显示并调节转动频率的小电动机验证匀速圆周运动的向心力关系式。
(1)如图所示,把转动频率可调的小电动机固定在支架上,转轴竖直向下,将摇臂平台置于小电动机正下方的水平桌面上
(2)在转动轴正下方固定一不可伸长的细线,小电动机转轴与细线连接点记为O。细线另一端穿过小铁球的球心并固定
(3)启动电动机,记录电动机的转动频率f,当小球转动稳定时,将摇臂平台向上移动,无限接近转动的小球
(4)关闭电动机,测量O点到摇臂平台的高度h
(5)改变电动机的转动频率,重复上述实验。本实验______(选填“需要”或“不需要)测量小球的质量。请你根据所记录的O点到摇臂平台的高度h和小球的直径D,重力加速度为g,若所测物理量满足g=_____,则成立。(用所测物理量符号表示)
12.一个喷漆桶能够向外喷射不同速度的油漆雾滴,,某同学决定测量雾滴的喷射速度,他采用如图1所示的装置,一个直径为d=40cm的纸带环,安放在一个可以按照不同转速转动的固定转台上,纸带环上刻有一条狭缝A,在狭缝A的正对面画一条标志线.如图1所示.在转台达到稳定转速时,向侧面同样开有狭缝B的纸盒中喷射油漆雾滴,当狭缝A转至与狭缝B正对平行时,雾滴便通过狭缝A在纸带的内侧面留下痕迹.将纸带从转台上取下来,展开平放,并与毫米刻度尺对齐,如图图2所示.
请你帮该同学完成下列任务:(只保留2位有效数字)
(1)设喷射到纸带上的油漆雾滴痕迹到标志线的距离为s,则从图2可知,其中速度最大的雾滴到标志线的距离s1=__cm;速度最小的雾滴到标志线的距离s2=______cm.
(2)如果转台转动的周期为T,则这些雾滴喷射速度范围的计算表达式为v0=_______(用字母表示)
(3)如果以纵坐标表示雾滴速度v0、横坐标表示雾滴距标志线距离的倒数,画出v0一图线,如图3所示,则可知转台转动的周期为T=________s.
13.如图所示,AB为竖直转轴,细绳AC 和BC 的结点C系一质量为m的小球,两绳能承担的最大拉力均为2mg。当AC和BC均拉直时,,。ABC能绕竖直轴AB匀速转动,因而C球在水平面内做匀速圆周运动。当小球的线速度增大时,两绳均会被拉断,求:
(1)哪根绳最先被拉断,被拉断时的线速度v1;
(2)另一根绳被拉断时的速度v2。(已知,,)
14.质量为的小球固定在长为的轻绳一端,绳子可绕O点的水平转轴在竖直平面内转动。,求:
(1)小球在最高点的最小速度;
(2)在最低点小球速度为9m/s时,绳中拉力为多大?
15.如图所示,轻杆长为3L,在杆的A、B两端分别固定质量均为m的球A和球B,杆上距球A为L处的点O装在光滑水平转动轴上,杆和球在竖直面内转动,已知球A运动到最高点时,球A的速度刚好为。求:
(1)球A在最高点时的角速度大小;
(2)杆此时对球B作用力大小和方向。
16.如图所示,装置可绕竖直轴转动,可视为质点的小球A与两细线连接后分别系于B、C两点,装置静止时细线AB水平,细线AC与竖直方向的夹角θ=37°.已知小球的质量m=1kg,细线AC 长L=1m,B点距C点的水平和竖直距离相等.(g取10m/s2,sin37o=0.6,cos37o=0.8,结果可用根式表达)
(1)若装置匀速转动的角速度为ω1,细线AB上的张力为零而细线AC与竖直方向夹角仍为37°,求角速度ω1的大小;
(2)若装置以ω2匀速转动时,细线AB刚好竖直且张力为零,求此时角速度ω2的大小;
参考答案
1.C
【解析】
【详解】
A. 与都做匀速圆周运动,它们的加速度的方向是不断变化的,不是匀变速运动,故A错误;
B. 、两物体一起做匀速圆周运动,质量相等,角速度相等,转动的半径相等,根据可知、的向心力相等,故B错误;
C.对分析,有:
对整体分析:
可知盘对的摩擦力是对摩擦力的2倍,故C正确;
D. 对整体分析有:
解得:
对分析有:
解得:
因为先滑动,可知先达到临界角速度,可知的临界角速度较小,即有:
故D错误。
2.C
【解析】
【详解】
A.由于向心力是效果力,故A错误;
B.当在最点时速度为时,杯子不受拉力的作用,当速度大于时,杯子受到拉力的作用,故B错误;
C.当在最点时的速度为,则在最高点,水靠重力提供向心力,杯底对水的作用力为零,故C正确;
D.在最高点,水靠重力和弹力的合力提供向心力,合力不为零,故D错误。
3.B
【解析】
【分析】
【详解】
AB.A、B两点属于同轴转动,则A、B角速度相等,由于
根据公式可知,A、B两点线速度大小之比为2:1,故A错误,B正确;
C.由于A、B角速度相等,由公式可知,A、B两点周期大小之比为1:1,故C错误;
D.由于A、B角速度相等,由公式可知,A、B两点向心加速度大小之比为2:1,故D错误。
故选B。
4.B
【解析】
【分析】
【详解】
A.向心力的方向始终指向圆心,是变化的,故A错误;
B.在最高点,由
周期
故B正确;
C.盒子在最低点,由
可得
F=2mg
故C错误;
D.盒子在与O点等高的右侧位置时,盒子底部对小球的支持力等于小球的重力mg,而盒子侧壁的支持力也等于mg,两者相互垂直,所以盒子对小球的作用力等于mg,根据牛顿第三定律,小球对盒子的作用力大小等于mg,故D错误。
故选B。
5.A
【解析】
【详解】
小球所受重力和杆子的作用力的合力提供向心力,受力如图所示;
根据牛顿第二定律有:
,
解得:
,
AC.,A正确C错误;
BD.求出来是的表达式,而并非的表达式,BD错误.
6.BD
【解析】
【分析】
【详解】
A.因为物块始终随圆筒做匀速圆周运动,所以物块受重力G、静摩擦力F静和筒壁的弹力FN,筒壁的弹力FN充当了物块随圆筒做匀速圆周运动的向心力,故A错误;
B.若角速度增大而且物块仍然随转筒一起做匀速圆周运动时,筒壁的弹力FN=m2r,随着角速度增大,物块所受弹力FN增大,故B正确;
CD.当角速度增大而且物块仍然随转筒一起做匀速圆周运动时,在竖直方向物块受的重力G与静摩擦力F静二力平衡,F静=G,即物块所受摩擦力不变,故C错误,D正确.
故选BD。
7.BCD
【解析】
【分析】
【详解】
A. 根据题意知车轮边缘与磁铁具有相同的角速度,由圆周运动的公式v=r知,车轮边缘的线速度大于磁铁的线速度,故A错误;
B.车轮每转一周,安装在自行车前轮上的一块磁铁就靠近霍尔传感器一次,产生一次电压脉冲,根据记录的脉冲电压U与时间t的图像知,在1.0s~1.4s内记录的脉冲电压U与时间t的时间间隔相等,所以在1.0s~1.4s内,速率几乎不变,故B正确;
C. 根据记录的脉冲电压U与时间t的图像知,在1.4s~2.2s内记录的脉冲电压U与时间t的时间间隔增大,所以该自行车在1.4s~2.2s内做减速运动,故C正确;
D.已知自行车车轮的半径为33cm,在1.0s~1.4s内车轮每转一周的时间为0.2s,则在1.2s时的速率约为
故D正确。
故选BCD。
8.BD
【解析】
【详解】
AB.转台刚开始转动,细线未绷紧,此时静摩擦力提供向心力,当转动到某一角速度ω1时,静摩擦力达到最大值,根据牛顿第二定律,有
此时物块线速度大小为
从开始运动到细线中将要出现拉力过程中,设转台对物块做的功为W,对物块由动能定理,可得
联立解得
故A错误,B正确;
CD.当转台对物块支持力恰好为零时,竖直方向
水平方向
联立解得
此时物块的线速度大小为
从开始运动到转台对物块的支持力刚好为零过程中,设转台对物块做的功为W2,对物块由动能定理,可得
联立解得
故C错误,D正确。
故选BD。
9.BD
【解析】
【详解】
A.当汽车在拱桥顶端时,根据牛顿第二定律则有
可得
根据牛顿第三定律可得汽车通过拱桥的最高点处汽车对桥顶的压力小于重力,处于失重状态,故A错误;
B.球受到重力和绳的拉力作用,二者合力提供向心力,向心力大小为
小球做圆周运动的半径为
由牛顿第二定律得
联立可得角速度
知保持圆锥摆的高度不变,则角速度不变,故B正确;
C.设支持力与竖直方向的夹角为,则支持力的大小
则有
由牛顿第二定律得
可得角速度
由于,所以可得
故C错误;
D.火车拐弯时超过规定速度行驶时,由于支持力和重力的合力不够提供向心力,会对外轨产生挤压,即外轨对轮缘会有挤压作用,故D正确;
故选BD。
10.BC
【解析】
【详解】
由题可知,v的极小值为0,选项A错误;当v的范围在0-范围内逐渐变大时,根据可知,FN逐渐减小;当v在大于范围内逐渐变大时,根据可知,FN逐渐变大; 故选项BC正确,D错误;故选BC.
11.不需要
【解析】
【分析】
【详解】
[1][2].设细线与竖宜方向的夹角为,根据实验原理可得
由几何关系得
联立以上三式解得
根据上式可知,实验中不需要测量小球的质量。
12.
【解析】
(1) 雾滴运动的路程一定,速度越大,运行的时间越短,此时转台转过的弧度越小,打在纸带上的点距离标志线的距离越小.所以其中速度最大的雾滴到标志线的距离S1=2.10cm;速度最小的雾滴到标志线的距离S2=2.90cm;
(2) 如果转台转动的周期为T,则雾滴运动的时间为,所以
(3)图象中斜率,可得T=1.6s.
【点睛】解决本题的关键知道雾滴运动的路程一定,速度越大,运行的时间越短,此时转台转过的弧度越小,打在纸带上的点距离标志线的距离越小.会根据求出雾滴运动的时间,再根据求出喷枪喷出雾滴的速度.
13.(1)BC先断,;(2)
【解析】
【分析】
【详解】
(1)当绳子拉直时,线速度再增大时,不变,而增大,所以BC绳先断,当时,根据向心力公式得
解得
(2)当BC线断后,小球线速度继续增大,当时,AC也断。设此时AC线与竖直方向夹角,则有
代入数据解得
,
14.(1)3m/s;(2)20N
【解析】
【分析】
【详解】
(1)小球在最高点只受重力时,速度最小,有
解得
(2)在最低点拉力和重力合力提供向心力,有
解得
15.(1) ;(2)3mg;竖直向上
【解析】
【分析】
【详解】
(1)根据可得球A在最高点时的角速度大小
(2)由于A、B两球共轴转动,此时有
对杆B受力分析,根据牛顿第二定律得
解得
方向竖直向上
16.(1);(2).
【解析】
【分析】
【详解】
(1)细线AB上张力恰为零时,小球所受合外力为mgtan37°,应用牛顿第二定律可得:mgtan37°=mω12Lsin37° 解得:
(2)装置静止时细线AB水平,细线AC与竖直方向的夹角θ=37°,B点距C点的水平和竖直距离相等,所以,B点到OO′的距离为d=Lcos37°=0.8m;若装置以ω2匀速转动时,细线AB刚好竖直且张力为零,则细线与OO′之间的夹角为θ′,由几何关系得: ,则有:θ′=53° 应用牛顿第二定律可得mgtanθ′=mω22Lsinθ′ 解得: .
