2017--2019年4套广东省普通高中学业水平考试数学(Word版含答案,不全)
文档属性
| 名称 | 2017--2019年4套广东省普通高中学业水平考试数学(Word版含答案,不全) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-05 18:14:25 | ||
图片预览




文档简介
2017年----2019年4套广东省普通高中
学业水平考试数学
2019年12月广东省普通高中学业水平考试数学
一、选择题(每小题4分)
1、已知集合,,则=( )
A.M B.N C. D.
2、设i是虚数单位,则复数( )
A.-1+i B. 1+i C. -1-i D. 1-i
3、某次歌唱比赛中,7位评委为某选手打出的分数分别为83,91,91,94,94,95,96,去掉一个最高分和一个最低分后,所剩数据的平均数为( )
A.94 B. 93 C.92 D. 91
4、直线的斜率是( )
A. B. C.2 D.-2
5、下列函数为偶函数的是( )
A. B. C. D.
6、若且,则是( )
A.第一象限角 B. 第二象限角 C. 第三象限角 D. 第四象限角
7、函数的定义域是( )
A. B. C. D.
8、在等差数列中,若,,则=( )
A.-20 B. -5 C. 0 D. 5
9、已知函数,设,则=( )
A. 2 B. C. D.
10、已满足约束条件,则的最小值是( )
A. -2 B. -3 C. -5 D. -6
11、设,,,则( )
A. B. C. D.
12、直线被圆截得的弦长为( )
A. B. 2 C. D. 1
13、已知命题,,则为( )
A. , B. ,
C. , D. ,
14、一个棱长为2的正方体,其顶点均在同一球的球面上,则该球的表面积是( )
(参考公式:球的表面积公式为,其中R是球的半径)
A. 3π B. 4π C. 8π D. 12π
15、的内角A,B,C的对边分别为a,b,c.已知,,且的面积为2,则( )
A. B. C. D.
二、填空题(每小题4分)
16、设向量,,若,则= 。
17、设等比数列的前n项和为,已知,,则= 。
18、从4张分别写有数字1,2,3,4的卡片中随机抽取2张,则所取2张卡片上的数字之积为奇数的概率是 。
19、设椭圆的两个焦点分别为,,过作椭圆长轴的垂线交椭圆于A,B两点,若为等边三角形,则该椭圆的离心率为 。
三、解答题(每小题12分)
20、已知函数,
(1)求函数的最小正周期和最大值;
(2)若满足,求的值。
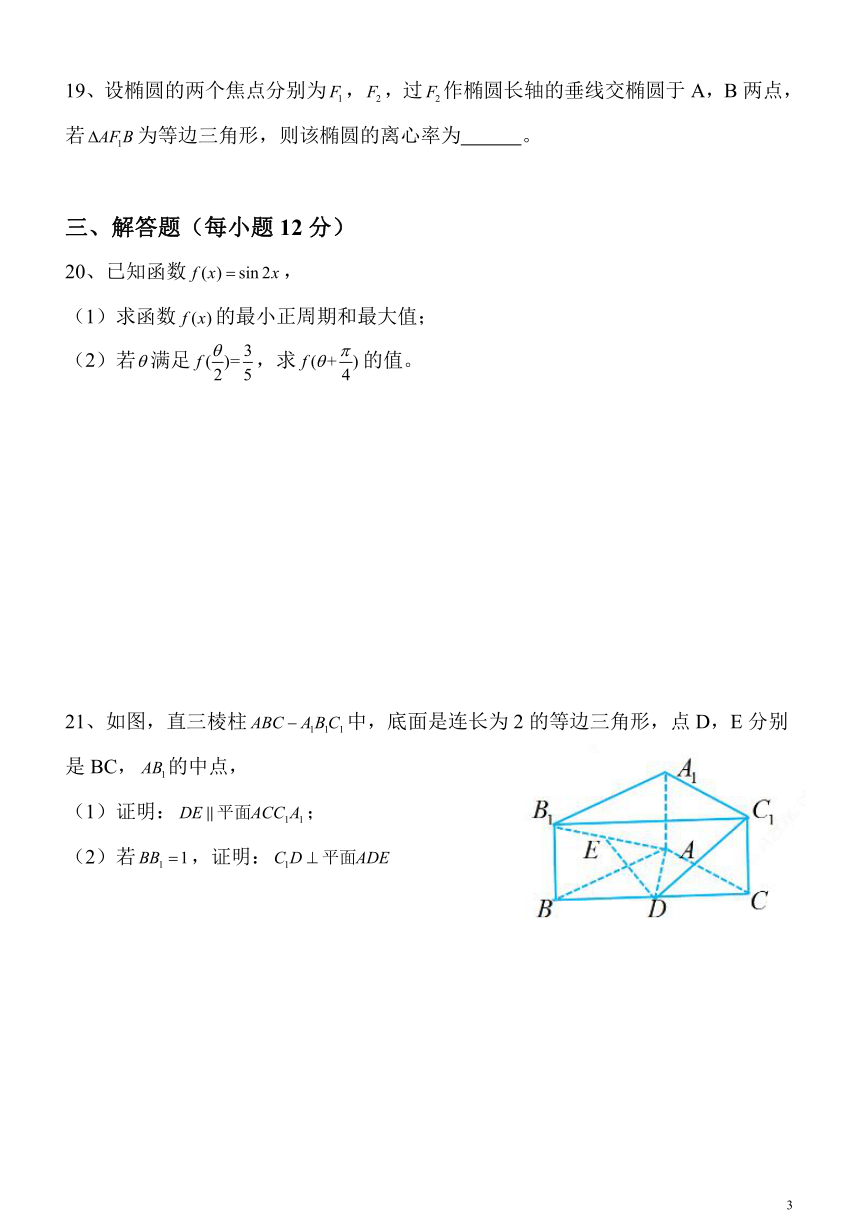
21、如图,直三棱柱中,底面是连长为2的等边三角形,点D,E分别是BC,的中点,
(1)证明:;
(2)若,证明:
1---15CABAB BDCAC DBDDB
2019年1月广东省普通高中学业水平考试
数 学
选择题:本大题共15小题,每小题4分,满分60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,则 ( )
A.{0,2} B.{-2,4 } C.[0,2] D.{-2,0,2,4}
【答案】D
2.设为虚数单位,则复数( )
A. B. C. D.
【答案】B
3.函数的定义域为( )
A. B. C. D.
【答案】A
4.已知向量,则( )
A.1 B. C.5 D. 25
【答案】C
5.直线的斜率是( )
A. B. C. D.
【答案】B
6.不等式的解集为( )
A. B. C. D.
【答案】D
7.已知,则( )
A. B. C. D.
【答案】D
8.某地区连续六天的最低气温(单位:)为:9,8,7,6,5,7,则该六天最低气温的平均数和方差分别为( )
A. B . C. D.
【答案】A
9.如图1,长方体中,,,则( )
A. 1 B. C. 2 D.
【答案】B
10.命题“”的否定是( )
A. B.
C. D.
【答案】A
11.设满足约束条件,则的最大值为( )
A. – 5 B. – 3 C. 1 D. 4
【答案】C
12.已知圆与轴相切于点,半径为5,则圆的标准方程是( )
A. B.
C.
D.
【答案】D
13.如图2,中,,用表示,正确的是( )
A. B. C. D.
【答案】C
14.若数列的通项,设,则数列的前7项和为( )
A. 14 B. 24 C. 26 D. 28
【答案】C
15.已知椭圆的长轴为,为椭圆的下顶点,设直线的斜率分别为,且,则该椭圆的离心率为( )
A. B. C. D.
【答案】B
二、填空题:本大题共4小题,每小题4分,满分16分.
16.已知角的顶点与坐标原点重合,始边与轴的非负半轴重合,终边经过点,则 .
【答案】
17.在等比数列中,,则 .
【答案】8
18.袋中装有五个除颜色外完全相同的球,其中2个白球,3个黑球,从中任取两球,则取出的两球颜色相同的概率是 .
【答案】
19.已知函数是定义在上的奇函数,当时,,则当时, .
【答案】
三、解答题:本大题共2小题,每小题12分,满分24分,解答须写出文字说明、证明过程和演算步骤.
20.的内角A,B,C的对边分别为,已知.
(1)求的面积;
(2)若,则的值.
【答案】
(1);
(2),
。
21.如图3,三棱锥中,
,是的中点,点在线段上.
(1)证明:;
(2)若,求四棱锥的体积.
(参考公式:锥体的体积公式为,其中是底面积,
是高.)
【答案】
(1)
又。
(2),
为梯形,又,为直角梯形,
又是的中点,的中点,又,
。
2018年1月广东省普通高中学业水平考试
数 学
一、选择题(本大题共15小题,每小题4分,满分60分)
1.已知集合 则( )
A.{0,1,2} B.{-1,0,1} C.M D.N
2.对任意的正实数x,y,下列等式不成立的是( )
A. B. C. D.
3.已知函数设则 ( )
A. -2 B.-1 C. D.0
4.设i是虚数单位,x是实数,若复数的虚部为2,则x=( )
A.4 B.2 C. -2 D.-4
5.设实数a为常数,则函数存在零点的充分必要条件是( )
A. B. a>1 C. D.
6.已知向量则下列结论正确的是( )
A. B. C. D.
7.某校高一(1)班有男、女学生共50人,其中男生20人,用分层抽样的方法,从该班学生中随机选取15人参加某项活动,则应选取的男、女生人数分别是( )
A. 6和9 B.9和6 C. 7和8 D. 8和7
8.如图1所示,一个空间几何体的正(主)视图和侧(左)视图都是矩形,俯视图是正方形,则该几何体的体积为( )
A. 1
B. 2
C. 4
D. 8
9.若实数x,y满足则的最小值为( )
A.0 B. -1 C. D. -2
10. 如图2所示,O是平行四边形ABCD的两条对角线的交点,则下列等式正确的是( )
A.
B.
C.
D.
11设的内角A,B,C的对边分别为a,b,c,若则C=( )
A. B. C. D.
12.已知函数则的最大值和最小正周期分别为( )
A. B. C. D.
13.设点P是椭圆上的一点,和是该椭圆的两个焦点,若,则( )
A.4 B. 8 C. D.
14.设函数f (x)是定义在R上的减函数,且f (x)为奇函数,若则下列结论不正确的是( )
A. B. C. D.
15.已知数列的前n项和,则( )
A. B. C. D.
二、填空题(本大题共4小题,每小题4分,满分16分.)
16.双曲线的离心率为
17. 若且则
18.笔筒中放有2支黑色和1支红色共3支签字笔,先从笔筒中随机取出一支笔,使用后放回笔筒,第二次再从笔筒中随机取出一支笔使用,则两次使用的都是黑色笔的概率为
19.圆心为两直线和的交点,且与直线相切的圆的标准方程是
三、解答题(本大题共2小题,每小题12分,满分24分.)
20.若等差数列满足且
(1)求的通项公式;
(2)设数列满足求的前n项和
21.如图3所示,在三棱锥P-ABC中,平面ABC, 为BC的中点,DE垂直平分PC,且DE分别交AC,PC于点D,E.
(1)证明: ;
(2) 证明:
一、选择题:本大题共15小题. 每小题4分,满分60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
B
B
C
D
C
B
A
C
D
D
A
A
B
D
C
二、填空题:本大题共4小题,每小题4分,满分16分.
15、
16、
解答题:本大题共2小题. 每小题12分,满分24分. 解答须写出文字说明、证明过程和演算步骤.
20、解:(1)设等差数列的公差为.
数列的通项公式为.
由(1)知,
又适合上式
数列是首项为,公差为的等差数列.
解:(1)证明:垂直平分 为的中点
又为的中点 为的中位线
又
证明:连接
,为的中点
垂直平分
又,
又
又,
又
2017年1月广东省普通高中学业水平考试
数 学
选择题:本大题共15小题,每小题4分,满分60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,则
A.{0,1,2,3,4} B.{0,3}
C.{0,4} D.{0}
答案:B
2.函数的定义域是
A. B.
C. D.
答案:C
3.设i为虚数单位,则复数
A.1+i B.1-i
C.-1+i D. -1-i
答案:D
4.命题甲:球体的半径为1cm,命题乙:球体的体积为,则甲是乙的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D. 既不充分也不必要条件
答案:C
5.已知直线过点A(1,2)且与直线垂直,则直线的方程是
A. B.
C. D.
答案:B
6.定点在坐标原点,准线为x=-2的抛物线的标准方程是
A. B.
C. D.
答案:A
7.已知三点A(-3,3),B(0,1)和C(1,0),则
A.5 B.4
C. D.
答案:A
8. 已知角的顶点为左边原点,始边为轴的正半轴,终边过点,则下列等式不正确的是
A. B .
C. D.
答案:D
9.下列不等式恒成立的是
A. B.
C. D.
答案:D
10.已知数列满足,且,则的前n项和
A. B.
C. D.
答案:B
11.已知实数满足,则的最大值为
A.3 B.5
C.9 D.10
答案:C
12.已知点和点,则以线段AB为直径的圆的标准方程是
A. B.
C. D.
答案:D
13.下列不等式一定成立的是
A. B.
C. D.
答案:
B
14.已知是定义在R上的偶函数,且当时,,则当时,
A. B.
C. D.
答案:A
15.已知样本的平均数为4,方差为3,则的平均数和方差分别为
A.4和3 B. 4和9
C. 10和3 D. 10和9
答案:C
二、填空题:本大题共4小题,每小题4分,满分16分.
16.已知,且成等比数列,则 5 .
17.已知函数的最小正周期是 .
18.从1,2,3,4,这四个数字中任意选取两个不同的数字,将它们组成一个两位数,该两位数小于20的概率是 .
19.中心在坐标原点的椭圆,其离心率为,两个焦点和在轴上,P为该椭圆上的任意一点,若,则此椭圆的标准方程是 .
三、解答题:本大题共2小题,每小题12分,满分24分,解答须写出文字说明、证明过程和演算步骤.
20.的内角A,B,C的对边分别为,已知.
(1)证明:为等腰三角形;
(2)若,求的值.
21.如图,在四棱锥中,
,E是PC的中点.
(1)证明:;
(2)求三棱锥的体积;
(3)证明:
PAGE
5
同课章节目录
