人教版五年级下册数学教材习题课件-第9单元 总复习(39页PPT)
文档属性
| 名称 | 人教版五年级下册数学教材习题课件-第9单元 总复习(39页PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-04 20:34:47 | ||
图片预览








文档简介
(共39张PPT)
第9单元·P116~117总复习
1.(1)“因数与倍数”单元最基本的概念是什么?请写在下面的方框中,并举例说明。
因数、倍数、奇数、偶数、质数、合数
举例略。
1.(2)你能从基本概念出发,把有关的知识整理成一个图吗?
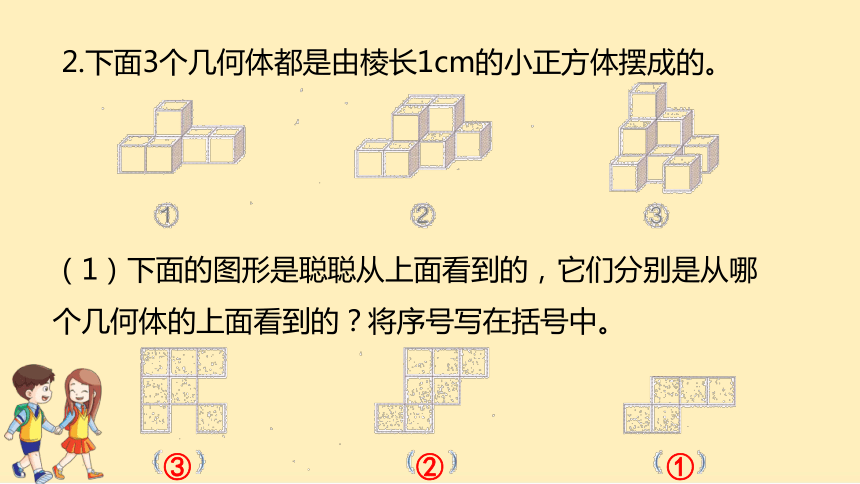
2.下面3个几何体都是由棱长1cm的小正方体摆成的。
(1)下面的图形是聪聪从上面看到的,它们分别是从哪个几何体的上面看到的?将序号写在括号中。
③
②
①
(2)①、②、③的体积分别是多少?①的体积是③的体积的几分之几?
6 cm3 10 cm3 11 cm3
(3)如果要把①、②、③分别继续补搭成一个大正方体,每个几何体至少还需要多少个小正方体?
(4)你还能提出其他数学问题并解答吗?
略
58 54 16
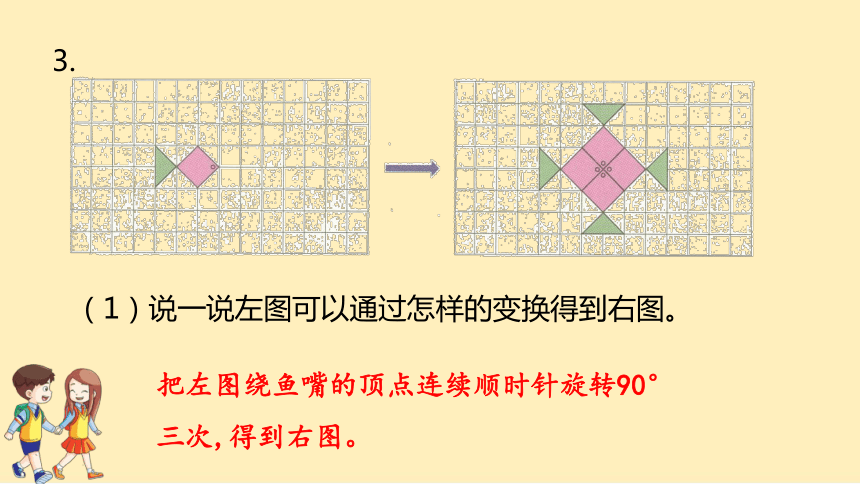
3.
把左图绕鱼嘴的顶点连续顺时针旋转90°三次,得到右图。
(1)说一说左图可以通过怎样的变换得到右图。
(2)右图中绿色部分占整个图案的几分之几?红色部分占整个图案的几分之几?红色部分比绿色部分多占整个图案的几分之几?
略
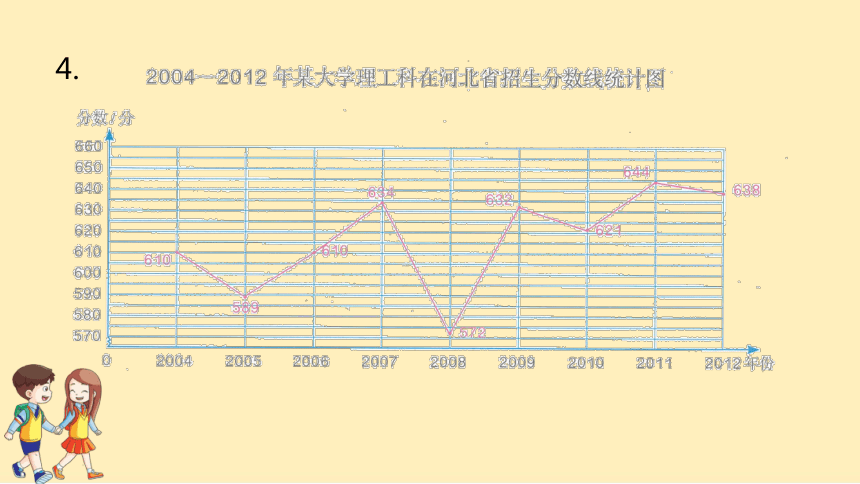
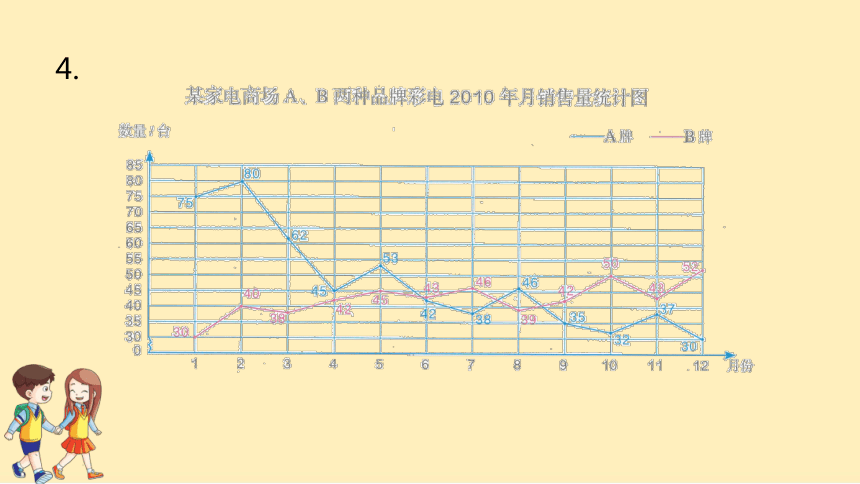
4.
4.
4.(1)观察这两个折线统计图所表示的数据,说一说折线统计图适合表示数据的什么情况。
折线统计图不仅可以表示数量的多少,还能表示数据的增减变化情况。
4.(2)说一说绘制复式折线统计图时应该注意什么。
(3)如果你是高考生或者市场经理,你能从统计图中得到哪些信息?这些信息对你有什么帮助?
绘制复式折线统计图时,一定要用不同的图例把两组数据区分开,表示数量的单位长度要相等,横轴上表示时间或其他名称的间隔要相等,在相应的点旁标出数量。
略
第9单元·P118~121练习二十八
1.下面的数,哪些是2的倍数?哪些是3的倍数?哪些是5的倍数?哪些是质数?哪些是合数?哪些是奇数?哪些是偶数?说一说你是怎样判断的。
2的倍数:56 204 630 22 78
56 79 87 195 204 630 22 31 57 65 78 83
3的倍数:87 195 204 630 57 78
5的倍数:195 630 65
质数:79 31 83
合数:56 87 195 204 630 22 57 65 78
1.下面的数,哪些是2的倍数?哪些是3的倍数?哪些是5的倍数?哪些是质数?哪些是合数?哪些是奇数?哪些是偶数?说一说你是怎样判断的。
奇数:79 87 195 31 57 65 83
56 79 87 195 204 630 22 31 57 65 78 83
偶数:56 204 630 22 78
2.下面的说法正确吗?正确的画“√”,错误的画“×”。
(1)所有的偶数都是合数。( )
(2)两个不同的质数的公因数只有1。( )
(3)一个数的因数一定比它的倍数小。( )
(4)两个数的乘积一定是它们的公倍数。( )
(5)最小的质数是1。( )
×
√
×
√
×
3.找出下面每组数的最大公因数和最小公倍数,以其中一组为例,说一说你是怎样找的。
4和5 6和16 15和20 10和8 3和9
4和5的最大公因数是1,最小公倍数是20。
6和16的最大公因数是2,最小公倍数是48。
15和20的最大公因数是5,最小公倍数是60。
10和8的最大公因数是2,最小公倍数是40。
3和9的最大公因数是3,最小公倍数是9。
4.食品店有70多个松花蛋。如果把它装进4个一排的蛋托中,正好装完;如果把它装进6个一排的蛋托中,也正好装完。你能求出有多少个松花蛋吗?
72个
5.(1)把4m长的绳子平均剪成5段,每段长
m,每段绳子是全长的 。
4
5
1
5
(2)1985年第二次大熊猫调查结果显示,全国共有1114只野生大熊猫。2000年开始的第三次大熊猫调查,最终确认我国共有1596只野生大熊猫,其中1206只生活在四川。第二次调查到的野生大熊猫的数量是第三次
调查数量的 ,第三次调查中生活在四川的野生大熊猫占所有野生大熊猫数量的 。
557
798
201
266
6.用直线上的点表示下面各数,估计一下哪个数最接近2。
最接近2。
1.5 2 3.7 2.8
1
3
5
4
17
8
3
5
3
5
13
10
17
8
7.先填空,再把各数按照从小到大的顺序排列。
6
2
7
( )
21
9
12
3
( )
= =
( )
( )
( )
( )
( )
( )
5÷3= =1 2=
4
5
3
2
3
4
2
(答案不唯一)
< <5÷3<2
2
7
9
12
8.下面哪些数是最简分数?把不是最简分数的化成最简分数,并说一说化简的依据。
最简分数: 其余的不是最简分数
6
8
36
16
10
21
5
7
30
45
12
25
72
6
10
21
12
25
5
7
= = = =12
36
16
30
45
6
8
3
4
9
4
72
6
2
3
+ -
- + +
9.计算下面各题。
=1
5
6
3
10
1
6
4
7
1
3
1
6
1
5
7
10
1
2
=
2
3
=
5
21
=
13
15
7- 6-( - )
9.计算下面各题。
2
3
- +
7
8
7
9
5
3
3
4
3
4
2
5
=
1
8
=
13
9
=
16
3
=5
13
20
计算时要注意通分,计算结果要化成最简分数。
10.中国煤炭资源的种类较多,具体构成如右图。
(1)褐煤占煤炭总量的几分之几?
(2)你还能提出其他数学问题并解答吗?
1- - =
3
4
3
25
13
100
(答案不唯一)烟煤比无烟煤多占煤炭总量的几分之几
- =
3
4
3
25
63
100
11.填写下表。
S长方体=(ab+ah+bh)×2
V长方体=abh
S正方体=6a2
V正方体=a3
12.(1)举例说明1cm3、 1dm3、 1m3各有多大,1L、1mL的水大约有多少。
(2)1m3= dm3 700dm3= m3
81cm3= mL 1L= dm3
2.3dm3= cm3 560mL= L
1000
0.7
81
1
2300
0.56
13.一块长方形铁皮(如右图),从四个角各切掉一个边长为5cm的正方形,然后做成盒子。这个盒子用了多少铁皮?它的容积有多少?
30-5×2=20(cm)
25-5×2=15(cm)
(20×5+15×5)×2+20×15=650(cm2)
20×15×5=1500(cm3)
14.一个长方体的玻璃缸,长8dm,宽6dm,高4dm,水深2.8dm。如果投入一块棱长为4dm的正方体铁块(如右图),缸里的水溢出多少升?
4-2.8=1.2(dm)
4×4×4-8×6×1.2=6.4(dm3)
6.4 dm3=6.4 L
15.用4个 摆一摆。
(1)如果左侧看到的形状是 ,这4个小正方体可能是怎样摆放的?
(答案不唯一)
15.用4个 摆一摆。
(2)请你再给出从另一个方向看到的形状,让同桌猜一猜4个 是怎样摆放的。
(答案不唯一)
16.画出“风筝”旋转90°后的图形(只画出轮廓线)。
说说怎样旋转并画出略
17.我国2000-2010年学龄儿童人数和入学人数统计图如下。
(1)哪年学龄儿童最多?哪年最少?
(2)哪年没上学的学龄儿童最多?哪年最少?
(3)你还能发现什么?
2000年学龄儿童最多,2010年最少。
2002年没上学的学龄儿童最多,2010年最少。
18.某地区1990-2010年年人均支出和年人均食品支出如下图所示。
(1)每年年人均食品支出各占年人均支出的几分之几?
1990年:400÷800= =
400
800
1
2
(2)比较这几个分数的大小,你能发现什么?
1995年:900÷2000= =
900
2000
9
20
2000年:1600÷4000=
2
5
2005年:2324÷4593=
2324
4593
2010年:2831÷5612=
2831
5612
有数字卡片 、 、 、 各一张,每次取两张组成一个两位数,可以组成多少个偶数?
根据偶数的概念,只有把2和4这两张卡片放在个位才能符合要求。当2放在个位上时,能组成3个偶数,当4放在个位上时,也能组成3个偶数,故一共可以组成6个偶数,分别是:12,32,42,14,24,34。
1
2
3
4
再
见
第9单元·P116~117总复习
1.(1)“因数与倍数”单元最基本的概念是什么?请写在下面的方框中,并举例说明。
因数、倍数、奇数、偶数、质数、合数
举例略。
1.(2)你能从基本概念出发,把有关的知识整理成一个图吗?
2.下面3个几何体都是由棱长1cm的小正方体摆成的。
(1)下面的图形是聪聪从上面看到的,它们分别是从哪个几何体的上面看到的?将序号写在括号中。
③
②
①
(2)①、②、③的体积分别是多少?①的体积是③的体积的几分之几?
6 cm3 10 cm3 11 cm3
(3)如果要把①、②、③分别继续补搭成一个大正方体,每个几何体至少还需要多少个小正方体?
(4)你还能提出其他数学问题并解答吗?
略
58 54 16
3.
把左图绕鱼嘴的顶点连续顺时针旋转90°三次,得到右图。
(1)说一说左图可以通过怎样的变换得到右图。
(2)右图中绿色部分占整个图案的几分之几?红色部分占整个图案的几分之几?红色部分比绿色部分多占整个图案的几分之几?
略
4.
4.
4.(1)观察这两个折线统计图所表示的数据,说一说折线统计图适合表示数据的什么情况。
折线统计图不仅可以表示数量的多少,还能表示数据的增减变化情况。
4.(2)说一说绘制复式折线统计图时应该注意什么。
(3)如果你是高考生或者市场经理,你能从统计图中得到哪些信息?这些信息对你有什么帮助?
绘制复式折线统计图时,一定要用不同的图例把两组数据区分开,表示数量的单位长度要相等,横轴上表示时间或其他名称的间隔要相等,在相应的点旁标出数量。
略
第9单元·P118~121练习二十八
1.下面的数,哪些是2的倍数?哪些是3的倍数?哪些是5的倍数?哪些是质数?哪些是合数?哪些是奇数?哪些是偶数?说一说你是怎样判断的。
2的倍数:56 204 630 22 78
56 79 87 195 204 630 22 31 57 65 78 83
3的倍数:87 195 204 630 57 78
5的倍数:195 630 65
质数:79 31 83
合数:56 87 195 204 630 22 57 65 78
1.下面的数,哪些是2的倍数?哪些是3的倍数?哪些是5的倍数?哪些是质数?哪些是合数?哪些是奇数?哪些是偶数?说一说你是怎样判断的。
奇数:79 87 195 31 57 65 83
56 79 87 195 204 630 22 31 57 65 78 83
偶数:56 204 630 22 78
2.下面的说法正确吗?正确的画“√”,错误的画“×”。
(1)所有的偶数都是合数。( )
(2)两个不同的质数的公因数只有1。( )
(3)一个数的因数一定比它的倍数小。( )
(4)两个数的乘积一定是它们的公倍数。( )
(5)最小的质数是1。( )
×
√
×
√
×
3.找出下面每组数的最大公因数和最小公倍数,以其中一组为例,说一说你是怎样找的。
4和5 6和16 15和20 10和8 3和9
4和5的最大公因数是1,最小公倍数是20。
6和16的最大公因数是2,最小公倍数是48。
15和20的最大公因数是5,最小公倍数是60。
10和8的最大公因数是2,最小公倍数是40。
3和9的最大公因数是3,最小公倍数是9。
4.食品店有70多个松花蛋。如果把它装进4个一排的蛋托中,正好装完;如果把它装进6个一排的蛋托中,也正好装完。你能求出有多少个松花蛋吗?
72个
5.(1)把4m长的绳子平均剪成5段,每段长
m,每段绳子是全长的 。
4
5
1
5
(2)1985年第二次大熊猫调查结果显示,全国共有1114只野生大熊猫。2000年开始的第三次大熊猫调查,最终确认我国共有1596只野生大熊猫,其中1206只生活在四川。第二次调查到的野生大熊猫的数量是第三次
调查数量的 ,第三次调查中生活在四川的野生大熊猫占所有野生大熊猫数量的 。
557
798
201
266
6.用直线上的点表示下面各数,估计一下哪个数最接近2。
最接近2。
1.5 2 3.7 2.8
1
3
5
4
17
8
3
5
3
5
13
10
17
8
7.先填空,再把各数按照从小到大的顺序排列。
6
2
7
( )
21
9
12
3
( )
= =
( )
( )
( )
( )
( )
( )
5÷3= =1 2=
4
5
3
2
3
4
2
(答案不唯一)
< <5÷3<2
2
7
9
12
8.下面哪些数是最简分数?把不是最简分数的化成最简分数,并说一说化简的依据。
最简分数: 其余的不是最简分数
6
8
36
16
10
21
5
7
30
45
12
25
72
6
10
21
12
25
5
7
= = = =12
36
16
30
45
6
8
3
4
9
4
72
6
2
3
+ -
- + +
9.计算下面各题。
=1
5
6
3
10
1
6
4
7
1
3
1
6
1
5
7
10
1
2
=
2
3
=
5
21
=
13
15
7- 6-( - )
9.计算下面各题。
2
3
- +
7
8
7
9
5
3
3
4
3
4
2
5
=
1
8
=
13
9
=
16
3
=5
13
20
计算时要注意通分,计算结果要化成最简分数。
10.中国煤炭资源的种类较多,具体构成如右图。
(1)褐煤占煤炭总量的几分之几?
(2)你还能提出其他数学问题并解答吗?
1- - =
3
4
3
25
13
100
(答案不唯一)烟煤比无烟煤多占煤炭总量的几分之几
- =
3
4
3
25
63
100
11.填写下表。
S长方体=(ab+ah+bh)×2
V长方体=abh
S正方体=6a2
V正方体=a3
12.(1)举例说明1cm3、 1dm3、 1m3各有多大,1L、1mL的水大约有多少。
(2)1m3= dm3 700dm3= m3
81cm3= mL 1L= dm3
2.3dm3= cm3 560mL= L
1000
0.7
81
1
2300
0.56
13.一块长方形铁皮(如右图),从四个角各切掉一个边长为5cm的正方形,然后做成盒子。这个盒子用了多少铁皮?它的容积有多少?
30-5×2=20(cm)
25-5×2=15(cm)
(20×5+15×5)×2+20×15=650(cm2)
20×15×5=1500(cm3)
14.一个长方体的玻璃缸,长8dm,宽6dm,高4dm,水深2.8dm。如果投入一块棱长为4dm的正方体铁块(如右图),缸里的水溢出多少升?
4-2.8=1.2(dm)
4×4×4-8×6×1.2=6.4(dm3)
6.4 dm3=6.4 L
15.用4个 摆一摆。
(1)如果左侧看到的形状是 ,这4个小正方体可能是怎样摆放的?
(答案不唯一)
15.用4个 摆一摆。
(2)请你再给出从另一个方向看到的形状,让同桌猜一猜4个 是怎样摆放的。
(答案不唯一)
16.画出“风筝”旋转90°后的图形(只画出轮廓线)。
说说怎样旋转并画出略
17.我国2000-2010年学龄儿童人数和入学人数统计图如下。
(1)哪年学龄儿童最多?哪年最少?
(2)哪年没上学的学龄儿童最多?哪年最少?
(3)你还能发现什么?
2000年学龄儿童最多,2010年最少。
2002年没上学的学龄儿童最多,2010年最少。
18.某地区1990-2010年年人均支出和年人均食品支出如下图所示。
(1)每年年人均食品支出各占年人均支出的几分之几?
1990年:400÷800= =
400
800
1
2
(2)比较这几个分数的大小,你能发现什么?
1995年:900÷2000= =
900
2000
9
20
2000年:1600÷4000=
2
5
2005年:2324÷4593=
2324
4593
2010年:2831÷5612=
2831
5612
有数字卡片 、 、 、 各一张,每次取两张组成一个两位数,可以组成多少个偶数?
根据偶数的概念,只有把2和4这两张卡片放在个位才能符合要求。当2放在个位上时,能组成3个偶数,当4放在个位上时,也能组成3个偶数,故一共可以组成6个偶数,分别是:12,32,42,14,24,34。
1
2
3
4
再
见
