苏科版数学八年级下册第11章《反比例函数》达标测试(含详细答案)
文档属性
| 名称 | 苏科版数学八年级下册第11章《反比例函数》达标测试(含详细答案) |  | |
| 格式 | zip | ||
| 文件大小 | 260.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-04 16:21:40 | ||
图片预览

文档简介
苏科版八年级下册第11章《反比例函数》达标测试
(满分100分)
题号 一 二 三 总分
得分
姓名:___________班级:___________
一.选择题(共8小题,满分24分)
1.下列关系式中,y是x的反比例函数的是( )
A.y=5x B. C. D.y=x2﹣3
2.点M(1,3)在反比例函数y=的图象上,则k的值为( )
A.﹣1 B.3 C.﹣3 D.
3.已知函数y=(a+3)xa+1是反比例函数,则此反比例函数的图象在( )
A.第一、三象限 B.第二、四象限
C.第一、四象限 D.第二、三象限
4.若点A(x1,1)、B(x2,﹣2)、C(x3,﹣3)在反比例函数y=﹣的图象上,则x1、x2、x3的大小关系是( )
A.x1<x2<x3 B.x1<x3<x2 C.x3<x1<x2 D.x2<x1<x3
5.对于反比例函数,下列说法中不正确的是( )
A.点(﹣2,﹣1)在它的图象上
B.它的图象在第一、三象限
C.y随x的增大而减小
D.当x<0时,y随x的增大而减小
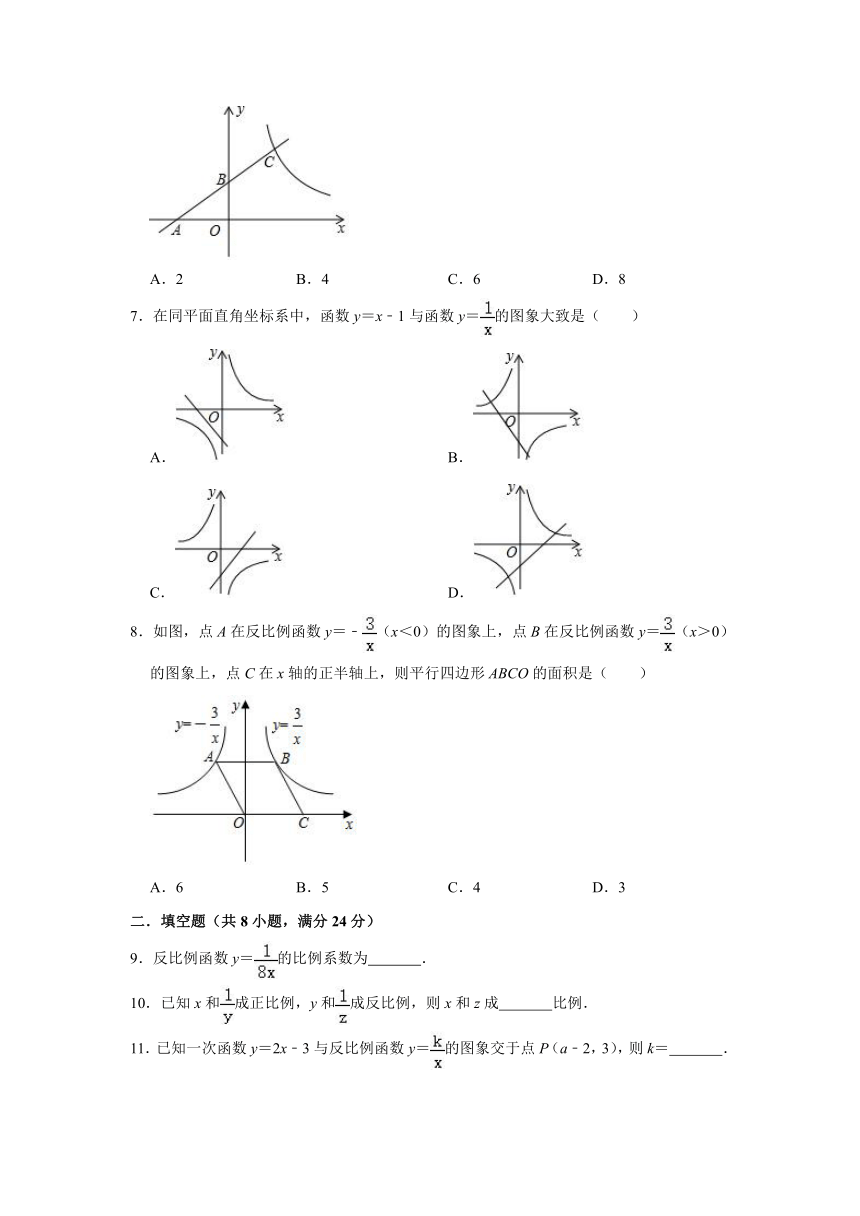
6.如图,点C在反比例函数y=(x>0)的图象上,过点C的直线x轴、y轴分别交于点A、B,且AB=BC,△AOB的面积为2,则k的值为( )
A.2 B.4 C.6 D.8
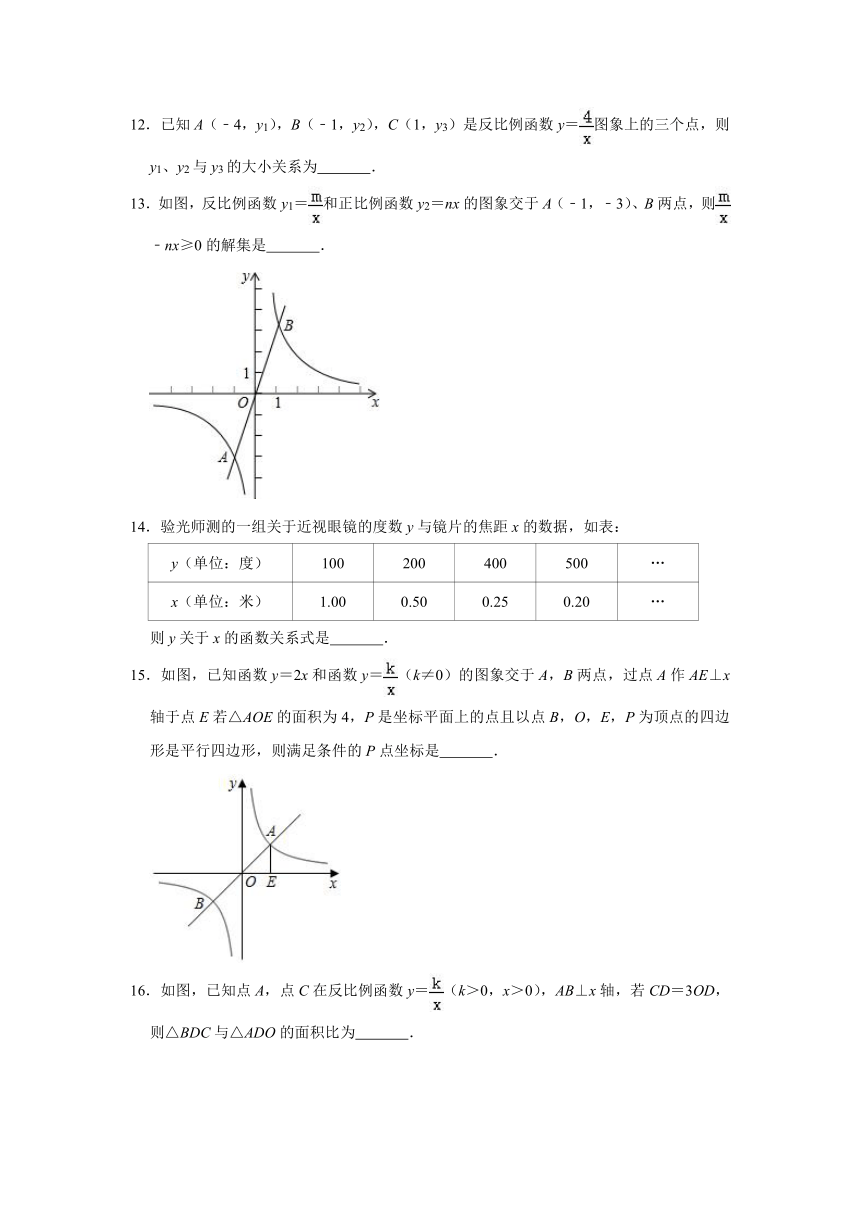
7.在同平面直角坐标系中,函数y=x﹣1与函数y=的图象大致是( )
A. B.
C. D.
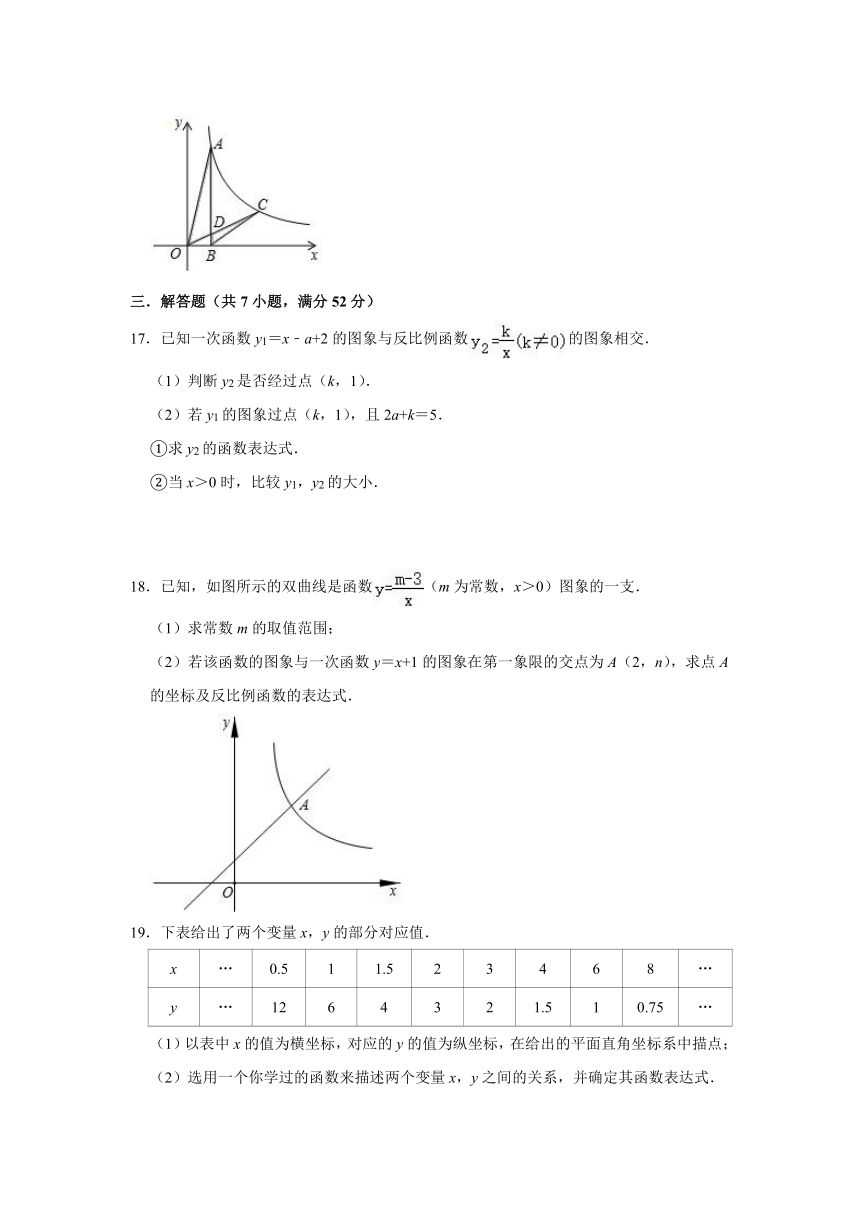
8.如图,点A在反比例函数y=﹣(x<0)的图象上,点B在反比例函数y=(x>0)的图象上,点C在x轴的正半轴上,则平行四边形ABCO的面积是( )
A.6 B.5 C.4 D.3
二.填空题(共8小题,满分24分)
9.反比例函数y=的比例系数为 .
10.已知x和成正比例,y和成反比例,则x和z成 比例.
11.已知一次函数y=2x﹣3与反比例函数y=的图象交于点P(a﹣2,3),则k= .
12.已知A(﹣4,y1),B(﹣1,y2),C(1,y3)是反比例函数y=图象上的三个点,则y1、y2与y3的大小关系为 .
13.如图,反比例函数y1=和正比例函数y2=nx的图象交于A(﹣1,﹣3)、B两点,则﹣nx≥0的解集是 .
14.验光师测的一组关于近视眼镜的度数y与镜片的焦距x的数据,如表:
y(单位:度) 100 200 400 500 …
x(单位:米) 1.00 0.50 0.25 0.20 …
则y关于x的函数关系式是 .
15.如图,已知函数y=2x和函数y=(k≠0)的图象交于A,B两点,过点A作AE⊥x轴于点E若△AOE的面积为4,P是坐标平面上的点且以点B,O,E,P为顶点的四边形是平行四边形,则满足条件的P点坐标是 .
16.如图,已知点A,点C在反比例函数y=(k>0,x>0),AB⊥x轴,若CD=3OD,则△BDC与△ADO的面积比为 .
三.解答题(共7小题,满分52分)
17.已知一次函数y1=x﹣a+2的图象与反比例函数的图象相交.
(1)判断y2是否经过点(k,1).
(2)若y1的图象过点(k,1),且2a+k=5.
①求y2的函数表达式.
②当x>0时,比较y1,y2的大小.
18.已知,如图所示的双曲线是函数(m为常数,x>0)图象的一支.
(1)求常数m的取值范围;
(2)若该函数的图象与一次函数y=x+1的图象在第一象限的交点为A(2,n),求点A的坐标及反比例函数的表达式.
19.下表给出了两个变量x,y的部分对应值.
x … 0.5 1 1.5 2 3 4 6 8 …
y … 12 6 4 3 2 1.5 1 0.75 …
(1)以表中x的值为横坐标,对应的y的值为纵坐标,在给出的平面直角坐标系中描点;
(2)选用一个你学过的函数来描述两个变量x,y之间的关系,并确定其函数表达式.
20.直线y=x+m与双曲线y=.
(1)无论m为何值,直线与双曲线都有交点,求k的取值范围;
(2)若直线y=x+m与双曲线y=的交点为A(x1,y1),B(x2,y2)(x1+x2≠0)问的值是否为定值,若是,请求出;若不是,请说明理由.
21.如图,已知一次函数y1=ax+b与反比例函数y2=的图象交于A(2,4),B(﹣4,n)两点.
(1)求反比例函数的解析式;
(2)求△AOB的面积.
22.某气球内充满了一定量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)求这一函数的解析式;
(2)当气体体积为1m3时,气压是多少?
(3)当气球内的气压大于140kPa时,气球将爆炸,为了安全起见,气体的体积应不小于多少?(精确到0.01m3)
23.如图,一次函数y=﹣x+b的图象与反比例函数y=(x>0)的图象交于点A(m,3)和B(3,n).过A作AC⊥x轴于C,交OB于E,且EB=2EO
(1)求一次函数和反比例函数解析式
(2)点P是线段AB上异于A,B的一点,过P作PD⊥x轴于D,若四边形APDC面积为S,求S的取值范围.
参考答案
一.选择题(共8小题)
1.【解答】解:选项A是正比例函数,不符合题意;
选项B可化为y=3x(x不为0),不是反比例函数,故错误;
选项C,是反比例函数,符合题意;
选项D是二次函数,不符合题意.
综上,只有C正确.
故选:C.
2.【解答】解:把x=1,y=3,代入y=得:k=3,
故选:B.
3.【解答】解:∵函数y=(a+3)xa+1是反比例函数,
∴a+1=﹣1,且a+3≠0,
∴a=﹣2,
∴a+3=1>0,
∴反比例函数的图象在第一、三象限,
故选:A.
4.【解答】解:∵反比例函数为y=y=﹣中的﹣(k2+1)<0,
∴函数图象在第二、四象限,在每个象限内,y随着x的增大而增大,
又∵A(x1,1)、B(x2,﹣2)、C(x3,﹣3)
∴x1<0,点B、C位于第四象限,
∴x2>x3>0.
∴x1<x3<x2
故选:B.
5.【解答】解:A、把点(﹣2,﹣1)代入反比例函数y=得﹣1=﹣1,本选项正确;
B、∵k=2>0,∴图象在第一、三象限,本选项正确;
C、当x>0时,y随x的增大而减小,本选项不正确;
D、当x<0时,y随x的增大而减小,本选项正确.
故选:C.
6.【解答】解:设点A的坐标为(a,0),
∵过点C的直线与x轴,y轴分别交于点A,B,且AB=BC,△AOB的面积为1,
∴点C(﹣a,),
∴点B的坐标为(0,﹣),
∴,
解得,k=8,
故选:D.
7.【解答】解:函数y=中k=1>0,故图象在第一、三象限;函数y=x﹣1的图象在第一、三、四象限,
故选:D.
8.【解答】解:过点B作BM⊥OC,垂足为M,
设点B(m,n),则OM=m,MB=ON=n,mn=3,
∵y=﹣(x<0)与y=(x>0)关于y轴对称,
∴AN=BN=2m,
∴S四边形OABC=AB?ON=2m×n=6,
故选:A.
二.填空题(共8小题)
9.【解答】解:∵y==,
∴反比例函数y=的比例系数是,
故答案为:.
10.【解答】解:由题意可列解析式y=,x=
∴x=
∴x是z的反比例函数.
故答案是:反.
11.【解答】解:∵一次函数y=2x﹣3经过点P(a﹣2,3),
∴3=2(a﹣2)﹣3,
解得a=5,
∴P(3,3),
∵点P在反比例函数y=的图象上,
∴k=3×3=9,
故答案为9.
12.【解答】解:∵y=,
∴x=﹣4时,y1=﹣1,
x=﹣1时,y2=﹣4,
x=1时,y3=4,
∴y3>y1>y2,
故答案为y3>y1>y2.
13.【解答】解:∵反比例函数y1=和正比例函数y2=nx的图象交于A(﹣1,﹣3)、B两点,
∴点B与点A关于原点对称,
∴B(1,3).
根据图象可知:﹣nx≥0的解集是x≤﹣1或0<x≤1,
故答案为x≤﹣1或0<x≤1.
14.【解答】解:根据表格数据可得近视眼镜的度数y与镜片的焦距x成反比例,
设y关于x的函数关系式是y=,
∵y=400,x=0.25,
∴400=,
解得:k=100,
∴y关于x的函数关系式是y=.
故答案为:y=.
15.【解答】解:如图,∵△AOE的面积为4,函数y=的图象过一、三象限,
∴S△AOE=?OE?AE=4,
∴OE?AE=8,
∴xy=8,
∴k=8,
∵函数y=2x和函数y=(k≠0)的图象交于A,B两点,
∴2x=,
∴x=±2,
当x=2时,y=4,当x=﹣2时,y=﹣4,
∴A、B两点的坐标是:(2,4)(﹣2,﹣4),
∵以点B、O、E、P为顶点的平行四边形共有3个,
∴满足条件的P点有3个,分别为:
P1(0,﹣4),P2(﹣4,﹣4),P3(4,4).
故答案为:(0,﹣4)或(﹣4,﹣4)或(4,4).
16.【解答】解:如图所示,过C作CE⊥x轴于E,
∵AB⊥x轴于点B,
∴S△AOB=S△COE,
∴S△AOD=S四边形BDCE,
设△BDO的面积为S,
∵CD=3OD,
∴△BDC的面积为3S,△BOC的面积为4S,
∵BD∥CE,
∴BE=3OB,
∴△BCE的面积为12S,
∴四边形BDCE的面积为12S+3S=15S,
即△AOD的面积为15S,
∴△BDC与△ADO的面积比为3:15=1:5,
故答案为:1:5.
三.解答题(共7小题)
17.【解答】解:(1)点(k,1)满足反比例函数的关系式,
因此y2经过点(k,1).
(2)①把(k,1)代入一次函数y1=x﹣a+2得,k﹣a+2=1,
又∵2a+k=5,
解得:a=2,k=1,
∴y2的函数表达式为y2=.
②由函数的图象可知:当0<x<1时,y1<y2,当x>2时,y1>y2.
18.【解答】解:(1)根据图象得m﹣3>0,解得m>3;
(2)∵点A(2,n)在一次函数y=x+1的图象上,
∴n=2+1=3,则A点的坐标为(2,3).
又∵点A在反比例函数 (m为常数,x>0)的图象上,
∴m﹣3=2×3=6,
∴反比例函数的表达式为y=.
19.【解答】解:(1)如右图所示;
(2)观察这些点的排列规律,可用反比例函数描述两个变量x、y之间的关系,
设y=,
∵当x=1时,y=6,
∴6=,得k=6,
∴函数表达式为y=.
20.【解答】解:(1)∵直线y=x+m经过第一、三象限,
∴当反比例函数图象分布在第一、三象限时,无论m为何值,直线与双曲线都有交点,
∴k的范围为k>0;
(2)的值为定值.
理由如下:
∵直线y=x+m与双曲线y=的交点为A(x1,y1),B(x2,y2),
∴点A、点B的横纵坐标满足,
∴x+m=,
整理得x2+mx﹣k=0,
∴x1+x2=﹣m,
∵y1=x1+m,x2=x2+m,
∴y1+y2=x1+x2+2m=﹣m+2m=m,
∴==﹣1.
21.【解答】解:(1)∵点A(2,4)在反比例函数y2=的图象上,
∴k=2×4=8,
∴反比例函数的解析式为y2=;
(2)将点A(2,4)、B(﹣4,﹣2)代入到y1=ax+b中,
得:
解得:,
∴一次函数的解析式为y=x+2,
令y=0,求得x=﹣2,
∴S△AOB=S△AOC+S△BOC=×2×2+2×4=6.
22.【解答】解:(1)设,
由题意知,
所以k=96,
故;
(2)当v=1m3时,;
(3)当p=140kPa时,.
所以为了安全起见,气体的体积应不少于0.69m3.
23.【解答】解:(1)∵EB=2EO,
∴OE:OB=1:3,
∵B点横坐标为3,
∴A点的横坐标为1,即m=1,
∵点A(1,3)在直线y=﹣x+b 及y=上,
∴b=4,k=3,
∴y=﹣x+4,y=;
(2)设P点坐标为(a,﹣a+4)(1<a<3),
S=(AC+PD)?CD=(3﹣a+4)(a﹣1)=﹣ (a﹣4)2+,
∵﹣<0,
∴当a<4时,S随a的增大而增大,
∵当a=1时,S=0;a=3时S=4,
∵1<a<3,
∴0<S<4.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
