人教版八年级数学下册课件:18.2.2菱形的判定 (共23张PPT)
文档属性
| 名称 | 人教版八年级数学下册课件:18.2.2菱形的判定 (共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-05 17:58:28 | ||
图片预览





文档简介
课件23张PPT。18.2.2
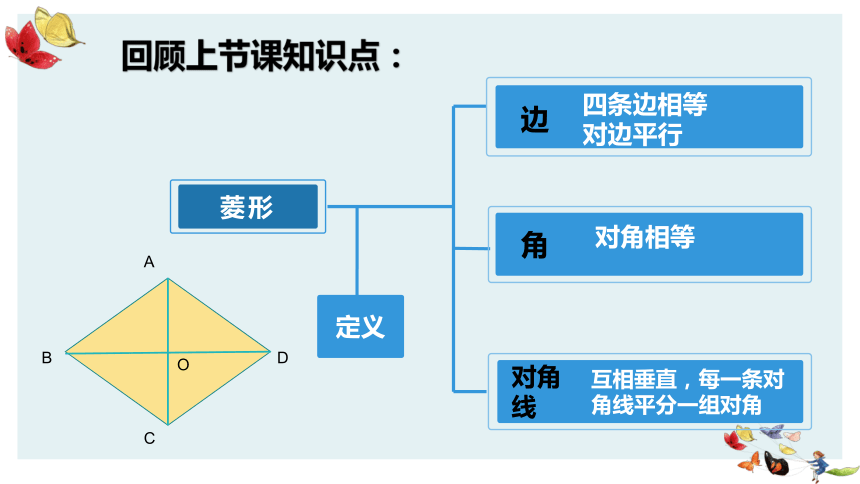
菱形的判定01学习目标02判定方法03课堂练习04课堂小结目录第一节 学习目标学习目标:1. 掌握菱形的所有判定方法2. 综合应用菱形的性质与判定第二节 菱形的判定菱形定义边角对角线四条边相等
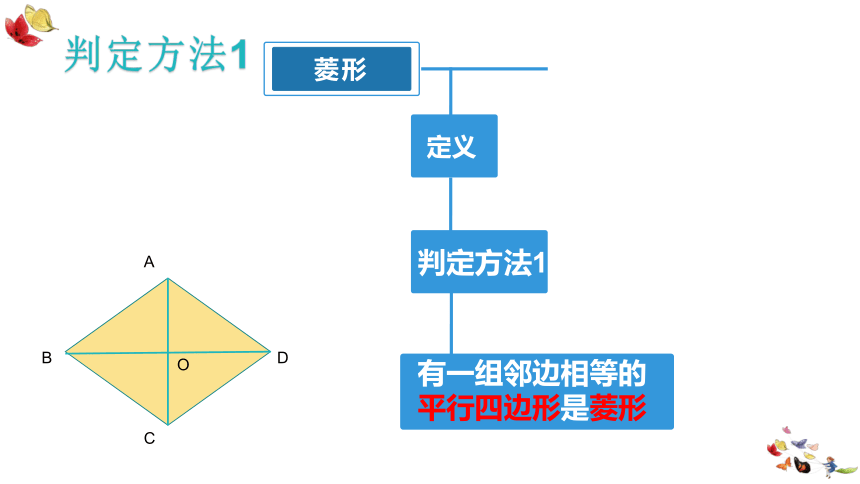
对边平行对角相等互相垂直,每一条对角线平分一组对角回顾上节课知识点:ABCDO判定方法1菱形定义互相垂直,每一条对角线平分一组对角ABCDO判定方法1有一组邻边相等的 平行四边形是菱形
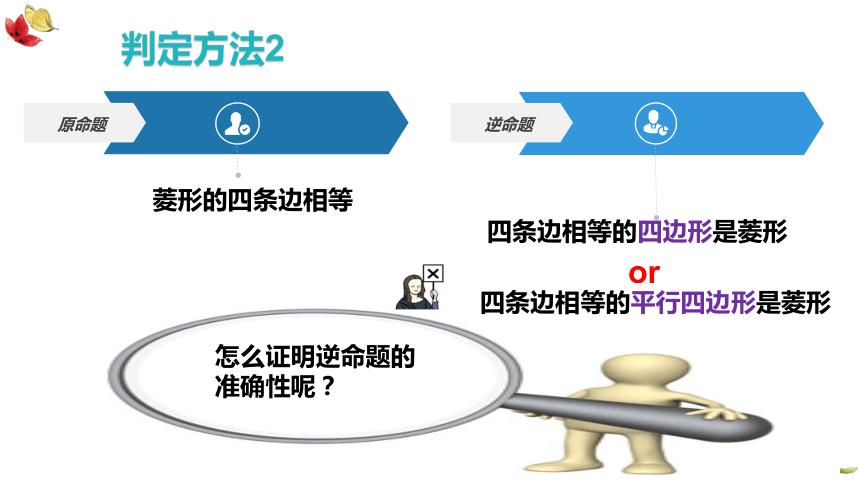
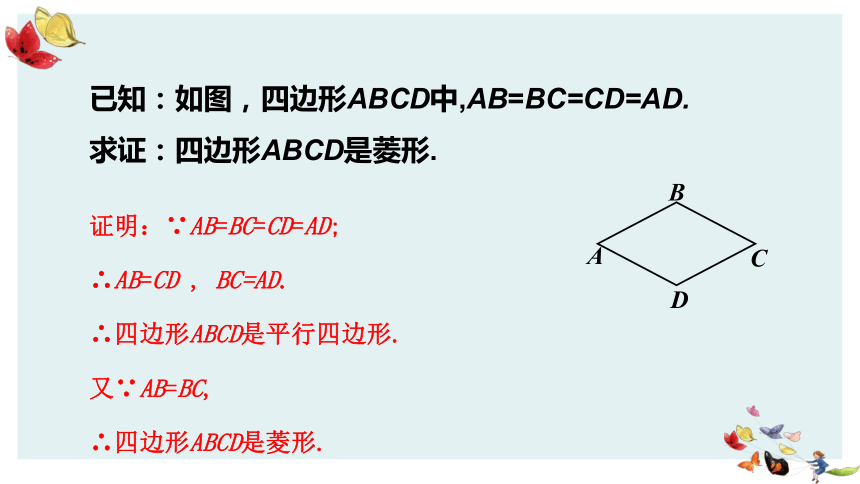
逆命题原命题菱形的四条边相等四条边相等的四边形是菱形or四条边相等的平行四边形是菱形怎么证明逆命题的准确性呢?判定方法2已知:如图,四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.证明:∵AB=BC=CD=AD;
∴AB=CD , BC=AD.
∴四边形ABCD是平行四边形.
又∵AB=BC,
∴四边形ABCD是菱形.
四条边相等的四边形是菱形符号语言:因为 AB=BC=CD=AD
所以 四边形ABCD是菱形判定方法2ABCDO逆命题原命题菱形的对角线互相垂直对角线互相垂直的平行四边形是菱形判定方法3对角线互相垂直的四边形是不是菱形?逆命题原命题菱形的对角线互相垂直对角线互相垂直的平行四边形是菱形判定方法3举反例:证明: ∵四边形ABC是平行四边形
∴OA=OC
又∵ AC ⊥ BD;
∴BA=BC
∴ ABCD是菱形
对角线互相垂直的平行四边形是菱形符号语言:因为 四边形ABCD是
平行四边形
AC⊥BD
所以 平行四边形ABCD是菱形判定方法3ABCDO第三节 课堂练习又∵四边形ABCD是平行四边形,∵ OA=4,OB=3,AB=5,证明:即AC⊥BD,∴ AB2=OA2+OB2,∴△AOB是直角三角形,∴四边形ABCD是菱形. 1. 判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直且平分的四边形是菱形;
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形;
(4) 有一条对角线平分一组对角的
平行四边形是菱形.√ ╳ ╳ √ 2. □ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是 形; (2)若AC=BD,则□ABCD是 形; (3)若∠ABC是直角,则□ABCD是 形; (4)若∠BAO=∠DAO,则□ABCD是 形。
菱菱矩矩3.下列命题中正确的是( )
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形4.下列条件中,
不能判定四边形ABCD为菱形的是( )
A.AC⊥BD,AC与BD互相平分
B.AB=BC=CD=DA
C.AB=BC,AD=CD,且AC⊥BD
D.AB=CD,AD=BC,AC⊥BD
CC3. 如图,顺次连接矩形ABCD各边的中点,得到四边形EFGH.求证:四边形EFGH是菱形.证明:因为 四边形ABCD是矩形
所以 ∠A=∠B,AD=BC
又因为 E,FG,H是各边的中点
所以 AE=BG,AF=BF
所以 △AEF≌△BGF(SAS)
所以 EF=GF
同理可得 EH=GH,EF,EH,GH=GF
所以 EF=GF=GH=EH
所以 四边形EFGH是菱形
第四节 课堂小结课堂小结一组邻边相等对角线互相垂直四条边相等五种判定方法菱形的判定方法:感谢观看
对边平行对角相等互相垂直,每一条对角线平分一组对角回顾上节课知识点:ABCDO判定方法1菱形定义互相垂直,每一条对角线平分一组对角ABCDO判定方法1有一组邻边相等的 平行四边形是菱形
逆命题原命题菱形的四条边相等四条边相等的四边形是菱形or四条边相等的平行四边形是菱形怎么证明逆命题的准确性呢?判定方法2已知:如图,四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.证明:∵AB=BC=CD=AD;
∴AB=CD , BC=AD.
∴四边形ABCD是平行四边形.
又∵AB=BC,
∴四边形ABCD是菱形.
四条边相等的四边形是菱形符号语言:因为 AB=BC=CD=AD
所以 四边形ABCD是菱形判定方法2ABCDO逆命题原命题菱形的对角线互相垂直对角线互相垂直的平行四边形是菱形判定方法3对角线互相垂直的四边形是不是菱形?逆命题原命题菱形的对角线互相垂直对角线互相垂直的平行四边形是菱形判定方法3举反例:证明: ∵四边形ABC是平行四边形
∴OA=OC
又∵ AC ⊥ BD;
∴BA=BC
∴ ABCD是菱形
对角线互相垂直的平行四边形是菱形符号语言:因为 四边形ABCD是
平行四边形
AC⊥BD
所以 平行四边形ABCD是菱形判定方法3ABCDO第三节 课堂练习又∵四边形ABCD是平行四边形,∵ OA=4,OB=3,AB=5,证明:即AC⊥BD,∴ AB2=OA2+OB2,∴△AOB是直角三角形,∴四边形ABCD是菱形. 1. 判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直且平分的四边形是菱形;
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形;
(4) 有一条对角线平分一组对角的
平行四边形是菱形.√ ╳ ╳ √ 2. □ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是 形; (2)若AC=BD,则□ABCD是 形; (3)若∠ABC是直角,则□ABCD是 形; (4)若∠BAO=∠DAO,则□ABCD是 形。
菱菱矩矩3.下列命题中正确的是( )
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形4.下列条件中,
不能判定四边形ABCD为菱形的是( )
A.AC⊥BD,AC与BD互相平分
B.AB=BC=CD=DA
C.AB=BC,AD=CD,且AC⊥BD
D.AB=CD,AD=BC,AC⊥BD
CC3. 如图,顺次连接矩形ABCD各边的中点,得到四边形EFGH.求证:四边形EFGH是菱形.证明:因为 四边形ABCD是矩形
所以 ∠A=∠B,AD=BC
又因为 E,FG,H是各边的中点
所以 AE=BG,AF=BF
所以 △AEF≌△BGF(SAS)
所以 EF=GF
同理可得 EH=GH,EF,EH,GH=GF
所以 EF=GF=GH=EH
所以 四边形EFGH是菱形
第四节 课堂小结课堂小结一组邻边相等对角线互相垂直四条边相等五种判定方法菱形的判定方法:感谢观看
