华师大版八年级上册数学13.3.2等腰三角形的判定课件(共18张PPT)
文档属性
| 名称 | 华师大版八年级上册数学13.3.2等腰三角形的判定课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 193.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-05 19:19:39 | ||
图片预览





文档简介
(共18张PPT)
13.3.2等腰三角形的判定
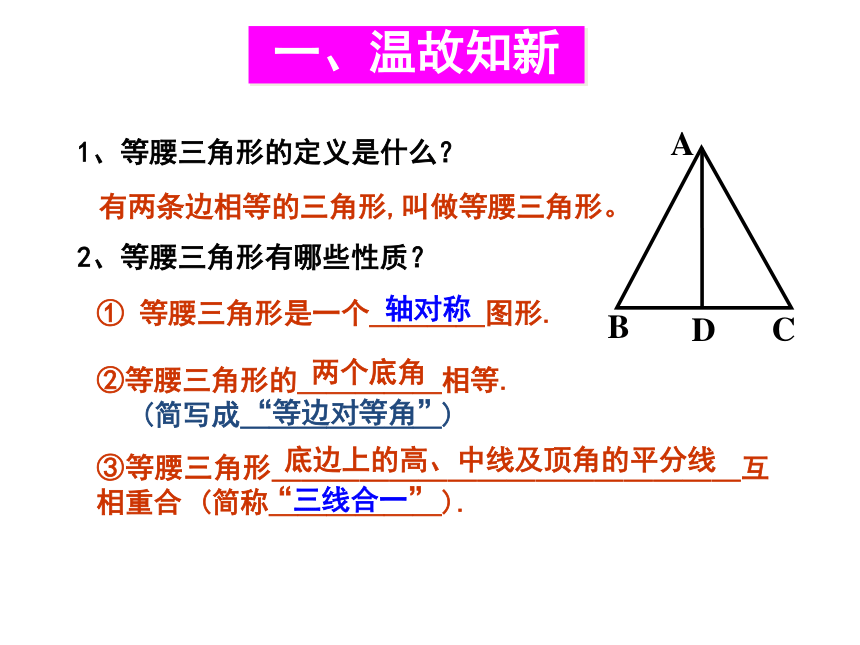
1、等腰三角形的定义是什么?
有两条边相等的三角形,叫做等腰三角形。
D
A
B
C
一、温故知新
③等腰三角形________________互相重合 (简称______).
②等腰三角形的_____相等.
(简写成_______)
2、等腰三角形有哪些性质?
① 等腰三角形是一个____图形.
轴对称
两个底角
“等边对等角”
底边上的高、中线及顶角的平分线
“三线合一”
方法1:定义
有两条边相等的三角形,
叫做等腰三角形。
如何判定一个三角形是等腰三角形?
二、提出问题
要测量金字塔这样大型的建筑物是否为等腰三角形,你的方法是什么?
等腰三角形
两底角相等
?
两角相等
等腰三角形
三、新知探索
画图验证 动手做一做
1.在卡纸上画一条线段BC。
2.分别以点B和点C为顶点,以BC为始边,用量角器画两
个相等的角,两角终边的交点为A,得到△ ABC,并把它剪下来。
3.用刻度尺找出BC的中点D,连接AD,然后沿AD对折。
问题1:AB与AC是否重合?
问题2:同学们你得出的结论如何用文字语言加以叙述?
探究一 等腰三角形的判定方法
几何画板演示
发现结论:
如果一个三角形有两个角相等,那么这两个角所对的边也相等。
(简写成“等角对等边”)
命题:如果一个三角形有两个角相等,那么这两个角所对的边也相等.(简写成“等角对等边”)
已知:如图,在△ABC中,∠B=∠C
求证:AB=AC。
A
C
B
分析:AB=AC
全等三角形对应边相等
构造两个全等三角形
添加辅助线
推理证明
命题:如果一个三角形有两个角相等,那么这两个角所对的边也相等.(简写成“等角对等边”)
已知:如图,在△ABC中,∠B=∠C
求证:AB=AC。
推理证明
A
⌒
⌒
B
C
添加辅助线方法:
⌒⌒
1
2
方法一:作∠A的角平分线AD
方法二:作BC边上的中线AD
方法三:作BC边上的高AD
D
A
B
C
如果一个三角形有两个角相等,那么这两个角所对的边也相等
几何语言:在△ABC中
∵∠B =∠C (已知)
∴ AB=AC(等角对等边)
等腰三角形的判定定理:
(简写成“等角对等边”)。
归纳
等腰三角形的判定方法有两种:
①定义 ②判定定理
测量两角相等可以判定金字塔形状为等腰三角形。
如图,下列推理正确吗?
∵∠1=∠2
∴ DC=BC
A
B
C
D
2
1
(等角对等边)
错,因为∠1和∠2 不是同一个三角形的内角。
(已知)
四、学以致用
注意:在同一个三角形中应用哟!
例1:如图,在△ABC中,已知∠A= 40° ,∠B= 70°。
求证:AB=AC
A
B
C
40°
70°
∴ ∠C= 180° — ∠A — ∠B
= 180° —40° — 70°= 70°
∴ ∠C =∠B(等量代换)
∴AB=AC
证明: ∵∠A+∠B +∠C= 180°
∠A= 40° ,∠B= 70°(已知)
(三角形的内角和等于 )
180°
A
B
C
D
E
1
2
例2.已知: AD平分∠CAE ,AD∥BC。
求证:AB=AC
等腰三角形的判定定理是证明
线段相等的一种重要的方法
变式 已知: BD平分∠ABC , AD∥BC 。
求证: AB=AD
A
B
C
D
1
2
3
证明:
∵ BD平分∠ABC
∴ ∠ 1 = ∠2( )
角平分线的定义
∵ AD∥BC
∴ ∠ 1 = ∠3( )
两直线平行,内错角相等
∴ ∠ 2= ∠ 3( )
等量代换
∴ AB=AD( )
等角对等边
(1)一个角的角平分线
(2)平行于角的一边的直线
等腰三角形
等腰三角形的判定
等腰三角形的判定方法
等腰三角形添加辅助线的方法
两边相等的三角形
两角相等
的三角形
“三线合一”
等腰三角形的判定定理是证明
线段相等的一种重要的方法
五、课堂小结
必做题:课本第84页 第5 ,6 ,7题
2. 选作题:自主探究等边三角形的判定方法。
六、布置作业
13.3.2等腰三角形的判定
1、等腰三角形的定义是什么?
有两条边相等的三角形,叫做等腰三角形。
D
A
B
C
一、温故知新
③等腰三角形________________互相重合 (简称______).
②等腰三角形的_____相等.
(简写成_______)
2、等腰三角形有哪些性质?
① 等腰三角形是一个____图形.
轴对称
两个底角
“等边对等角”
底边上的高、中线及顶角的平分线
“三线合一”
方法1:定义
有两条边相等的三角形,
叫做等腰三角形。
如何判定一个三角形是等腰三角形?
二、提出问题
要测量金字塔这样大型的建筑物是否为等腰三角形,你的方法是什么?
等腰三角形
两底角相等
?
两角相等
等腰三角形
三、新知探索
画图验证 动手做一做
1.在卡纸上画一条线段BC。
2.分别以点B和点C为顶点,以BC为始边,用量角器画两
个相等的角,两角终边的交点为A,得到△ ABC,并把它剪下来。
3.用刻度尺找出BC的中点D,连接AD,然后沿AD对折。
问题1:AB与AC是否重合?
问题2:同学们你得出的结论如何用文字语言加以叙述?
探究一 等腰三角形的判定方法
几何画板演示
发现结论:
如果一个三角形有两个角相等,那么这两个角所对的边也相等。
(简写成“等角对等边”)
命题:如果一个三角形有两个角相等,那么这两个角所对的边也相等.(简写成“等角对等边”)
已知:如图,在△ABC中,∠B=∠C
求证:AB=AC。
A
C
B
分析:AB=AC
全等三角形对应边相等
构造两个全等三角形
添加辅助线
推理证明
命题:如果一个三角形有两个角相等,那么这两个角所对的边也相等.(简写成“等角对等边”)
已知:如图,在△ABC中,∠B=∠C
求证:AB=AC。
推理证明
A
⌒
⌒
B
C
添加辅助线方法:
⌒⌒
1
2
方法一:作∠A的角平分线AD
方法二:作BC边上的中线AD
方法三:作BC边上的高AD
D
A
B
C
如果一个三角形有两个角相等,那么这两个角所对的边也相等
几何语言:在△ABC中
∵∠B =∠C (已知)
∴ AB=AC(等角对等边)
等腰三角形的判定定理:
(简写成“等角对等边”)。
归纳
等腰三角形的判定方法有两种:
①定义 ②判定定理
测量两角相等可以判定金字塔形状为等腰三角形。
如图,下列推理正确吗?
∵∠1=∠2
∴ DC=BC
A
B
C
D
2
1
(等角对等边)
错,因为∠1和∠2 不是同一个三角形的内角。
(已知)
四、学以致用
注意:在同一个三角形中应用哟!
例1:如图,在△ABC中,已知∠A= 40° ,∠B= 70°。
求证:AB=AC
A
B
C
40°
70°
∴ ∠C= 180° — ∠A — ∠B
= 180° —40° — 70°= 70°
∴ ∠C =∠B(等量代换)
∴AB=AC
证明: ∵∠A+∠B +∠C= 180°
∠A= 40° ,∠B= 70°(已知)
(三角形的内角和等于 )
180°
A
B
C
D
E
1
2
例2.已知: AD平分∠CAE ,AD∥BC。
求证:AB=AC
等腰三角形的判定定理是证明
线段相等的一种重要的方法
变式 已知: BD平分∠ABC , AD∥BC 。
求证: AB=AD
A
B
C
D
1
2
3
证明:
∵ BD平分∠ABC
∴ ∠ 1 = ∠2( )
角平分线的定义
∵ AD∥BC
∴ ∠ 1 = ∠3( )
两直线平行,内错角相等
∴ ∠ 2= ∠ 3( )
等量代换
∴ AB=AD( )
等角对等边
(1)一个角的角平分线
(2)平行于角的一边的直线
等腰三角形
等腰三角形的判定
等腰三角形的判定方法
等腰三角形添加辅助线的方法
两边相等的三角形
两角相等
的三角形
“三线合一”
等腰三角形的判定定理是证明
线段相等的一种重要的方法
五、课堂小结
必做题:课本第84页 第5 ,6 ,7题
2. 选作题:自主探究等边三角形的判定方法。
六、布置作业
