北师大版七年级数学下空中课堂4.1认识三角形1课件(27张ppt)
文档属性
| 名称 | 北师大版七年级数学下空中课堂4.1认识三角形1课件(27张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-05 19:34:08 | ||
图片预览







文档简介
课件27张PPT。第四章 三角形第1节 认识三角形1北师大版七年级(下册)数学观察图片欣赏图片:首欣赏图片:欣赏图片:1、理解三角形的概念,认识它的 边、角及顶点等各部分.2、理解三角形的分类.3、掌握三角形的内角和定理.三角形相关概念:
(先自学再以小组为单位交流预习情况,最后进行小组展示.)
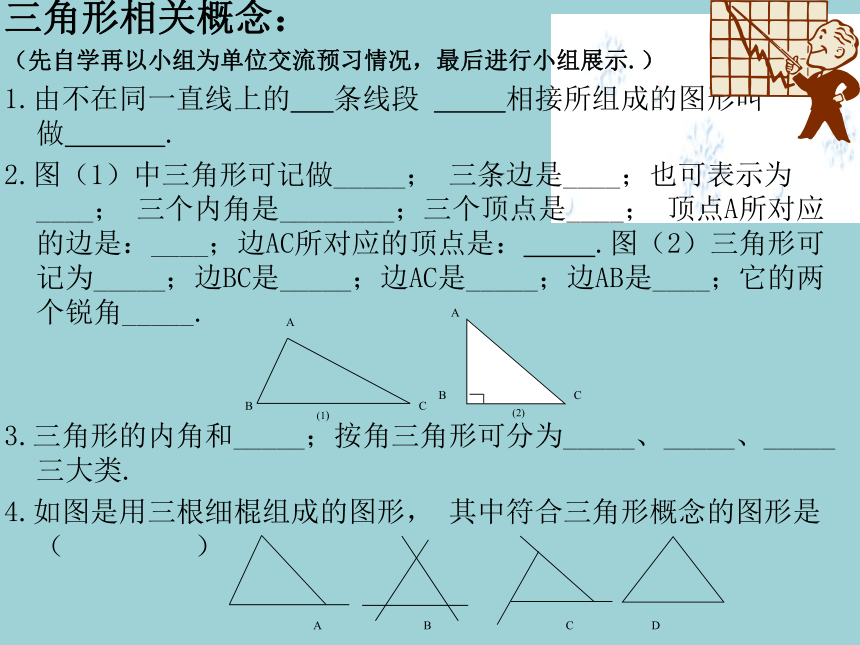
1.由不在同一直线上的 条线段 相接所组成的图形叫做 .
2.图(1)中三角形可记做_____; 三条边是____;也可表示为____; 三个内角是________;三个顶点是____; 顶点A所对应的边是:____;边AC所对应的顶点是: .图(2)三角形可记为_____;边BC是_____;边AC是_____;边AB是____;它的两个锐角_____.
3.三角形的内角和_____;按角三角形可分为_____、_____、_____三大类.
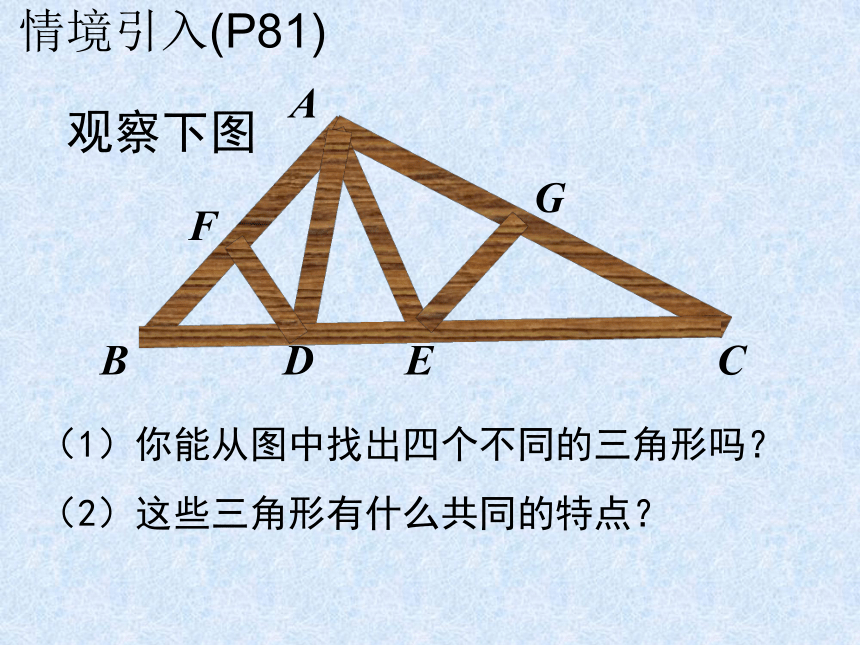
4.如图是用三根细棍组成的图形, 其中符合三角形概念的图形是( )(1)你能从图中找出四个不同的三角形吗?
(2)这些三角形有什么共同的特点?观察下图ABCDEFG情境引入(P81)ABCDEFG 由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。1、什么叫做三角形?自主探究(P81)2、如何表示三角形? 三角形可用符号“△”表示,如右图三角形记作:ACB自主探究 (P81)△ABCacb3、三角形的边怎么表示? 如图三角形中三边可表示为AB,BC,AC,顶点A所对的边BC也可表示为a,顶点B所对的边AC表示为b,顶点C所对的边AB表示c 。ACB展示提升(P81)acb边:三角形中有三条边:AB,BC,AC角:三角形中有三个角:∠A,∠B,∠C顶点:三角形中有三个顶点:顶点A,顶点B,顶点C问题1ACBacb 如果说三角形有“三要素”,
你能猜出是哪三要素吗?(1)做一个三角形纸片,它的三个内角分别为∠1,∠2和∠3,如下图。(2)将∠1撕下,并按上图进行摆放,其中∠1的顶点与∠2的顶点重合,它的一条边与∠2的一条边重合。此时∠1的另一条边 b与∠3的一条边 a 平行吗?为什么?a b (3)将∠3与∠2的公共边延长,它与 b 所夹的角为∠4。∠3与∠4的大小有什么关系?为什么?问题2(P81)ED证法一方法一已知:△A B C.
求证:∠A +∠B +∠C=180°证明:在△A B C的外部以C A 为边作∠A C E =∠A. 延长B C至D 。
∵ ∠A C E =∠A
∴AB∥CE
∴ ∠B =∠ECD
∵ ∠BCA+∠ACE+∠ECD=180°
∴ ∠A+∠B+∠BCA= 180°ACBDE12过点C作CE//AB
延长BC3证明:方法二(1)下图中小明所拿三角形被遮住的两个内角是什么角?小颖的
呢?试着说明理由.(2)下图中三角形被遮住的两个内角可能是什么角?将所
得结果与(1)的结果进行比较.三角形的分类锐角三角形三个内角都是锐角钝角三角形有一个内角是钝角直角三角形有一个内角是直角按三角形内角的大小把三角形分为三类问题3(P83)直角边直角边斜边1、常用符号“Rt?ABC”来表示直角三角形ABC。2、思考:直角三角形的两个锐角之间有什么关系?直角三角形的两个锐角
互余直角三角形问题4(P83)观察下面的三角形,并把它们的标号,填入相应圈内:锐角三角形 直角三角形 钝角三角形③⑤①④⑥②⑦抢答(P83)76543211、已知∠A,∠B,∠C是△ABC的三个内角,∠A = 70°,∠C = 30°,∠B =( )。
2、直角三角形一个锐角为70°,另一个锐角( )。
3、在△ABC中,∠A=80°,∠B=∠C,则∠C=( )。
4、如果△ABC中,∠A:∠B:∠C=2:3:5,此三角形按角分类应为( )。80°20°50°直角三角形小试牛刀有关三角形的角度计算问题,有两种类型:
一是直接利用三角形的内角和180°进行计算;
二是设某一个角为x(或将某一个角视为未知数),其余的角用x的代数式表示,从而根据题意列出方程(组)求解。归纳总结 一个三角形中会有两个直角吗?
可能两个内角是钝角或锐角吗?探索拓广……请谈谈您的收获1.观察下面的三角形,并把它们的标号填入相应图内:
2.如下图(1)所示,图中共有 个三角形,其中以AB为一边的三角形有 个,以∠C为一个内角的三角形有 个.
3.如下图(2),以∠C为内角的三角形有 和 .在这两个三角形中,∠C的对边分别为 和 .
4.已知:∠A、∠B、∠C是△ABC的三个内角,∠A=70°,∠C=30 °,
∠B= .
5.如果△ABC中,∠A∶∠B∶∠C=2∶3∶5,此三角形按角分类应为 .
6.如图(3)△ABC中,点D,E分别在边AC,BC上,已知DE∥AB, ∠A=40 °,∠1=80 ° ,求∠C的度数.达标检测:课本p84 习题4.1 第2、3、4题。助学从88--91页,4.1认识三角形
(先自学再以小组为单位交流预习情况,最后进行小组展示.)
1.由不在同一直线上的 条线段 相接所组成的图形叫做 .
2.图(1)中三角形可记做_____; 三条边是____;也可表示为____; 三个内角是________;三个顶点是____; 顶点A所对应的边是:____;边AC所对应的顶点是: .图(2)三角形可记为_____;边BC是_____;边AC是_____;边AB是____;它的两个锐角_____.
3.三角形的内角和_____;按角三角形可分为_____、_____、_____三大类.
4.如图是用三根细棍组成的图形, 其中符合三角形概念的图形是( )(1)你能从图中找出四个不同的三角形吗?
(2)这些三角形有什么共同的特点?观察下图ABCDEFG情境引入(P81)ABCDEFG 由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。1、什么叫做三角形?自主探究(P81)2、如何表示三角形? 三角形可用符号“△”表示,如右图三角形记作:ACB自主探究 (P81)△ABCacb3、三角形的边怎么表示? 如图三角形中三边可表示为AB,BC,AC,顶点A所对的边BC也可表示为a,顶点B所对的边AC表示为b,顶点C所对的边AB表示c 。ACB展示提升(P81)acb边:三角形中有三条边:AB,BC,AC角:三角形中有三个角:∠A,∠B,∠C顶点:三角形中有三个顶点:顶点A,顶点B,顶点C问题1ACBacb 如果说三角形有“三要素”,
你能猜出是哪三要素吗?(1)做一个三角形纸片,它的三个内角分别为∠1,∠2和∠3,如下图。(2)将∠1撕下,并按上图进行摆放,其中∠1的顶点与∠2的顶点重合,它的一条边与∠2的一条边重合。此时∠1的另一条边 b与∠3的一条边 a 平行吗?为什么?a b (3)将∠3与∠2的公共边延长,它与 b 所夹的角为∠4。∠3与∠4的大小有什么关系?为什么?问题2(P81)ED证法一方法一已知:△A B C.
求证:∠A +∠B +∠C=180°证明:在△A B C的外部以C A 为边作∠A C E =∠A. 延长B C至D 。
∵ ∠A C E =∠A
∴AB∥CE
∴ ∠B =∠ECD
∵ ∠BCA+∠ACE+∠ECD=180°
∴ ∠A+∠B+∠BCA= 180°ACBDE12过点C作CE//AB
延长BC3证明:方法二(1)下图中小明所拿三角形被遮住的两个内角是什么角?小颖的
呢?试着说明理由.(2)下图中三角形被遮住的两个内角可能是什么角?将所
得结果与(1)的结果进行比较.三角形的分类锐角三角形三个内角都是锐角钝角三角形有一个内角是钝角直角三角形有一个内角是直角按三角形内角的大小把三角形分为三类问题3(P83)直角边直角边斜边1、常用符号“Rt?ABC”来表示直角三角形ABC。2、思考:直角三角形的两个锐角之间有什么关系?直角三角形的两个锐角
互余直角三角形问题4(P83)观察下面的三角形,并把它们的标号,填入相应圈内:锐角三角形 直角三角形 钝角三角形③⑤①④⑥②⑦抢答(P83)76543211、已知∠A,∠B,∠C是△ABC的三个内角,∠A = 70°,∠C = 30°,∠B =( )。
2、直角三角形一个锐角为70°,另一个锐角( )。
3、在△ABC中,∠A=80°,∠B=∠C,则∠C=( )。
4、如果△ABC中,∠A:∠B:∠C=2:3:5,此三角形按角分类应为( )。80°20°50°直角三角形小试牛刀有关三角形的角度计算问题,有两种类型:
一是直接利用三角形的内角和180°进行计算;
二是设某一个角为x(或将某一个角视为未知数),其余的角用x的代数式表示,从而根据题意列出方程(组)求解。归纳总结 一个三角形中会有两个直角吗?
可能两个内角是钝角或锐角吗?探索拓广……请谈谈您的收获1.观察下面的三角形,并把它们的标号填入相应图内:
2.如下图(1)所示,图中共有 个三角形,其中以AB为一边的三角形有 个,以∠C为一个内角的三角形有 个.
3.如下图(2),以∠C为内角的三角形有 和 .在这两个三角形中,∠C的对边分别为 和 .
4.已知:∠A、∠B、∠C是△ABC的三个内角,∠A=70°,∠C=30 °,
∠B= .
5.如果△ABC中,∠A∶∠B∶∠C=2∶3∶5,此三角形按角分类应为 .
6.如图(3)△ABC中,点D,E分别在边AC,BC上,已知DE∥AB, ∠A=40 °,∠1=80 ° ,求∠C的度数.达标检测:课本p84 习题4.1 第2、3、4题。助学从88--91页,4.1认识三角形
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
