湘教版八年级上册数学2.1.3三角形的内角和定理课件(共28张PPT)
文档属性
| 名称 | 湘教版八年级上册数学2.1.3三角形的内角和定理课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-05 20:05:23 | ||
图片预览




文档简介
(共28张PPT)
2.1 三角形
第3课时 三角形的内角和定理
我们已经知道,任意一个三角形的内角和等于180°.怎么验证这个结论呢?
方法一:度量法 通过具体的度量,验证三角形的内角和为180°.
想一想
方法二:拼合法 把三个角拼在一起试试看?
方法三:推理验证法.
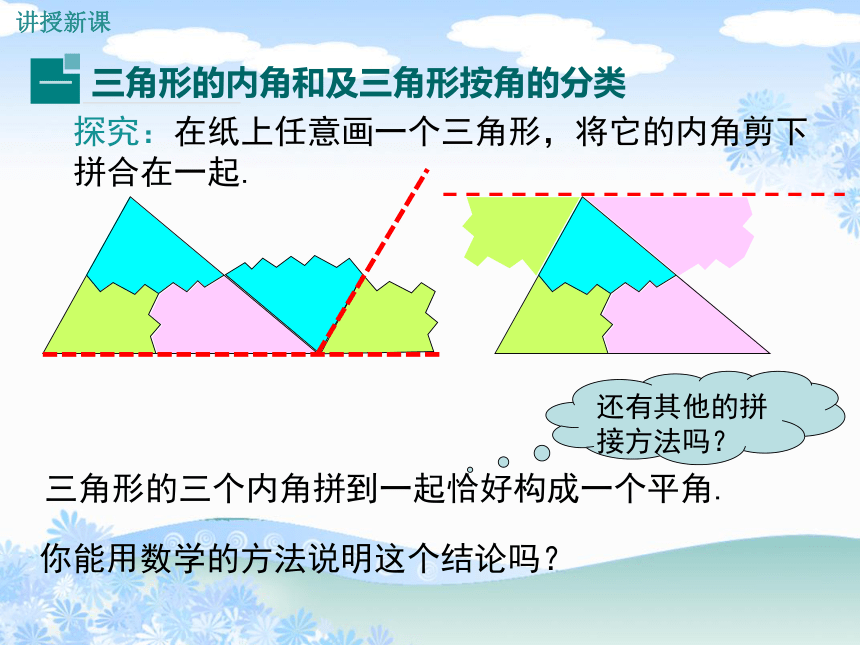
三角形的三个内角拼到一起恰好构成一个平角.
你能用数学的方法说明这个结论吗?
还有其他的拼接方法吗?
讲授新课
探究:在纸上任意画一个三角形,将它的内角剪下拼合在一起.
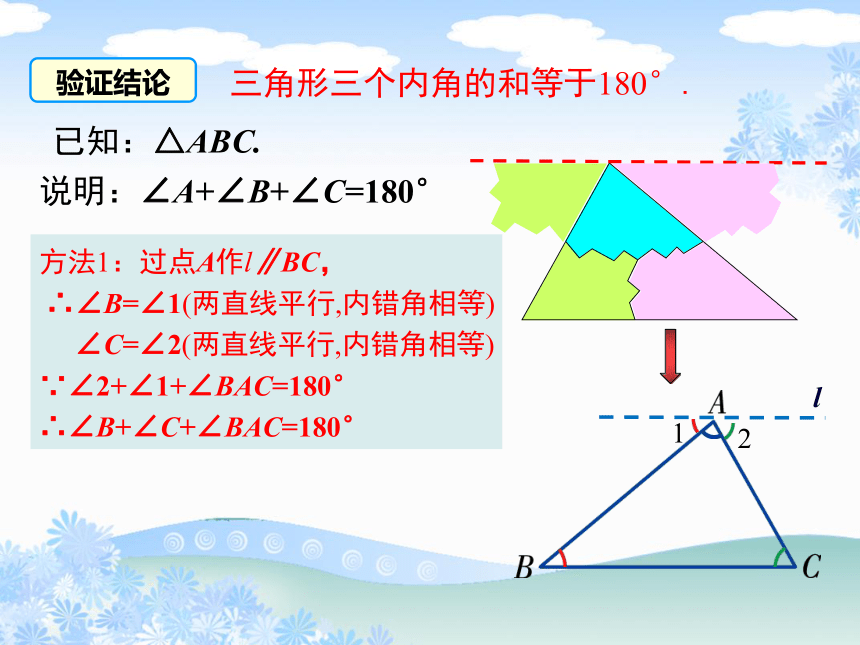
验证结论
三角形三个内角的和等于180°.
说明:∠A+∠B+∠C=180°
已知:△ABC.
方法1:过点A作l∥BC,
∴∠B=∠1(两直线平行,内错角相等)
∠C=∠2(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°
∴∠B+∠C+∠BAC=180°
1
2
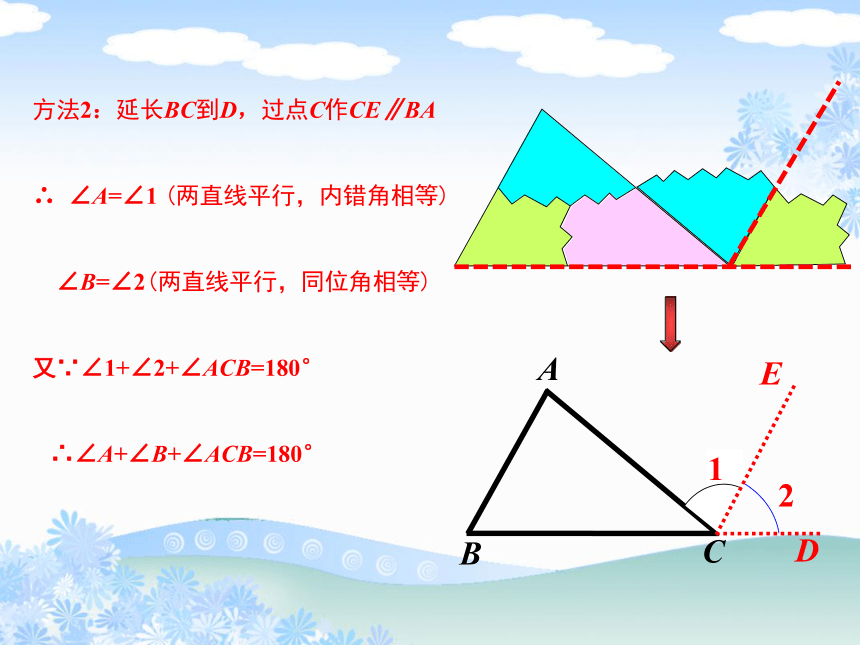
方法2:延长BC到D,过点C作CE∥BA
∴ ∠A=∠1 (两直线平行,内错角相等)
∠B=∠2(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
E
D
E
D
F
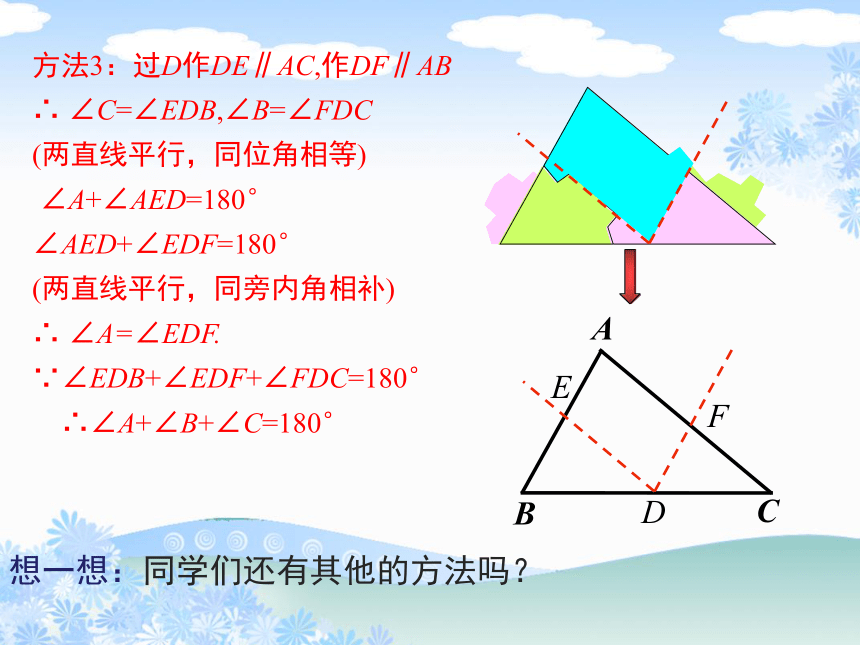
方法3:过D作DE∥AC,作DF∥AB
∴ ∠C=∠EDB,∠B=∠FDC
(两直线平行,同位角相等)
∠A+∠AED=180°
∠AED+∠EDF=180°
(两直线平行,同旁内角相补)
∴ ∠A=∠EDF.
∵∠EDB+∠EDF+∠FDC=180°
∴∠A+∠B+∠C=180°
想一想:同学们还有其他的方法吗?
三角形内角和定理: 三角形内角和等于180°.
(3)在△ABC中, ∠A=40 ° ,∠A=2∠B,则∠C=___.
102 °
40 °
120°
(1)在△ABC中,∠A=35°,∠ B=43 ° , 则 ∠ C=
(2)在△ABC中,∠C=90°,∠B=50 ° ,则∠A=___.
x+2x+ 90=180,
x=30.
x+x+x=180,
x=60.
图(1)
图(2)
(4)求出图中x的值.
例1 如图,在△ABC中, ∠BAC=40°,∠B=75°,AD是△ABC的角平分线,求∠ADB的度数.
解:∵AD是△ABC的角平分线∠BAC=40 °
在△ABD中
∠ADB=180°-∠B-∠BAD
=180°-75°-20°
=85°.
典例精析
【变式题】如图,CD是∠ACB的平分线,DE∥BC,∠A=50°,∠B=70°,求∠EDC,∠BDC的度数.
解:∵∠A=50°,∠B=70°
∴∠ACB=180°-∠A-∠B=60°
∵CD是∠ACB的平分线
∴∠BCD= ∠ACB=30°
∵DE∥BC
∴∠EDC=∠BCD=30°
在△BDC中,∠BDC=180°-∠B-∠BCD=80°
例2 如图,△ABC中,D在BC的延长线上,过D作DE⊥AB于E,交AC于F.已知∠A=30°,∠FCD=80°,求∠D.
解:∵DE⊥AB,∴∠FEA=90°
∵在△AEF中,∠FEA=90°,∠A=30°
∴∠AFE=180°-∠FEA-∠A=60
又∵∠CFD=∠AFE
∴∠CFD=60°
在△CDF中,∠CFD=60°,∠FCD=80°
∴ ∠D=180°-∠CFD-∠FCD=40°
基本图形
由三角形的内角和易得∠A+∠B=∠C+∠D.
由三角形的内角和易得∠1+∠2=∠3+∠4.
总结归纳
例3 在△ABC 中, ∠A 的度数是∠B 的度数的3倍,∠C 比∠B 大15°,求∠A,∠B,∠C的度数.
解: 设∠B为x°,则∠A为(3x)°
∠C为(x + 15)°, 根据题意得
3x + x +(x + 15)= 180
解得 x = 33
所以 3x = 99 , x + 15 = 48
即 ∠A, ∠B, ∠C的度数分别为99°, 33°, 48°
和差倍分问题借助方程来解. 这是一个重要的数学思想.
(1)一个三角形中最多有 个直角?为什么?
(2)一个三角形中最多有 个钝角?为什么?
(3)一个三角形中至少有 个锐角?为什么?
(4)任意 一个三角形中,最大的一个角的度数至少为 .
60°
2
1
1
三角形中,三个角都是锐角的三角形叫 ,
有一个角是直角的三角形叫 ,
有一个角是钝角的三角形叫 如图所示.
锐角三角形
直角三角形
钝角三角形
直角三角形可用符号“Rt△”来表示,例如直角三角形ABC可以记作“Rt△ABC”.在直角三角形中,夹直角的两边叫作直角边,直角的对边叫作斜边.两条直角边相等的直角三角形叫作等腰直角三角形.
如图,把△ABC的一边BC延长,得到∠ACD.像这样,三角形的一边与另一边的延长线所组成的角,叫作三角形的外角.
对外角∠ACD来说,∠ACB是与它相邻的内角,∠A,∠B是与它不相邻的内角.
F
A
B
C
D
E
如图,∠ BEC是哪个三角形的外角?∠AEC是哪个三角形的外角?∠EFD是哪个三角形的外角?
∠BEC是△AEC的外角;
∠AEC是△BEC的外角;
∠EFD是△BEF和△DCF的外角.
练一练
问题1 如图,△ABC的外角∠BCD与其相邻的内角
∠ACB有什么关系?
∠BCD与∠ACB互补.
问题2 如图,△ABC的外角∠BCD与其不相邻的两内角(∠A,∠B)有什么关系?
∵∠A+∠B+∠ACB=180°
∠BCD+∠ACB=180°
∴∠A+∠B=∠BCD
你能用作平行线的方法证明此结论吗?
D
解:过C作CE平行于AB,
A
B
C
∴∠1= ∠B,(两直线平行,同位角相等)
∠2= ∠A ,(两直线平行,内错角相等)
∴∠ACD= ∠1+ ∠2= ∠A+ ∠B.
已知:如图,△ABC,试说明:∠ACD=∠A+∠B.
验证结论
三角形外角的性质:
三角形的外角等于与它不相邻的两个内角的和.
应用格式:
∵ ∠ACD是△ABC的一个外角
∴ ∠ACD= ∠A+ ∠B.
知识要点
练一练:说出下列图形中∠1和∠2的度数:
∠1=40 °, ∠2=140 °
∠1=18 °, ∠2=130 °
1
2
F
G
解:∵∠1是△FBE的外角,
∴∠1=∠B+ ∠E,
同理∠2=∠A+∠D.
在△CFG中,
∠C+∠1+∠2=180?,
∴∠A+ ∠ B+∠C+ ∠ D+∠E
= 180?.
5.如图,求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数.
能力提升:
考考自己?
在△ABC中,∠A=80°,∠B=∠C , 求∠C的度数.
解:在△ABC中,
∠A+∠B+∠C=180°,∠A=80°.
∴∠B+∠C=100°.
∵∠B=∠C,
∴∠B=∠C=50°.
考考自己?
已知三角形三个内角的度数之比为1:3:5,求这三个内角的度数.
解:设三个内角度数分别为:x、3x、5x.
由题意得: x+3x+5x=180°,
x=20°.
答:三个内角度数分别为20°,60°,100°.
2.1 三角形
第3课时 三角形的内角和定理
我们已经知道,任意一个三角形的内角和等于180°.怎么验证这个结论呢?
方法一:度量法 通过具体的度量,验证三角形的内角和为180°.
想一想
方法二:拼合法 把三个角拼在一起试试看?
方法三:推理验证法.
三角形的三个内角拼到一起恰好构成一个平角.
你能用数学的方法说明这个结论吗?
还有其他的拼接方法吗?
讲授新课
探究:在纸上任意画一个三角形,将它的内角剪下拼合在一起.
验证结论
三角形三个内角的和等于180°.
说明:∠A+∠B+∠C=180°
已知:△ABC.
方法1:过点A作l∥BC,
∴∠B=∠1(两直线平行,内错角相等)
∠C=∠2(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°
∴∠B+∠C+∠BAC=180°
1
2
方法2:延长BC到D,过点C作CE∥BA
∴ ∠A=∠1 (两直线平行,内错角相等)
∠B=∠2(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
E
D
E
D
F
方法3:过D作DE∥AC,作DF∥AB
∴ ∠C=∠EDB,∠B=∠FDC
(两直线平行,同位角相等)
∠A+∠AED=180°
∠AED+∠EDF=180°
(两直线平行,同旁内角相补)
∴ ∠A=∠EDF.
∵∠EDB+∠EDF+∠FDC=180°
∴∠A+∠B+∠C=180°
想一想:同学们还有其他的方法吗?
三角形内角和定理: 三角形内角和等于180°.
(3)在△ABC中, ∠A=40 ° ,∠A=2∠B,则∠C=___.
102 °
40 °
120°
(1)在△ABC中,∠A=35°,∠ B=43 ° , 则 ∠ C=
(2)在△ABC中,∠C=90°,∠B=50 ° ,则∠A=___.
x+2x+ 90=180,
x=30.
x+x+x=180,
x=60.
图(1)
图(2)
(4)求出图中x的值.
例1 如图,在△ABC中, ∠BAC=40°,∠B=75°,AD是△ABC的角平分线,求∠ADB的度数.
解:∵AD是△ABC的角平分线∠BAC=40 °
在△ABD中
∠ADB=180°-∠B-∠BAD
=180°-75°-20°
=85°.
典例精析
【变式题】如图,CD是∠ACB的平分线,DE∥BC,∠A=50°,∠B=70°,求∠EDC,∠BDC的度数.
解:∵∠A=50°,∠B=70°
∴∠ACB=180°-∠A-∠B=60°
∵CD是∠ACB的平分线
∴∠BCD= ∠ACB=30°
∵DE∥BC
∴∠EDC=∠BCD=30°
在△BDC中,∠BDC=180°-∠B-∠BCD=80°
例2 如图,△ABC中,D在BC的延长线上,过D作DE⊥AB于E,交AC于F.已知∠A=30°,∠FCD=80°,求∠D.
解:∵DE⊥AB,∴∠FEA=90°
∵在△AEF中,∠FEA=90°,∠A=30°
∴∠AFE=180°-∠FEA-∠A=60
又∵∠CFD=∠AFE
∴∠CFD=60°
在△CDF中,∠CFD=60°,∠FCD=80°
∴ ∠D=180°-∠CFD-∠FCD=40°
基本图形
由三角形的内角和易得∠A+∠B=∠C+∠D.
由三角形的内角和易得∠1+∠2=∠3+∠4.
总结归纳
例3 在△ABC 中, ∠A 的度数是∠B 的度数的3倍,∠C 比∠B 大15°,求∠A,∠B,∠C的度数.
解: 设∠B为x°,则∠A为(3x)°
∠C为(x + 15)°, 根据题意得
3x + x +(x + 15)= 180
解得 x = 33
所以 3x = 99 , x + 15 = 48
即 ∠A, ∠B, ∠C的度数分别为99°, 33°, 48°
和差倍分问题借助方程来解. 这是一个重要的数学思想.
(1)一个三角形中最多有 个直角?为什么?
(2)一个三角形中最多有 个钝角?为什么?
(3)一个三角形中至少有 个锐角?为什么?
(4)任意 一个三角形中,最大的一个角的度数至少为 .
60°
2
1
1
三角形中,三个角都是锐角的三角形叫 ,
有一个角是直角的三角形叫 ,
有一个角是钝角的三角形叫 如图所示.
锐角三角形
直角三角形
钝角三角形
直角三角形可用符号“Rt△”来表示,例如直角三角形ABC可以记作“Rt△ABC”.在直角三角形中,夹直角的两边叫作直角边,直角的对边叫作斜边.两条直角边相等的直角三角形叫作等腰直角三角形.
如图,把△ABC的一边BC延长,得到∠ACD.像这样,三角形的一边与另一边的延长线所组成的角,叫作三角形的外角.
对外角∠ACD来说,∠ACB是与它相邻的内角,∠A,∠B是与它不相邻的内角.
F
A
B
C
D
E
如图,∠ BEC是哪个三角形的外角?∠AEC是哪个三角形的外角?∠EFD是哪个三角形的外角?
∠BEC是△AEC的外角;
∠AEC是△BEC的外角;
∠EFD是△BEF和△DCF的外角.
练一练
问题1 如图,△ABC的外角∠BCD与其相邻的内角
∠ACB有什么关系?
∠BCD与∠ACB互补.
问题2 如图,△ABC的外角∠BCD与其不相邻的两内角(∠A,∠B)有什么关系?
∵∠A+∠B+∠ACB=180°
∠BCD+∠ACB=180°
∴∠A+∠B=∠BCD
你能用作平行线的方法证明此结论吗?
D
解:过C作CE平行于AB,
A
B
C
∴∠1= ∠B,(两直线平行,同位角相等)
∠2= ∠A ,(两直线平行,内错角相等)
∴∠ACD= ∠1+ ∠2= ∠A+ ∠B.
已知:如图,△ABC,试说明:∠ACD=∠A+∠B.
验证结论
三角形外角的性质:
三角形的外角等于与它不相邻的两个内角的和.
应用格式:
∵ ∠ACD是△ABC的一个外角
∴ ∠ACD= ∠A+ ∠B.
知识要点
练一练:说出下列图形中∠1和∠2的度数:
∠1=40 °, ∠2=140 °
∠1=18 °, ∠2=130 °
1
2
F
G
解:∵∠1是△FBE的外角,
∴∠1=∠B+ ∠E,
同理∠2=∠A+∠D.
在△CFG中,
∠C+∠1+∠2=180?,
∴∠A+ ∠ B+∠C+ ∠ D+∠E
= 180?.
5.如图,求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数.
能力提升:
考考自己?
在△ABC中,∠A=80°,∠B=∠C , 求∠C的度数.
解:在△ABC中,
∠A+∠B+∠C=180°,∠A=80°.
∴∠B+∠C=100°.
∵∠B=∠C,
∴∠B=∠C=50°.
考考自己?
已知三角形三个内角的度数之比为1:3:5,求这三个内角的度数.
解:设三个内角度数分别为:x、3x、5x.
由题意得: x+3x+5x=180°,
x=20°.
答:三个内角度数分别为20°,60°,100°.
同课章节目录
