北师大版七年级数学下册 1.1 同底数幂的乘法 课件(共31张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 1.1 同底数幂的乘法 课件(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-04 00:00:00 | ||
图片预览










文档简介
(共31张PPT)
第一章 整式的乘除
1.1 同底数幂的乘法
同底数幂的乘法法则
同底数幂的乘法法则的应用
逐点
导讲练
课堂小结
作业提升
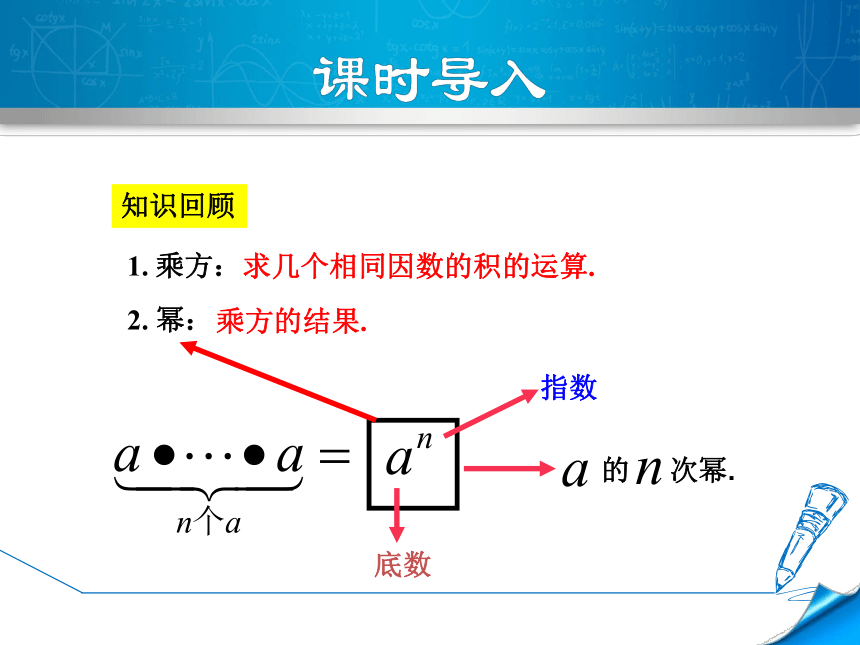
指数
的 次幂.
求几个相同因数的积的运算.
1. 乘方:
2. 幂:
乘方的结果.
知识回顾
1
知识点
同底数幂的乘法法则
知1-导
光在真空中的速度大约是3×108 m/s. 太阳系以外距离
地球最近的恒星是 比邻星,它发出的光到达地球大约
需要4.22年.
一年以3×107s计算,比邻星与地球的距离约为多少?
3×108×3×107×4.22
=37.98×(108×107).
108×107等于多少呢?
知1-导
知1-导
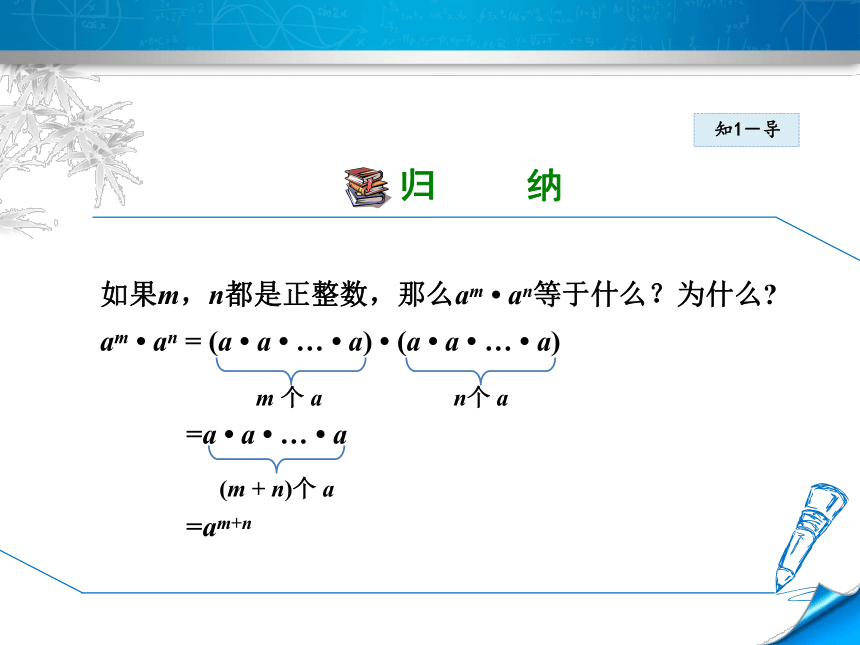
如果m,n都是正整数,那么am ? an等于什么?为什么?
am ? an = (a ? a ? … ? a) ? (a ? a ? … ? a)
=a ? a ? … ? a
=am+n
m 个 a
n个 a
(m + n)个 a
am · an =
同底数幂相乘,
底数 ,指数 .
不变
相加
同底数幂的乘法公式:
am+n (m、n都是正整数)
知1-讲
运算形式(同底、乘法),
运算方法(底不变、指相加)
当三个或三个以上同底数幂相乘时,是否也具有这一
性质呢? 怎样用公式表示?
am·an·ap =
(m,n,p都是正整数)
am·an·ap
=(am· an ) · ap
=am+n· ap
=am+n+p
am+n+p
=(a·a· … ·a)(a·a· … ·a)(a·a· … ·a)
am·an·ap
n个a
m个a
p个a
=am+n+p
或
知1-讲
知1-讲
例1 计算:
(1) (-3)7×(-3)6;(2)
(3) -x3 ? x5; (4) b2m ? b2m+1
解:(1) (-3)7×(-3)6 = (-3)7+6 = (-3)13;
(2)
(3) -x3 ? x5= -x3+5 = -x8 ;
(4) b2m ? b2m+1 = b2m+2m+1 = b4m+1.
(来自《教材》)
知1-讲
例2 计算:(1)(x-y)2 ? (x-y) ? (x-y)5;
(2)(a+b)2 ? (a+b)5;
(3)(x+3)3 ? (x+3)5 ? (x+3).
导引:分别将x-y,a+b,x+3看作一个整体,然后
再利用同底数幂的乘法法则进行计算.
解:(1)(x-y)2·(x-y)·(x-y)5=(x-y)2+1+5=(x-y)8;
(2)(a+b)2·(a+b)5=(a+b)2+5=(a+b)7;
(3)(x+3)3·(x+3)5·(x+3)=(x+3)3+5+1=(x+3)9.
底数为多项式的同底数幂相乘时,把底数看作一
个整体,按照同底数幂的乘法法则进行计算,只把指
数相加,底数仍为原多项式;注意:(x+3)9≠x9+39.
知1-讲
1
知1-练
计算:
(1)52×57; (2)7×73×72;
(3) -x2 ?x3; (4)(-c)3 ?(-c)m .
(来自《教材》)
(1)52×57=52+7=59.
(2)7×73×72=71+3+2=76.
(3)-x2·x3=-x2+3=-x5.
(4)(-c)3·(-c)m=(-c)3+m.
解:
知1-练
2
下列各式中是同底数幂的是( )
A.23与32
B.a3与(-a)3
C.(m-n)5与(m-n)6
D.(a-b)2与(b-a)3
C
知1-练
3
【中考·连云港】计算a·a2的结果是( )
A.a B.a2
C.2a2 D.a3
D
5
计算(-y2)·y3的结果是( )
A.y5 B.-y5 C.y6 D.-y6
B
若a·a3·am=a8,则m=________.
8
4
知1-练
9
用幂的形式表示结果:(x-y)2·(y-x)3=_______________________.
【中考·安徽】按一定规律排列的一列数:21,22,23,25,28,213,…,若x,y,z表示这列数中的连续三个数,猜想x,y,z满足的关系式是________.
-(x-y)5(或(y-x)5)
10
xy=z
知2-导
2
知识点
同底数幂的乘法法则的应用
同底数幂的乘法法则既可以正用,也
可以逆用. 当其逆用时am+n =am ? an .
知2-讲
(1)同底数幂的乘法法则对于三个同底数幂相乘
同样适用.
即:am·an·ap=am+n+p(m,n,p都是正整数).
(2)同底数幂的乘法法则可逆用,即am+n=am·an(m,n
都是正整数).
(3)底数可以是一个单项式,也可以是一个多项式;在
幂的运算中常用到下面两种变形:
①(-a)n=
an(n为偶数)
-an(n为奇数)
(b-a)n(n为偶数)
-(b-a)n(n为奇数)
②(a-b)n=
知2-讲
例3 光在真空中的速度约为3×108 m/s,太阳光照射到地球上大约需要 5×102s.地球距离太阳大约有多远?
解:3×108×5×102
=15×1010
= 1.5×1011(m).
地球距离太阳大约有1.5×1011m.
(来自《教材》)
用科学记数法表示两个数相乘时,常把10n看作底数
相同的幂参与运算,而把其他部分看作常数参与运算,
然后把两者再相乘或直接表示为科学记数法的形式.
知2-讲
例4 已知am=2,an=5,求am+n的值.
导引:分将同底数幂的乘法法则逆用,可求出am+n
的值.
解:am+n=am·an=2×5=10.
知2-讲
当幂的指数是和的形式时,可逆向运用同底数幂的乘
法法则,将幂指数和转化为同底数幂相乘,然后把幂
作为一个整体代入变形后的幂的运算式中求解.
知2-讲
知2-练
1
一种电子计算机每秒可做4×109次运算,它工作
5 ×102s可做多少次运算?
(来自《教材》)
4×109×5×102=4×5×109×102
=20×1011
=2×1012(次),
所以它工作5×102 s可做2×1012次运算.
解:
知2-练
(来自《教材》)
2
解决本节课一开始比邻星到地球的距离问题.
3×108×3×107×4.22=37.98×1015
=3.798×1016 (m),
所以比邻星与地球的距离约为3.798×1016 m.
解:
知2-练
3
【中考·大庆】若am=2,an=8,则am+n=________.
计算(a+b)3·(a+b)2m·(a+b)n的结果为( )
A.(a+b)6m+n B.(a+b)2m+n+3
C.(a+b)2mn+3 D.(a+b)6mn
4
16
B
知2-练
5
x3m+3可以写成( )
A.3xm+1 B.x3m+x3
C.x3·xm+1 D.x3m·x3
计算(-2)2 019+(-2)2 018的结果是( )
A.-22 018 B.22 018
C.-22 019 D.22 019
6
D
A
知2-练
8
一个长方形的长是4.2×104cm,宽是2×104cm,求此长方形的面积及周长.
面积=长×宽=4.2×104×2×104
=8.4×108(cm2).
周长=2(长+宽)=2×(4.2×104+2×104)
=1.24×105(cm).
综上可得长方形的面积为8.4×108cm2,
周长为1.24×105cm.
解:
知2-练
9
已知2x=5,2y=7,2z=35.试说明:x+y=z.
因为2x=5,2y=7,2z=35,
所以2x·2y=5×7=35=2z.
又因为2x·2y=2x+y,所以2x+y=2z.
所以x+y=z.
解:
1. 同底数幂的乘法法则:
同底数幂相乘,底数不变,指数相加.
即: am ? an = am+n (m,n 都是正整数)
2. 同底数幂的乘法法则可逆用.
即am+n=am·an(m,n 都是正整数).
1
知识小结
请分析以下解答过程是否正确,如不正确,请写出
正确的解答过程.
易错点:对法则理解不透导致错误
2
易错小结
(1)(2)(3)的解答过程均不正确,正确的解答过程如下:
(1)x?x3=x1+3=x4.
(2)(-x)2?(-x)4=(-x)2+4=(-x)6=x6.
(3)x4?x3=x4+3=x7.
解:
(1)x的指数是1时省略不写,误以为指数是0;(2)幂的符号错误;(3)同底数幂相乘,底数不变,指数相加,误以为指数相乘.
第一章 整式的乘除
1.1 同底数幂的乘法
同底数幂的乘法法则
同底数幂的乘法法则的应用
逐点
导讲练
课堂小结
作业提升
指数
的 次幂.
求几个相同因数的积的运算.
1. 乘方:
2. 幂:
乘方的结果.
知识回顾
1
知识点
同底数幂的乘法法则
知1-导
光在真空中的速度大约是3×108 m/s. 太阳系以外距离
地球最近的恒星是 比邻星,它发出的光到达地球大约
需要4.22年.
一年以3×107s计算,比邻星与地球的距离约为多少?
3×108×3×107×4.22
=37.98×(108×107).
108×107等于多少呢?
知1-导
知1-导
如果m,n都是正整数,那么am ? an等于什么?为什么?
am ? an = (a ? a ? … ? a) ? (a ? a ? … ? a)
=a ? a ? … ? a
=am+n
m 个 a
n个 a
(m + n)个 a
am · an =
同底数幂相乘,
底数 ,指数 .
不变
相加
同底数幂的乘法公式:
am+n (m、n都是正整数)
知1-讲
运算形式(同底、乘法),
运算方法(底不变、指相加)
当三个或三个以上同底数幂相乘时,是否也具有这一
性质呢? 怎样用公式表示?
am·an·ap =
(m,n,p都是正整数)
am·an·ap
=(am· an ) · ap
=am+n· ap
=am+n+p
am+n+p
=(a·a· … ·a)(a·a· … ·a)(a·a· … ·a)
am·an·ap
n个a
m个a
p个a
=am+n+p
或
知1-讲
知1-讲
例1 计算:
(1) (-3)7×(-3)6;(2)
(3) -x3 ? x5; (4) b2m ? b2m+1
解:(1) (-3)7×(-3)6 = (-3)7+6 = (-3)13;
(2)
(3) -x3 ? x5= -x3+5 = -x8 ;
(4) b2m ? b2m+1 = b2m+2m+1 = b4m+1.
(来自《教材》)
知1-讲
例2 计算:(1)(x-y)2 ? (x-y) ? (x-y)5;
(2)(a+b)2 ? (a+b)5;
(3)(x+3)3 ? (x+3)5 ? (x+3).
导引:分别将x-y,a+b,x+3看作一个整体,然后
再利用同底数幂的乘法法则进行计算.
解:(1)(x-y)2·(x-y)·(x-y)5=(x-y)2+1+5=(x-y)8;
(2)(a+b)2·(a+b)5=(a+b)2+5=(a+b)7;
(3)(x+3)3·(x+3)5·(x+3)=(x+3)3+5+1=(x+3)9.
底数为多项式的同底数幂相乘时,把底数看作一
个整体,按照同底数幂的乘法法则进行计算,只把指
数相加,底数仍为原多项式;注意:(x+3)9≠x9+39.
知1-讲
1
知1-练
计算:
(1)52×57; (2)7×73×72;
(3) -x2 ?x3; (4)(-c)3 ?(-c)m .
(来自《教材》)
(1)52×57=52+7=59.
(2)7×73×72=71+3+2=76.
(3)-x2·x3=-x2+3=-x5.
(4)(-c)3·(-c)m=(-c)3+m.
解:
知1-练
2
下列各式中是同底数幂的是( )
A.23与32
B.a3与(-a)3
C.(m-n)5与(m-n)6
D.(a-b)2与(b-a)3
C
知1-练
3
【中考·连云港】计算a·a2的结果是( )
A.a B.a2
C.2a2 D.a3
D
5
计算(-y2)·y3的结果是( )
A.y5 B.-y5 C.y6 D.-y6
B
若a·a3·am=a8,则m=________.
8
4
知1-练
9
用幂的形式表示结果:(x-y)2·(y-x)3=_______________________.
【中考·安徽】按一定规律排列的一列数:21,22,23,25,28,213,…,若x,y,z表示这列数中的连续三个数,猜想x,y,z满足的关系式是________.
-(x-y)5(或(y-x)5)
10
xy=z
知2-导
2
知识点
同底数幂的乘法法则的应用
同底数幂的乘法法则既可以正用,也
可以逆用. 当其逆用时am+n =am ? an .
知2-讲
(1)同底数幂的乘法法则对于三个同底数幂相乘
同样适用.
即:am·an·ap=am+n+p(m,n,p都是正整数).
(2)同底数幂的乘法法则可逆用,即am+n=am·an(m,n
都是正整数).
(3)底数可以是一个单项式,也可以是一个多项式;在
幂的运算中常用到下面两种变形:
①(-a)n=
an(n为偶数)
-an(n为奇数)
(b-a)n(n为偶数)
-(b-a)n(n为奇数)
②(a-b)n=
知2-讲
例3 光在真空中的速度约为3×108 m/s,太阳光照射到地球上大约需要 5×102s.地球距离太阳大约有多远?
解:3×108×5×102
=15×1010
= 1.5×1011(m).
地球距离太阳大约有1.5×1011m.
(来自《教材》)
用科学记数法表示两个数相乘时,常把10n看作底数
相同的幂参与运算,而把其他部分看作常数参与运算,
然后把两者再相乘或直接表示为科学记数法的形式.
知2-讲
例4 已知am=2,an=5,求am+n的值.
导引:分将同底数幂的乘法法则逆用,可求出am+n
的值.
解:am+n=am·an=2×5=10.
知2-讲
当幂的指数是和的形式时,可逆向运用同底数幂的乘
法法则,将幂指数和转化为同底数幂相乘,然后把幂
作为一个整体代入变形后的幂的运算式中求解.
知2-讲
知2-练
1
一种电子计算机每秒可做4×109次运算,它工作
5 ×102s可做多少次运算?
(来自《教材》)
4×109×5×102=4×5×109×102
=20×1011
=2×1012(次),
所以它工作5×102 s可做2×1012次运算.
解:
知2-练
(来自《教材》)
2
解决本节课一开始比邻星到地球的距离问题.
3×108×3×107×4.22=37.98×1015
=3.798×1016 (m),
所以比邻星与地球的距离约为3.798×1016 m.
解:
知2-练
3
【中考·大庆】若am=2,an=8,则am+n=________.
计算(a+b)3·(a+b)2m·(a+b)n的结果为( )
A.(a+b)6m+n B.(a+b)2m+n+3
C.(a+b)2mn+3 D.(a+b)6mn
4
16
B
知2-练
5
x3m+3可以写成( )
A.3xm+1 B.x3m+x3
C.x3·xm+1 D.x3m·x3
计算(-2)2 019+(-2)2 018的结果是( )
A.-22 018 B.22 018
C.-22 019 D.22 019
6
D
A
知2-练
8
一个长方形的长是4.2×104cm,宽是2×104cm,求此长方形的面积及周长.
面积=长×宽=4.2×104×2×104
=8.4×108(cm2).
周长=2(长+宽)=2×(4.2×104+2×104)
=1.24×105(cm).
综上可得长方形的面积为8.4×108cm2,
周长为1.24×105cm.
解:
知2-练
9
已知2x=5,2y=7,2z=35.试说明:x+y=z.
因为2x=5,2y=7,2z=35,
所以2x·2y=5×7=35=2z.
又因为2x·2y=2x+y,所以2x+y=2z.
所以x+y=z.
解:
1. 同底数幂的乘法法则:
同底数幂相乘,底数不变,指数相加.
即: am ? an = am+n (m,n 都是正整数)
2. 同底数幂的乘法法则可逆用.
即am+n=am·an(m,n 都是正整数).
1
知识小结
请分析以下解答过程是否正确,如不正确,请写出
正确的解答过程.
易错点:对法则理解不透导致错误
2
易错小结
(1)(2)(3)的解答过程均不正确,正确的解答过程如下:
(1)x?x3=x1+3=x4.
(2)(-x)2?(-x)4=(-x)2+4=(-x)6=x6.
(3)x4?x3=x4+3=x7.
解:
(1)x的指数是1时省略不写,误以为指数是0;(2)幂的符号错误;(3)同底数幂相乘,底数不变,指数相加,误以为指数相乘.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
