高中数学苏教版选修2-3第一章1.4计数应用题课件(共17张PPT)
文档属性
| 名称 | 高中数学苏教版选修2-3第一章1.4计数应用题课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-06 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
1.4 计数应用题
苏教版高二 选修2-3
例1 高二(1)班有30名男生,20名女生,从50名学生中选3名男生,2名女生分别担任班长、副班长、学习委员、文娱委员、体育委员,共有多少种不同的选法?
解:完成这件事情可分三步进行:
第一步:从30名男生中选3名男生,有种方法;
第二步:从20名女生中选2名女生,有种方法;
第三步:将选出的5名学生进行分工,即全排列,有种方法.
根据分步计数原理,共有
=92568000
种选法.
答:共有92568000种不同的选法.
例1 高二(1)班有30名男生,20名女生,从50名学生中选3名男生,2名女生分别担任班长、副班长、学习委员、文娱委员、体育委员,共有多少种不同的选法?
思考
上题如果分两步:先从30名男生中选3名男生担任3种不同职务,再从20名女生中选2名女生担任2种不同职务,则结果为.这样做对吗?为什么?
第一步:从30名男生中选3名男生担任3种不同职务,有种方法;
第二步:从20名女生中选2名女生担任2种不同职务,有种方法.
根据分步计数原理,共有
=92568000
种选法.
解:这样做是不对的,理由如下:
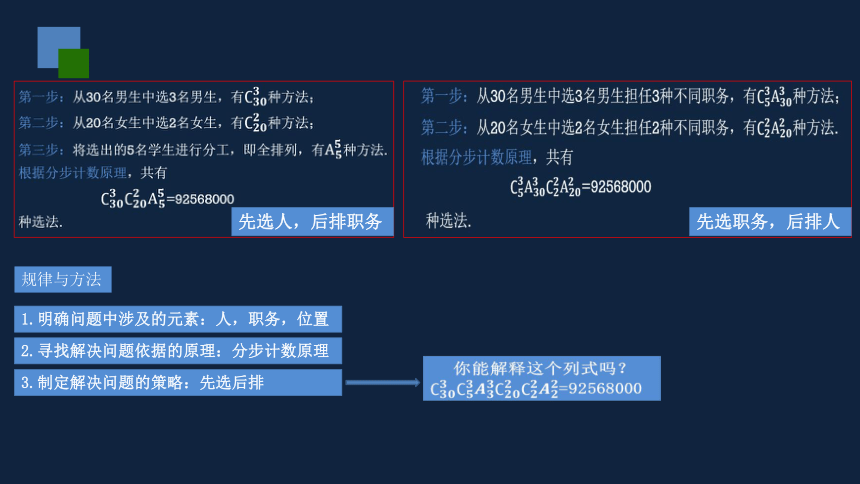
规律与方法
先选人,后排职务
先选职务,后排人
你能解释这个列式吗? =92568000
1.明确问题中涉及的元素:人,职务,位置
3.制定解决问题的策略:先选后排
2.寻找解决问题依据的原理:分步计数原理
例2 2名女生、4名男生排成一排.
(1)2名女生相邻的不同排法共有多少种?
解法一:完成这件事情可分两步进行:
第一步:选出相邻的两个位置排女生,有种排法;
第二步:剩下的四个位置排男生,有种排法.
根据分步计数原理,共有
=240
种排法.
解法二:由于2名女生必须相邻,于是可以将2名女生看成1个元素,与4名男生共5个元素排成一排,不同的排法有种,又因为2名相邻的女生有种排法,因此不同的排法种数共有
=240
捆绑法:
用来解决相邻问题,把相邻的元素看作一个整体
思考
若要求4名男生相邻的不同排法共有多少种?
3=144
先选后排
例2 2名女生、4名男生排成一排.
(2)2名女生不相邻的不同排法共有多少种?
解法一:完成这件事情可分两步进行:
第一步:将4名男生排成一排,有种排法;
第二步:排2名女生.由于2名女生不相邻,于是可以在每2名男生之间及两端共5个位置中选出2个排2名女生,有种排法.
根据分步计数原理,共有=480种排法
解法二:因为2名女生的排法只有相邻与不相邻两种情况,所以由(1)的结果可知,2名女生不相邻的排法种数共有
240=480
插空法:用来解决不相邻问题
思考
若有3名女生,4名男生排成一排,其中3名女生不相邻的不同排法共有多少种?
=1440
(1)2名女生相邻的不同排法共有多少种?(240种)
间接法
例2 2名女生、4名男生排成一排.
(3)女生甲必须排在女生乙的左边(不一定相邻)的不同排法共有多少种?
解法一:完成这件事情可分两步进行:
第一步:排2名女生,由于女生的顺序已经确定,这2名女生的排法种数为从6个位置中选出2个位置的组合数,即为;
第二步:排4名男生,将4名男生在剩下的4个位置上进行排列的方法数有种.
根据分步计数原理,共有=360种排法
解法二:如果将6名学生全排列,共有种不同的排法,其中,在男生位置确定之后,女生的排法数有种,因为女生的顺序已经确定,所以这种排法中,只有一种符合要求,故满足条件的排法种数共有
=360
女甲与女乙两人中“一左一右”的机会是均等的
=360
(2)2名女生不相邻的不同排法共有多少种?(480种)
(1)2名女生相邻的不同排法共有多少种?(240种)
例2 2名女生、4名男生排成一排.
(1)2名女生相邻的不同排法共有多少种?
(2)2名女生不相邻的不同排法共有多少种?
(3)女生甲必须排在女生乙的左边(不一定相邻)的不同排法共有多少种?
1.明确问题中涉及的元素:女生,男生,位置
3.制定解决问题的策略:①一般方法:先选后排(关注特殊元素,特殊位置)
②特殊技巧:捆绑法,插空法,间接法
2.寻找解决问题依据的原理:分步计数原理
规律与方法
例3 从0,1,2,…,9这10个数字中选出5个不同的数字组成五位数,其中大于13000的有多少个?
解法一:满足条件的五位数有两类:
2~9
第一类:万位数大于1,这样的五位数共有个;
1
3~9
第二类:万位数为1,千位数不小于3,这样的五位数共有个;
根据分类计数原理,大于13000的五位数共有
8=26544(个)
例3 从0,1,2,…,9这10个数字中选出5个不同的数字组成五位数,其中大于13000的有多少个?
解法二:
1~9
由0,1,2,…,9这10个数字中不同的5个数字组成的五位数共有个;
1
0,2
其中不大于13000的五位数的万位数都是1,且千位数小于3,这样的数共有个;
所以满足条件的五位数共有
9=26544(个)
例3 从0,1,2,…,9这10个数字中选出5个不同的数字组成五位数,其中大于13000的有多少个?
思考
在例3中,大于13500的数有多少个?
解法一:满足条件的五位数有3类:
2~9
第一类:万位数大于1,这样的五位数共有个;
1
4~9
第二类:万位数为1,千位数不小于4,这样的五位数共有个;
1
5~9
3
第三类:万位数为1,千位数为3,百位数不小于5,这样的五位数共有个;
根据分类计数原理,满足条件的五位数共有
8=26418(个)
例3 从0,1,2,…,9这10个数字中选出5个不同的数字组成五位数,其中大于13000的有多少个?
思考
在例3中,大于13500的数有多少个?
解法二:由例3知,大于13000的五位数共有26544个;
1
0,2,4
3
小于13500的五位数共有个;
所以满足条件的五位数共有
26544=26418(个)
例3 从0,1,2,…,9这10个数字中选出5个不同的数字组成五位数,其中大于13000的有多少个?
思考
在例3组成的五位数中,偶数有多少个?
解:满足条件的偶数有2类
0
第一类:末尾为0,共有个;
2,4,6,8
第二类:末尾为非零偶数,共有4×个;
去掉0,去掉末尾数
根据分类计数原理,满足条件的偶数共有
=13776(个)
课堂小结
1.分析问题中涉及到的元素,关注具有特殊条件的元素,作为优先考虑的对象;
解决计数应用题的策略
2.明确解决问题所依据的原理:分步计数原理,分类计数原理,有时候需要两者结合使用;
3. 解决问题过程中,明确分步的顺序与分类的标准,将一般方法(先选后排)与特殊技巧(捆绑法、插空法、间接法等)结合使用,分类标准要做到不重不漏.
课后练习
一、选择题
1.用数字1,2,3,4,5组成没有重复数字的五位数,其中奇数的个数为( ).
A. 24
B. 48
C. 60
D. 72
2.在实验员操作的实验中,要先后实施6个程序,其中程序A只能出现在第一步,程序B和C实施时必须相邻,请问实验顺序的编排方法共有( )种.
A. 96
B. 24
C. 36
D. 48
3.某学校为了迎接市春季运动会,从5名男生和4名女生组成的田径运动队中选出4人参加比赛,要求男、女生都有,则男生甲与女生乙至少有1人入选的方法种数为( ).
A. 85
B. 86
C. 91
D. 92
4.7个人站成一排,甲、乙2人必须站在两端,不同的排法有( )种.
A. 120
B. 240
C. 360
D. 180
二、填空题
5.由1,2,3,4,5,6组成没有重复数字且1,3都不与5相邻的六位偶数共有 ______个.
6.在8张奖券中有一、二、三等奖各1张,其余5张无奖,将这8张奖券分配给4个人,每人2张,不同的获奖情况有________种.
三、解答题
7.如图所示,在以AB为直径的半圆周上,有异于A,B的六个点C1,C2,…,C6,直径AB上有异于A,B的四个点D1,D2,D3,D4,则:
(1)以这12个点(包括A,B)中的4个点为顶点,可作出多少个四边形?
(2)以这10个点(不包括A,B)中的3个点为顶点,可作出多少个三角形?
其中含点C1的有多少个?
1、D 2、D 3、B 4、B 5、108 6、60
7、(1)构成四边形,需要四个点,且无三点共线,可以分成三类:
①四个点从C1,C2,…,C6中取出,有个四边形;
②三个点从C1,C2,…,C6中取出,另一个点从D1,D2,D3,D4,A,B中取出,有个四边形;
③二个点从C1,C2,…,C6中取出,另外二个点从D1,D2,D3,D4,A,B中取出,有个四边形.
故满足条件的四边形共有N=++=360(个).
(2)类似于(1)可分三种情况讨论得三角形个数为++=116(个).
其中含点C1的有++=36(个).
作业答案:
1.4 计数应用题
苏教版高二 选修2-3
例1 高二(1)班有30名男生,20名女生,从50名学生中选3名男生,2名女生分别担任班长、副班长、学习委员、文娱委员、体育委员,共有多少种不同的选法?
解:完成这件事情可分三步进行:
第一步:从30名男生中选3名男生,有种方法;
第二步:从20名女生中选2名女生,有种方法;
第三步:将选出的5名学生进行分工,即全排列,有种方法.
根据分步计数原理,共有
=92568000
种选法.
答:共有92568000种不同的选法.
例1 高二(1)班有30名男生,20名女生,从50名学生中选3名男生,2名女生分别担任班长、副班长、学习委员、文娱委员、体育委员,共有多少种不同的选法?
思考
上题如果分两步:先从30名男生中选3名男生担任3种不同职务,再从20名女生中选2名女生担任2种不同职务,则结果为.这样做对吗?为什么?
第一步:从30名男生中选3名男生担任3种不同职务,有种方法;
第二步:从20名女生中选2名女生担任2种不同职务,有种方法.
根据分步计数原理,共有
=92568000
种选法.
解:这样做是不对的,理由如下:
规律与方法
先选人,后排职务
先选职务,后排人
你能解释这个列式吗? =92568000
1.明确问题中涉及的元素:人,职务,位置
3.制定解决问题的策略:先选后排
2.寻找解决问题依据的原理:分步计数原理
例2 2名女生、4名男生排成一排.
(1)2名女生相邻的不同排法共有多少种?
解法一:完成这件事情可分两步进行:
第一步:选出相邻的两个位置排女生,有种排法;
第二步:剩下的四个位置排男生,有种排法.
根据分步计数原理,共有
=240
种排法.
解法二:由于2名女生必须相邻,于是可以将2名女生看成1个元素,与4名男生共5个元素排成一排,不同的排法有种,又因为2名相邻的女生有种排法,因此不同的排法种数共有
=240
捆绑法:
用来解决相邻问题,把相邻的元素看作一个整体
思考
若要求4名男生相邻的不同排法共有多少种?
3=144
先选后排
例2 2名女生、4名男生排成一排.
(2)2名女生不相邻的不同排法共有多少种?
解法一:完成这件事情可分两步进行:
第一步:将4名男生排成一排,有种排法;
第二步:排2名女生.由于2名女生不相邻,于是可以在每2名男生之间及两端共5个位置中选出2个排2名女生,有种排法.
根据分步计数原理,共有=480种排法
解法二:因为2名女生的排法只有相邻与不相邻两种情况,所以由(1)的结果可知,2名女生不相邻的排法种数共有
240=480
插空法:用来解决不相邻问题
思考
若有3名女生,4名男生排成一排,其中3名女生不相邻的不同排法共有多少种?
=1440
(1)2名女生相邻的不同排法共有多少种?(240种)
间接法
例2 2名女生、4名男生排成一排.
(3)女生甲必须排在女生乙的左边(不一定相邻)的不同排法共有多少种?
解法一:完成这件事情可分两步进行:
第一步:排2名女生,由于女生的顺序已经确定,这2名女生的排法种数为从6个位置中选出2个位置的组合数,即为;
第二步:排4名男生,将4名男生在剩下的4个位置上进行排列的方法数有种.
根据分步计数原理,共有=360种排法
解法二:如果将6名学生全排列,共有种不同的排法,其中,在男生位置确定之后,女生的排法数有种,因为女生的顺序已经确定,所以这种排法中,只有一种符合要求,故满足条件的排法种数共有
=360
女甲与女乙两人中“一左一右”的机会是均等的
=360
(2)2名女生不相邻的不同排法共有多少种?(480种)
(1)2名女生相邻的不同排法共有多少种?(240种)
例2 2名女生、4名男生排成一排.
(1)2名女生相邻的不同排法共有多少种?
(2)2名女生不相邻的不同排法共有多少种?
(3)女生甲必须排在女生乙的左边(不一定相邻)的不同排法共有多少种?
1.明确问题中涉及的元素:女生,男生,位置
3.制定解决问题的策略:①一般方法:先选后排(关注特殊元素,特殊位置)
②特殊技巧:捆绑法,插空法,间接法
2.寻找解决问题依据的原理:分步计数原理
规律与方法
例3 从0,1,2,…,9这10个数字中选出5个不同的数字组成五位数,其中大于13000的有多少个?
解法一:满足条件的五位数有两类:
2~9
第一类:万位数大于1,这样的五位数共有个;
1
3~9
第二类:万位数为1,千位数不小于3,这样的五位数共有个;
根据分类计数原理,大于13000的五位数共有
8=26544(个)
例3 从0,1,2,…,9这10个数字中选出5个不同的数字组成五位数,其中大于13000的有多少个?
解法二:
1~9
由0,1,2,…,9这10个数字中不同的5个数字组成的五位数共有个;
1
0,2
其中不大于13000的五位数的万位数都是1,且千位数小于3,这样的数共有个;
所以满足条件的五位数共有
9=26544(个)
例3 从0,1,2,…,9这10个数字中选出5个不同的数字组成五位数,其中大于13000的有多少个?
思考
在例3中,大于13500的数有多少个?
解法一:满足条件的五位数有3类:
2~9
第一类:万位数大于1,这样的五位数共有个;
1
4~9
第二类:万位数为1,千位数不小于4,这样的五位数共有个;
1
5~9
3
第三类:万位数为1,千位数为3,百位数不小于5,这样的五位数共有个;
根据分类计数原理,满足条件的五位数共有
8=26418(个)
例3 从0,1,2,…,9这10个数字中选出5个不同的数字组成五位数,其中大于13000的有多少个?
思考
在例3中,大于13500的数有多少个?
解法二:由例3知,大于13000的五位数共有26544个;
1
0,2,4
3
小于13500的五位数共有个;
所以满足条件的五位数共有
26544=26418(个)
例3 从0,1,2,…,9这10个数字中选出5个不同的数字组成五位数,其中大于13000的有多少个?
思考
在例3组成的五位数中,偶数有多少个?
解:满足条件的偶数有2类
0
第一类:末尾为0,共有个;
2,4,6,8
第二类:末尾为非零偶数,共有4×个;
去掉0,去掉末尾数
根据分类计数原理,满足条件的偶数共有
=13776(个)
课堂小结
1.分析问题中涉及到的元素,关注具有特殊条件的元素,作为优先考虑的对象;
解决计数应用题的策略
2.明确解决问题所依据的原理:分步计数原理,分类计数原理,有时候需要两者结合使用;
3. 解决问题过程中,明确分步的顺序与分类的标准,将一般方法(先选后排)与特殊技巧(捆绑法、插空法、间接法等)结合使用,分类标准要做到不重不漏.
课后练习
一、选择题
1.用数字1,2,3,4,5组成没有重复数字的五位数,其中奇数的个数为( ).
A. 24
B. 48
C. 60
D. 72
2.在实验员操作的实验中,要先后实施6个程序,其中程序A只能出现在第一步,程序B和C实施时必须相邻,请问实验顺序的编排方法共有( )种.
A. 96
B. 24
C. 36
D. 48
3.某学校为了迎接市春季运动会,从5名男生和4名女生组成的田径运动队中选出4人参加比赛,要求男、女生都有,则男生甲与女生乙至少有1人入选的方法种数为( ).
A. 85
B. 86
C. 91
D. 92
4.7个人站成一排,甲、乙2人必须站在两端,不同的排法有( )种.
A. 120
B. 240
C. 360
D. 180
二、填空题
5.由1,2,3,4,5,6组成没有重复数字且1,3都不与5相邻的六位偶数共有 ______个.
6.在8张奖券中有一、二、三等奖各1张,其余5张无奖,将这8张奖券分配给4个人,每人2张,不同的获奖情况有________种.
三、解答题
7.如图所示,在以AB为直径的半圆周上,有异于A,B的六个点C1,C2,…,C6,直径AB上有异于A,B的四个点D1,D2,D3,D4,则:
(1)以这12个点(包括A,B)中的4个点为顶点,可作出多少个四边形?
(2)以这10个点(不包括A,B)中的3个点为顶点,可作出多少个三角形?
其中含点C1的有多少个?
1、D 2、D 3、B 4、B 5、108 6、60
7、(1)构成四边形,需要四个点,且无三点共线,可以分成三类:
①四个点从C1,C2,…,C6中取出,有个四边形;
②三个点从C1,C2,…,C6中取出,另一个点从D1,D2,D3,D4,A,B中取出,有个四边形;
③二个点从C1,C2,…,C6中取出,另外二个点从D1,D2,D3,D4,A,B中取出,有个四边形.
故满足条件的四边形共有N=++=360(个).
(2)类似于(1)可分三种情况讨论得三角形个数为++=116(个).
其中含点C1的有++=36(个).
作业答案:
