人教版七年级数学下册8.2 消元---解二元一次方程组第一课时课件(23张)
文档属性
| 名称 | 人教版七年级数学下册8.2 消元---解二元一次方程组第一课时课件(23张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-05 20:40:02 | ||
图片预览





文档简介
(共23张PPT)
第八章 二元一次方程组
8.2 消元——解二元一次方程组(1)
第1课时 代入消元法
学习目标 :
1、会用代入法解二元一次方程组。
2、初步体会解二元一次方程组的基本思 想——“消元”。
1. 把上面两个方程写成用含x的式子表示y的形式.
(2)
课前热身
2.你能把上面两个方程写成用含y的式子表示x的形式?
(1)
(1)
(2)
3.如何解这样的方程组
x + y = 200
y = x + 10
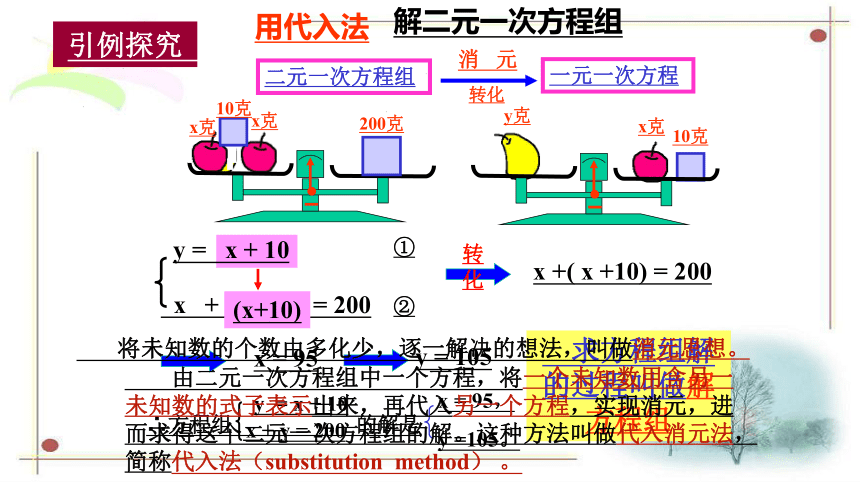
解二元一次方程组
一元一次方程
二元一次方程组
消 元
用代入法
x克
10克
(x+10)
x +( x +10) = 200
①
②
x = 95
y = 105
求方程组解的过程叫做解方程组
转化
将未知数的个数由多化少,逐一解决的想法,叫做消元思想。
由二元一次方程组中一个方程,将一个未知数用含另一未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解。这种方法叫做代入消元法,简称代入法(substitution method) 。
转化
引例探究
解方程组:
y用常数表示
我们发现:
当方程组中有一个未知数已经用含另一个未知数的式子表示时,可以直接代入消元。
下列二元一次方程组如何消元?
y用含x的式子表示
(1)
(2)
解方程组:
下列二元一次方程组如何消元?
y用含x的式子表示
(1)
(2)
y用常数表示
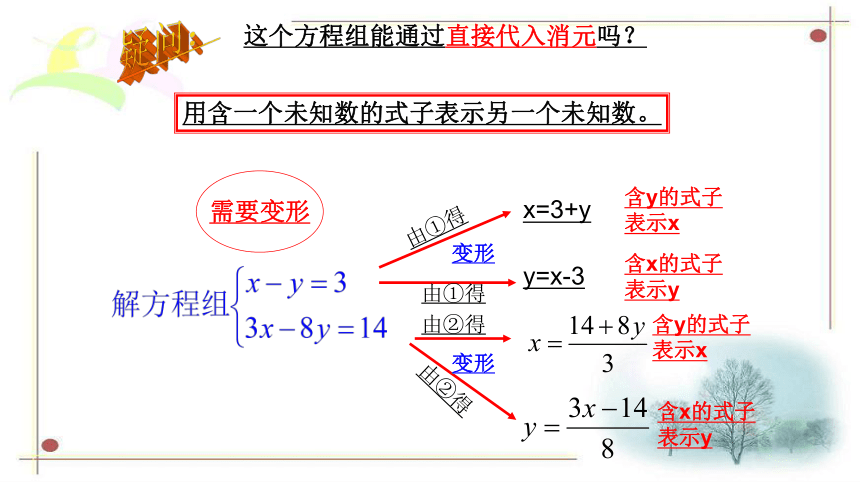
这个方程组能通过直接代入消元吗?
x=3+y
y=x-3
变形
用含一个未知数的式子表示另一个未知数。
由②得
由②得
含y的式子表示x
含x的式子表示y
含y的式子表示x
含x的式子表示y
需要变形
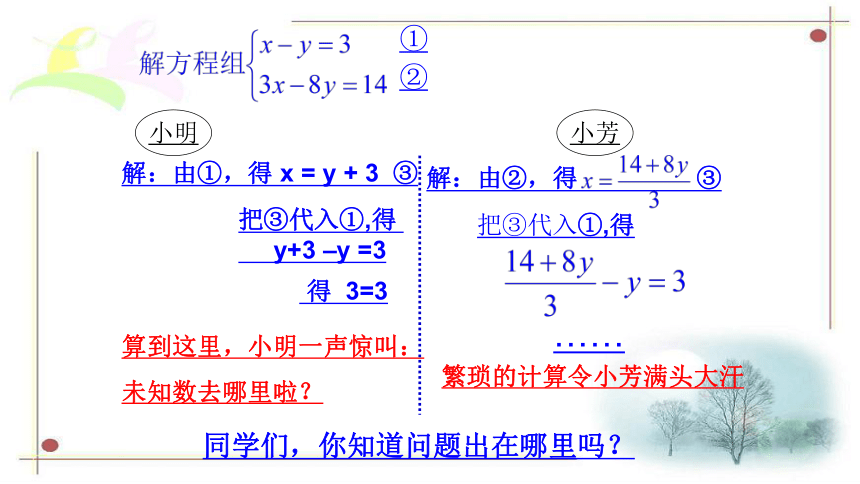
同学们,你知道问题出在哪里吗?
解:由①,得 x = y + 3 ③
把③代入①,得
y+3 –y =3
得 3=3
算到这里,小明一声惊叫:
未知数去哪里啦?
繁琐的计算令小芳满头大汗
解:由②,得 ③
把③代入①,得
……
小明
小芳
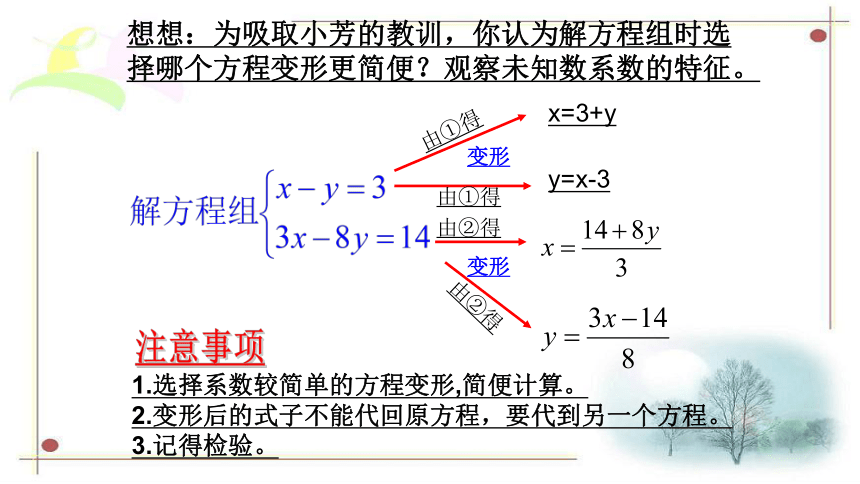
想想:为吸取小芳的教训,你认为解方程组时选择哪个方程变形更简便?观察未知数系数的特征。
1.选择系数较简单的方程变形,简便计算。
2.变形后的式子不能代回原方程,要代到另一个方程。
3.记得检验。
快速问答:1.为简便地解方程组,你会选择哪个方程变形
不用变,把①代入②
变②,由② 得y=3-2x
变①,由① 得y=3x-4
变①,由① 得x=3+y或y=x-3
不用变,把②代入①
一练到位
例2 解方程组
解:
由①得:
x = 3+ y
③
把③代入②得:
3(3+y)– 8y= 14
把y= – 1代入③,得
x = 3+(-1)=2
1、将方程组里的一个方程变形,用含有一个未知数的式子表示另一个未知数;
2、用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
3、把这个未知数的值代入上面的式子,解得另一个未知数的值;
4、写出方程组的解。
变
代
解
写
9+3y– 8y= 14
– 5y= 5
y= – 1
说说方法
二
元
一
次
方
程
组
x-y=3,
3x-8y=14
y=-1
x = 2
解得y
变形
解得x
代入
消x
一元一次方程
3(y+3)-8y=14.
x =y+3.
用y+3代替x,消未知数x.
用代入法解方程组
及时总结,加深记忆
用代入法解方程组 较简单的
方法是( )
A.消y B.消x
C.消x和消y一样 D.无法确定
A
1.快速问答:
练一练
①
②
解:
把②代入①得:
2y – 3(y – 1)= 1
2y – 3y + 3 = 1
2y – 3y = 1 - 3
- y = - 2
y = 2
把y = 2代入②,得
x = y – 1 = 2 – 1 = 1
练一练
代入消元法
再练一练(一练速度,二练正确率):
用代入法解下列方程组:
①
②
解:由①,得y=2x-5… ③
把③代入②,得3x+4(2x-5)= 2
解这个方程,得x=2
把x=2代入③,得y=-1
∴原方程组的解是
2
-1
应用提高
累死我了
想一想:它们各驮多少个包裹?
你还累?这么大的个才比我多驮两个.
哼,我从你背上拿来一个,我的包裹数就是你的2倍!
解:设牛驮x 袋,马驮y袋,根据题意可列方程组:
解这个方程组得:
答:牛驮了7袋包裹,马驮5 袋包裹.
1、若方程5x m-2n+4y 3n-m = 9是关于x、y的二元一次方程,求m 、n 的值.
解:
由题意知,
m - 2n = 1
3n – m = 1
①
②
由①得:
把③代入②得:
m = 1 +2n
③
3n –(1 + 2n)= 1
3n – 1 – 2n = 1
3n-2n = 1+1
n = 2
把n =2 代入③,得:
m = 1 +2n
能力提升
即m 的值是5,n 的值是4.
所以原方程组的解:
2、如果∣y + 3x - 2∣+∣5x + 2y -2∣= 0,求 x 、y 的值.
解:
由题意知,
①
②
由①得:
y = 2 – 3x
把③代入 得:
③
5x + 2(2 – 3x)- 2 = 0
5x + 4 – 6x – 2 = 0
5x – 6x = 2 - 4
-x = -2
x = 2
把x = 2 代入③,得:
y= 2 - 3×2
y= -4
即x 的值是2,y 的值是-4.
能力提升
所以原方程组的解:
②
通过本节课的研究,学习,你有哪些收获?
一种思路:
一般步骤:
一个技巧:
选择系数比较简单的方程进行变形。
一元一次方程
二元一次方程组
转化
消 元
三个一
归纳
数学问题
(二元一次方程组)
实际问题
设未知数
列方程组
解方程组
代入消元法
数学问题的解
(二元一次方程组的解)
实际问题的答案
检验
解决实际问题的基本思路:
1.方程-x+4y=-15用含y的代数式表示x为( )
A.-x=4y-15 B.x=-15+4y
C. x=4y+15 D.x=-4y+15
3.用代入法解方程组 较为简便的方法是( )
A.先把①变形
B.先把②变形
C.可先把①变形,也可先把②变形
D.把①、②同时变形
2.将y=-2x-4代入3x-y=5可得( )
A.3x-(2x+4)=5 B. 3x-(-2x-4)=5
C.3x+2x-4=5 D. 3x-2x+4=5
4.用代入消元法解下列方程组:
①
②
课堂检测
1.方程-x+4y=-15用含y的代数式表示x为( )
A.-x=4y-15 B.x=-15+4y
C. x=4y+15 D.x=-4y+15
C
B
3.用代入法解方程组 较为简便的方法是( )
A.先把①变形
B.先把②变形
C.可先把①变形,也可先把②变形
D.把①、②同时变形
B
2.将y=-2x-4代入3x-y=5可得( )
A.3x-(2x+4)=5 B. 3x-(-2x-4)=5
C.3x+2x-4=5 D. 3x-2x+4=5
4.用代入消元法解下列方程组:
①
②
课堂检测
作业 :智慧学习第一课时
必做题 :学习巩固和学习检测
选做题 :智慧提升
第八章 二元一次方程组
8.2 消元——解二元一次方程组(1)
第1课时 代入消元法
学习目标 :
1、会用代入法解二元一次方程组。
2、初步体会解二元一次方程组的基本思 想——“消元”。
1. 把上面两个方程写成用含x的式子表示y的形式.
(2)
课前热身
2.你能把上面两个方程写成用含y的式子表示x的形式?
(1)
(1)
(2)
3.如何解这样的方程组
x + y = 200
y = x + 10
解二元一次方程组
一元一次方程
二元一次方程组
消 元
用代入法
x克
10克
(x+10)
x +( x +10) = 200
①
②
x = 95
y = 105
求方程组解的过程叫做解方程组
转化
将未知数的个数由多化少,逐一解决的想法,叫做消元思想。
由二元一次方程组中一个方程,将一个未知数用含另一未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解。这种方法叫做代入消元法,简称代入法(substitution method) 。
转化
引例探究
解方程组:
y用常数表示
我们发现:
当方程组中有一个未知数已经用含另一个未知数的式子表示时,可以直接代入消元。
下列二元一次方程组如何消元?
y用含x的式子表示
(1)
(2)
解方程组:
下列二元一次方程组如何消元?
y用含x的式子表示
(1)
(2)
y用常数表示
这个方程组能通过直接代入消元吗?
x=3+y
y=x-3
变形
用含一个未知数的式子表示另一个未知数。
由②得
由②得
含y的式子表示x
含x的式子表示y
含y的式子表示x
含x的式子表示y
需要变形
同学们,你知道问题出在哪里吗?
解:由①,得 x = y + 3 ③
把③代入①,得
y+3 –y =3
得 3=3
算到这里,小明一声惊叫:
未知数去哪里啦?
繁琐的计算令小芳满头大汗
解:由②,得 ③
把③代入①,得
……
小明
小芳
想想:为吸取小芳的教训,你认为解方程组时选择哪个方程变形更简便?观察未知数系数的特征。
1.选择系数较简单的方程变形,简便计算。
2.变形后的式子不能代回原方程,要代到另一个方程。
3.记得检验。
快速问答:1.为简便地解方程组,你会选择哪个方程变形
不用变,把①代入②
变②,由② 得y=3-2x
变①,由① 得y=3x-4
变①,由① 得x=3+y或y=x-3
不用变,把②代入①
一练到位
例2 解方程组
解:
由①得:
x = 3+ y
③
把③代入②得:
3(3+y)– 8y= 14
把y= – 1代入③,得
x = 3+(-1)=2
1、将方程组里的一个方程变形,用含有一个未知数的式子表示另一个未知数;
2、用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
3、把这个未知数的值代入上面的式子,解得另一个未知数的值;
4、写出方程组的解。
变
代
解
写
9+3y– 8y= 14
– 5y= 5
y= – 1
说说方法
二
元
一
次
方
程
组
x-y=3,
3x-8y=14
y=-1
x = 2
解得y
变形
解得x
代入
消x
一元一次方程
3(y+3)-8y=14.
x =y+3.
用y+3代替x,消未知数x.
用代入法解方程组
及时总结,加深记忆
用代入法解方程组 较简单的
方法是( )
A.消y B.消x
C.消x和消y一样 D.无法确定
A
1.快速问答:
练一练
①
②
解:
把②代入①得:
2y – 3(y – 1)= 1
2y – 3y + 3 = 1
2y – 3y = 1 - 3
- y = - 2
y = 2
把y = 2代入②,得
x = y – 1 = 2 – 1 = 1
练一练
代入消元法
再练一练(一练速度,二练正确率):
用代入法解下列方程组:
①
②
解:由①,得y=2x-5… ③
把③代入②,得3x+4(2x-5)= 2
解这个方程,得x=2
把x=2代入③,得y=-1
∴原方程组的解是
2
-1
应用提高
累死我了
想一想:它们各驮多少个包裹?
你还累?这么大的个才比我多驮两个.
哼,我从你背上拿来一个,我的包裹数就是你的2倍!
解:设牛驮x 袋,马驮y袋,根据题意可列方程组:
解这个方程组得:
答:牛驮了7袋包裹,马驮5 袋包裹.
1、若方程5x m-2n+4y 3n-m = 9是关于x、y的二元一次方程,求m 、n 的值.
解:
由题意知,
m - 2n = 1
3n – m = 1
①
②
由①得:
把③代入②得:
m = 1 +2n
③
3n –(1 + 2n)= 1
3n – 1 – 2n = 1
3n-2n = 1+1
n = 2
把n =2 代入③,得:
m = 1 +2n
能力提升
即m 的值是5,n 的值是4.
所以原方程组的解:
2、如果∣y + 3x - 2∣+∣5x + 2y -2∣= 0,求 x 、y 的值.
解:
由题意知,
①
②
由①得:
y = 2 – 3x
把③代入 得:
③
5x + 2(2 – 3x)- 2 = 0
5x + 4 – 6x – 2 = 0
5x – 6x = 2 - 4
-x = -2
x = 2
把x = 2 代入③,得:
y= 2 - 3×2
y= -4
即x 的值是2,y 的值是-4.
能力提升
所以原方程组的解:
②
通过本节课的研究,学习,你有哪些收获?
一种思路:
一般步骤:
一个技巧:
选择系数比较简单的方程进行变形。
一元一次方程
二元一次方程组
转化
消 元
三个一
归纳
数学问题
(二元一次方程组)
实际问题
设未知数
列方程组
解方程组
代入消元法
数学问题的解
(二元一次方程组的解)
实际问题的答案
检验
解决实际问题的基本思路:
1.方程-x+4y=-15用含y的代数式表示x为( )
A.-x=4y-15 B.x=-15+4y
C. x=4y+15 D.x=-4y+15
3.用代入法解方程组 较为简便的方法是( )
A.先把①变形
B.先把②变形
C.可先把①变形,也可先把②变形
D.把①、②同时变形
2.将y=-2x-4代入3x-y=5可得( )
A.3x-(2x+4)=5 B. 3x-(-2x-4)=5
C.3x+2x-4=5 D. 3x-2x+4=5
4.用代入消元法解下列方程组:
①
②
课堂检测
1.方程-x+4y=-15用含y的代数式表示x为( )
A.-x=4y-15 B.x=-15+4y
C. x=4y+15 D.x=-4y+15
C
B
3.用代入法解方程组 较为简便的方法是( )
A.先把①变形
B.先把②变形
C.可先把①变形,也可先把②变形
D.把①、②同时变形
B
2.将y=-2x-4代入3x-y=5可得( )
A.3x-(2x+4)=5 B. 3x-(-2x-4)=5
C.3x+2x-4=5 D. 3x-2x+4=5
4.用代入消元法解下列方程组:
①
②
课堂检测
作业 :智慧学习第一课时
必做题 :学习巩固和学习检测
选做题 :智慧提升
