沪科版九年级下册数学24.7 弧长与扇形面积 课件(共14张PPT)
文档属性
| 名称 | 沪科版九年级下册数学24.7 弧长与扇形面积 课件(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 875.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-05 20:49:26 | ||
图片预览





文档简介
(共14张PPT)
(第一课时)
(1)半径为R的圆,周长是多少?
(2)圆的周长可以看作是多少度的圆心角所对的弧?
C=2πR
360°
(3)n°圆心角所对弧长是多少?
在半径为R 的圆中,n°的圆心角所对的弧长的计算公式为
1.已知弧所对的圆心角为90度,半径是4,则弧长为_________.
2. 已知一条弧的半径为9,弧长为8 ,那么这条弧所对的圆心角为_____。
3. 钟表的轴心到分针针端的长为5cm,那么经过40分钟,分针针端转过的弧长是( )
A. B. C. D.
160°
B
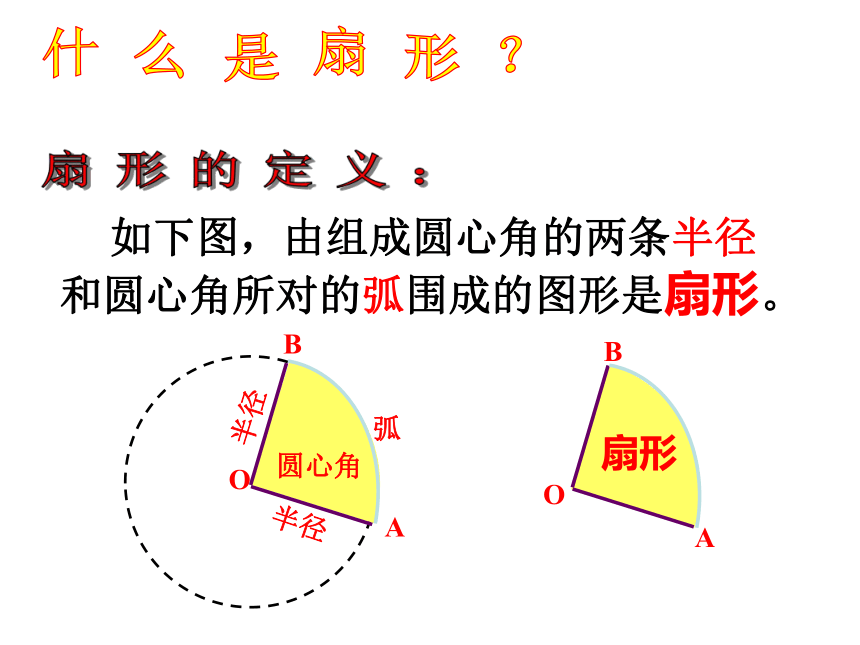
如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
O
圆心角
A
B
探索与思考:
1、半径为R的圆,面积是多少?
2、圆面可以看作是多少度的圆心角所对的扇形?
S=πR2
360°
如果用字母 S 表示扇形的面积,n表示圆心角的度数,R 表示圆半径,那么扇形面积的计算公式是:
那么圆心角为n°的扇形面积是多少?
例:如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积。(精确到0.01cm)。
分析:
弓形的面积
= S扇- S△
解:如图,连接OA、OB,过圆心O作AB的垂线,垂足为D,交弧AB于点C.
∵OC=0.6,DC=0.3 ∴OD=OC-DC=0.3
在Rt△OAD中,OA=0.6,利用勾股定理可得:AD=0.3√3
在Rt△ OAD中,∵OD=1/2OA
∴∠ OAD=30° ∴∠A OD=60°, ∠ AOB=120°
有水部分的面积
1、已知扇形的圆心角为120°,半径为2,则这个扇形的面积,S扇= .
2、已知扇形面积为 ,圆心角为50°,则这个扇形的半径R=____.
6
扇形所对的弧长
扇形的面积是
(1)当已知弧长L和半径R,求扇形面积时,应选用
(2)当已知半径和圆心角的度数,求扇形面积时,应选用
3、已知扇形面积为 ,圆心角为60°,
则这个扇形的半径R=____.
4、已知半径为2cm的扇形,其弧长为 ,
则这个扇形的面积,S扇形=____.
思考:如图,A是半径为1的圆O外一点,且OA=2,AB是⊙O的切线,BC//OA,连结AC,
则阴影部分面积等于 。
(第一课时)
(1)半径为R的圆,周长是多少?
(2)圆的周长可以看作是多少度的圆心角所对的弧?
C=2πR
360°
(3)n°圆心角所对弧长是多少?
在半径为R 的圆中,n°的圆心角所对的弧长的计算公式为
1.已知弧所对的圆心角为90度,半径是4,则弧长为_________.
2. 已知一条弧的半径为9,弧长为8 ,那么这条弧所对的圆心角为_____。
3. 钟表的轴心到分针针端的长为5cm,那么经过40分钟,分针针端转过的弧长是( )
A. B. C. D.
160°
B
如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
O
圆心角
A
B
探索与思考:
1、半径为R的圆,面积是多少?
2、圆面可以看作是多少度的圆心角所对的扇形?
S=πR2
360°
如果用字母 S 表示扇形的面积,n表示圆心角的度数,R 表示圆半径,那么扇形面积的计算公式是:
那么圆心角为n°的扇形面积是多少?
例:如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积。(精确到0.01cm)。
分析:
弓形的面积
= S扇- S△
解:如图,连接OA、OB,过圆心O作AB的垂线,垂足为D,交弧AB于点C.
∵OC=0.6,DC=0.3 ∴OD=OC-DC=0.3
在Rt△OAD中,OA=0.6,利用勾股定理可得:AD=0.3√3
在Rt△ OAD中,∵OD=1/2OA
∴∠ OAD=30° ∴∠A OD=60°, ∠ AOB=120°
有水部分的面积
1、已知扇形的圆心角为120°,半径为2,则这个扇形的面积,S扇= .
2、已知扇形面积为 ,圆心角为50°,则这个扇形的半径R=____.
6
扇形所对的弧长
扇形的面积是
(1)当已知弧长L和半径R,求扇形面积时,应选用
(2)当已知半径和圆心角的度数,求扇形面积时,应选用
3、已知扇形面积为 ,圆心角为60°,
则这个扇形的半径R=____.
4、已知半径为2cm的扇形,其弧长为 ,
则这个扇形的面积,S扇形=____.
思考:如图,A是半径为1的圆O外一点,且OA=2,AB是⊙O的切线,BC//OA,连结AC,
则阴影部分面积等于 。
