高中数学人教B版(2019)必修第三册 第七章7.1.1 角的概念的推广 课件(共20张PPT)
文档属性
| 名称 | 高中数学人教B版(2019)必修第三册 第七章7.1.1 角的概念的推广 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-06 11:12:10 | ||
图片预览





文档简介
(共20张PPT)
概念引入
小游戏:将右手臂向右伸直,记该位置为初始位置。
动作1:逆时针旋转90度;
动作2:顺时针旋转270度;
动作3:逆时针旋转一周半。
生活实例
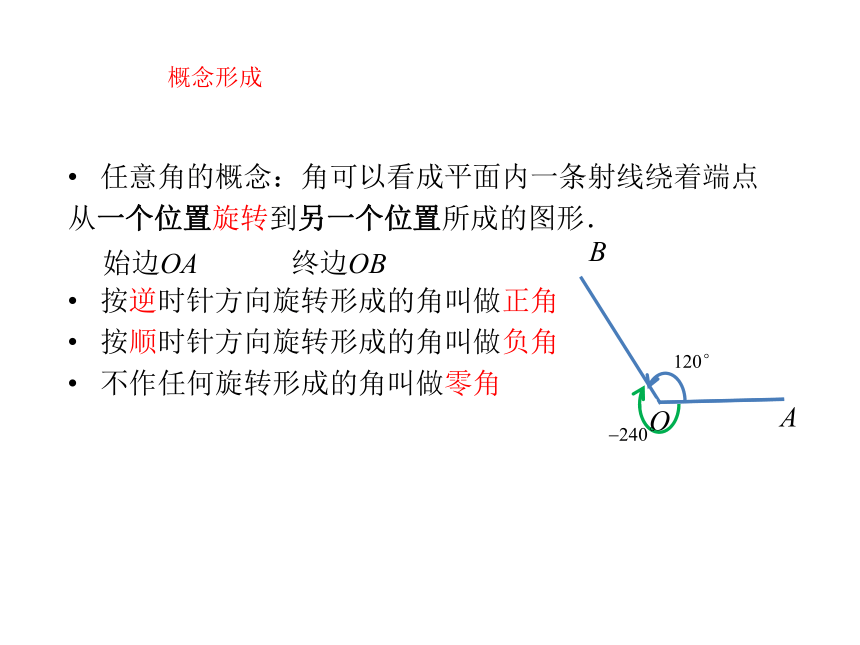
概念形成
任意角的概念:角可以看成平面内一条射线绕着端点
从一个位置旋转到另一个位置所成的图形.
按逆时针方向旋转形成的角叫做正角
按顺时针方向旋转形成的角叫做负角
不作任何旋转形成的角叫做零角
O
A
B
始边OA
终边OB
120°
?240°
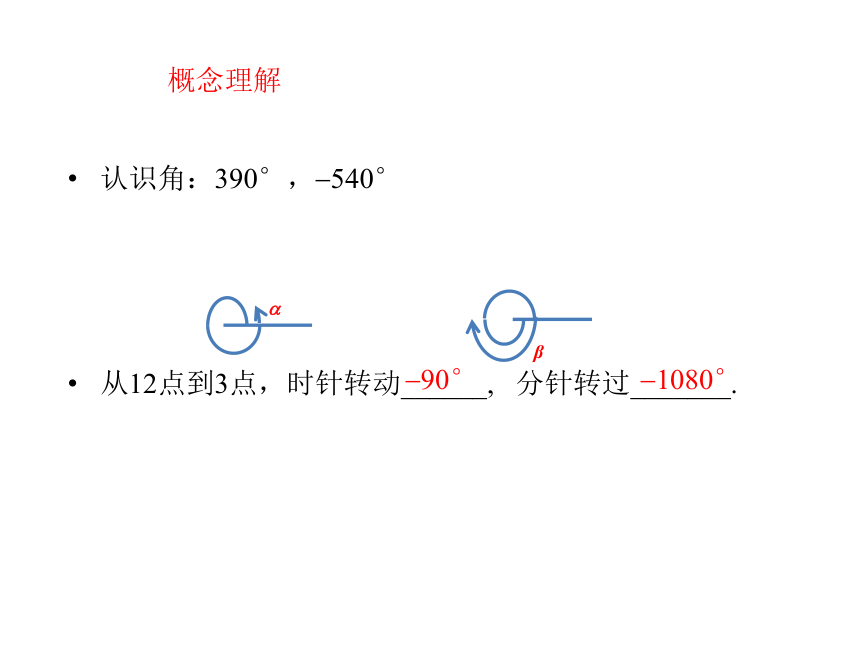
概念理解
认识角:390°,?540°
从12点到3点,时针转动______, 分针转过_______.
?1080°
?90°
?
β
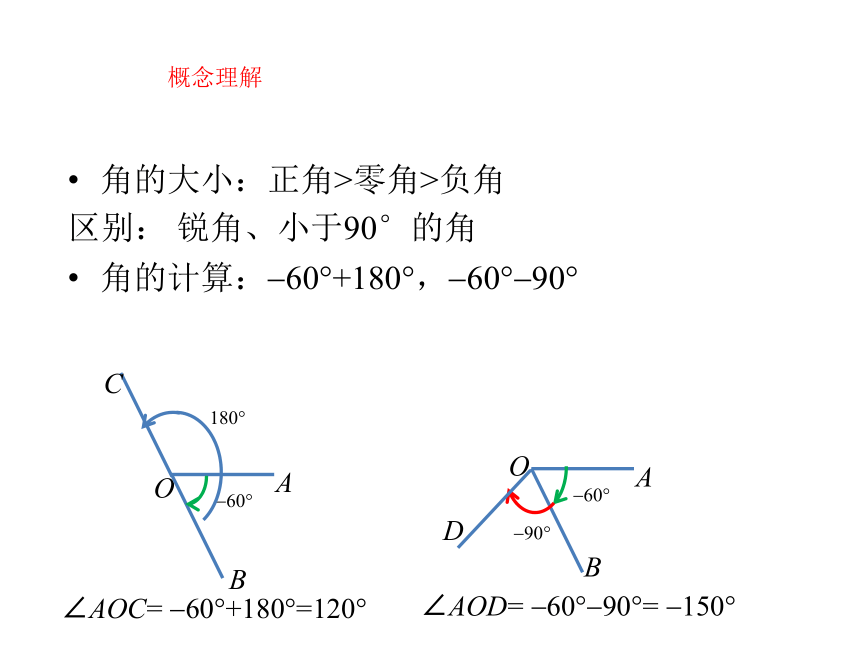
概念理解
角的大小:正角>零角>负角
区别: 锐角、小于90°的角
角的计算:?60?+180?,?60??90?
A
O
?60?
A
O
?60?
180?
B
C
∠AOC= ?60?+180?=120?
B
?90?
D
∠AOD= ?60??90?= ?150?
坐标系中的角
当角的顶点与坐标原点重合,(除顶点外)角的始边落在x轴正半轴上,
根据角的终边的位置分为象限角或轴上角。
角的终边落在第几象限,
就说这个角是第几象限角;
当角的终边与坐标轴重合时,
就说这个角为坐标轴上的角.
y
x
O
概念巩固
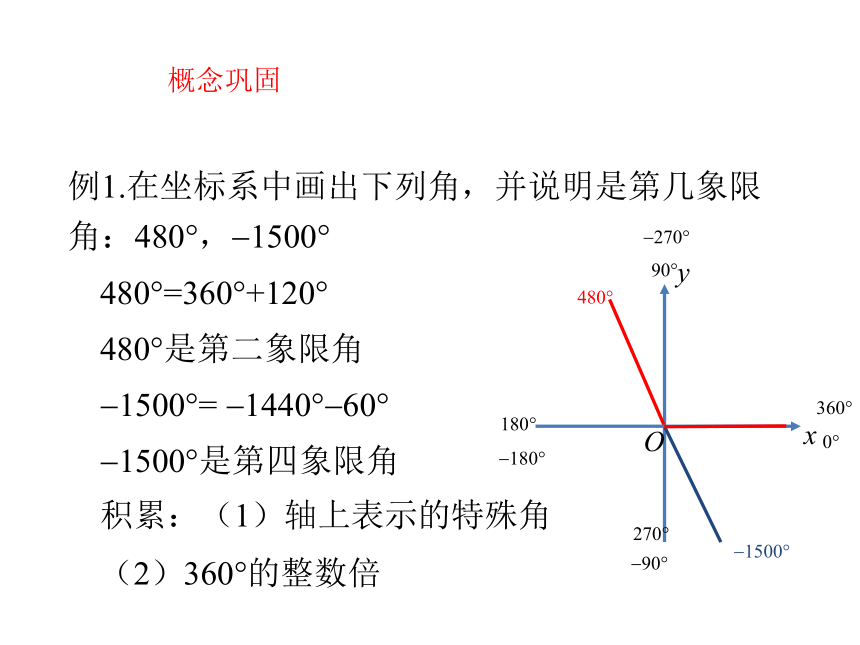
例1.在坐标系中画出下列角,并说明是第几象限角:480?,?1500?
480?=360?+120?
480?是第二象限角
?1500?= ?1440??60?
?1500?是第四象限角
积累:(1)轴上表示的特殊角
(2)360?的整数倍
y
x
O
90?
180?
?90?
0?
360?
?180?
?270?
270?
480?
?1500?
温故知新
练习:在坐标系中画出下列角: 30?, 390?, ?330?, ?690?
390? = 30? + 1 ? 360?
?330? = 30? ? 1 ? 360?
?690? = 30? ? 2 ? 360?
?1050? = 30? ? 3 ? 360?
与30? 终边相同的角
O
表示为? = 30? + k?360? (k?Z)
A
B
30? = 30? + 0 ? 360?
750? = 30? + 2 ? 360?
终边相同的角
与?终边相同的角的集合表示为: { ? | ? = ? + k?360?, k?Z}
(1)角α为任意角;
(2)k∈Z;
(3)k·360°与α之间用“+”号;
(4)终边相同的角不一定相等,但相等的角终边一定相同;
(5)终边相同的角表示不唯一.
? α +k·360°;
α ? k·360°;
知识应用
例2. 与?20?终边相同的角的集合为S
(1) 求S;
(2) 求S中的最小正角;
(3) 求S中满足 ?360?
(4) 若??S,则? +90?,? ?180?是第几象限角?
(1)S={ ? | ? = ?20? + k? 360?, k?Z}
(2)k=1, ? = 340?
(3)k=0,1,2;得 ? = ?20? ,340?,700?
? +90?
? ?180?
(4)? +90?是第一象限角,? ?180?是第二象限角.
知识应用
练习: 写出终边在x轴上的角的集合S
解:与x轴正半轴终边相同的角的集合S1={? | ? = k? 360?, k?Z}
与x轴负半轴终边相同的角的集合S2={? | ? = 180? + k? 360?, k?Z}
S= S1 ∪ S2
注意到k? 360?=2 k?180?, 180? + k? 360?=(2k+1)180?, k?Z,
所以S=S1 ∪ S2 ={? | ? = k? 180?, k?Z}.
知识总结
与?终边相同的角的集合
与?终边共线的角的集合
与?终边垂直的角的集合
终边在坐标轴上的角的集合
{ ? | ? = ? + k?360?, k?Z}
{ ? | ? = ? + k?180?, k?Z}
{? | ? = ?+90? + k? 180?, k?Z}
{ ? | ? = k? 90?, k?Z}
?
?+ 90?
知识应用
例3. 写出下列角的集合为S
(1) 第二象限角
所以S={ ? | 90? + k?360? < ? <180? + k?360?, k?Z }
S={ ? | ? = ? + k?360?, 90? < ? <180? ,k?Z}也对
90?
180?
知识应用
例3. 写出下列角的集合为S
(2) 如图终边在阴影区域
? = 30? + k?360?, k?Z
? = ?120? + k?360?, k?Z
{ ? | 30? + k?360? ? ? ? 240? + k?360?, k?Z }
30?
240?
任意角的概念
与α终边相同的角
象限角、轴上角
小 结
测试反馈
练习1. 已知A={第一象限角},B={锐角},C={小于90?的角},D={正角},写出这几个集合之间的包含关系。
答案:
测试反馈
练习2. 若角α,β的终边相同,则α-β的终边在( )
A.x轴的正半轴
B.y轴的正半轴
C.x轴的负半轴
D.y轴的负半轴
A
测试反馈
练习3. 若α是第三象限角,则 ?α , 180??? 分别是第几象限角?
解:由题180? + k?360? < ? <270? + k?360?, k?Z
所以?180? ? k?360? >?? >?270? ?k?360?, k?Z ,即 ?270? ? k?360? 变形 ?360?+90? ? k?360? 即90? +m?360? 所以??是第二象限角;
由 ?270? ? k?360? 180???是第四象限角。
课后作业
必修三教材
第七页练习A
练习B选做
概念引入
小游戏:将右手臂向右伸直,记该位置为初始位置。
动作1:逆时针旋转90度;
动作2:顺时针旋转270度;
动作3:逆时针旋转一周半。
生活实例
概念形成
任意角的概念:角可以看成平面内一条射线绕着端点
从一个位置旋转到另一个位置所成的图形.
按逆时针方向旋转形成的角叫做正角
按顺时针方向旋转形成的角叫做负角
不作任何旋转形成的角叫做零角
O
A
B
始边OA
终边OB
120°
?240°
概念理解
认识角:390°,?540°
从12点到3点,时针转动______, 分针转过_______.
?1080°
?90°
?
β
概念理解
角的大小:正角>零角>负角
区别: 锐角、小于90°的角
角的计算:?60?+180?,?60??90?
A
O
?60?
A
O
?60?
180?
B
C
∠AOC= ?60?+180?=120?
B
?90?
D
∠AOD= ?60??90?= ?150?
坐标系中的角
当角的顶点与坐标原点重合,(除顶点外)角的始边落在x轴正半轴上,
根据角的终边的位置分为象限角或轴上角。
角的终边落在第几象限,
就说这个角是第几象限角;
当角的终边与坐标轴重合时,
就说这个角为坐标轴上的角.
y
x
O
概念巩固
例1.在坐标系中画出下列角,并说明是第几象限角:480?,?1500?
480?=360?+120?
480?是第二象限角
?1500?= ?1440??60?
?1500?是第四象限角
积累:(1)轴上表示的特殊角
(2)360?的整数倍
y
x
O
90?
180?
?90?
0?
360?
?180?
?270?
270?
480?
?1500?
温故知新
练习:在坐标系中画出下列角: 30?, 390?, ?330?, ?690?
390? = 30? + 1 ? 360?
?330? = 30? ? 1 ? 360?
?690? = 30? ? 2 ? 360?
?1050? = 30? ? 3 ? 360?
与30? 终边相同的角
O
表示为? = 30? + k?360? (k?Z)
A
B
30? = 30? + 0 ? 360?
750? = 30? + 2 ? 360?
终边相同的角
与?终边相同的角的集合表示为: { ? | ? = ? + k?360?, k?Z}
(1)角α为任意角;
(2)k∈Z;
(3)k·360°与α之间用“+”号;
(4)终边相同的角不一定相等,但相等的角终边一定相同;
(5)终边相同的角表示不唯一.
? α +k·360°;
α ? k·360°;
知识应用
例2. 与?20?终边相同的角的集合为S
(1) 求S;
(2) 求S中的最小正角;
(3) 求S中满足 ?360?
(4) 若??S,则? +90?,? ?180?是第几象限角?
(1)S={ ? | ? = ?20? + k? 360?, k?Z}
(2)k=1, ? = 340?
(3)k=0,1,2;得 ? = ?20? ,340?,700?
? +90?
? ?180?
(4)? +90?是第一象限角,? ?180?是第二象限角.
知识应用
练习: 写出终边在x轴上的角的集合S
解:与x轴正半轴终边相同的角的集合S1={? | ? = k? 360?, k?Z}
与x轴负半轴终边相同的角的集合S2={? | ? = 180? + k? 360?, k?Z}
S= S1 ∪ S2
注意到k? 360?=2 k?180?, 180? + k? 360?=(2k+1)180?, k?Z,
所以S=S1 ∪ S2 ={? | ? = k? 180?, k?Z}.
知识总结
与?终边相同的角的集合
与?终边共线的角的集合
与?终边垂直的角的集合
终边在坐标轴上的角的集合
{ ? | ? = ? + k?360?, k?Z}
{ ? | ? = ? + k?180?, k?Z}
{? | ? = ?+90? + k? 180?, k?Z}
{ ? | ? = k? 90?, k?Z}
?
?+ 90?
知识应用
例3. 写出下列角的集合为S
(1) 第二象限角
所以S={ ? | 90? + k?360? < ? <180? + k?360?, k?Z }
S={ ? | ? = ? + k?360?, 90? < ? <180? ,k?Z}也对
90?
180?
知识应用
例3. 写出下列角的集合为S
(2) 如图终边在阴影区域
? = 30? + k?360?, k?Z
? = ?120? + k?360?, k?Z
{ ? | 30? + k?360? ? ? ? 240? + k?360?, k?Z }
30?
240?
任意角的概念
与α终边相同的角
象限角、轴上角
小 结
测试反馈
练习1. 已知A={第一象限角},B={锐角},C={小于90?的角},D={正角},写出这几个集合之间的包含关系。
答案:
测试反馈
练习2. 若角α,β的终边相同,则α-β的终边在( )
A.x轴的正半轴
B.y轴的正半轴
C.x轴的负半轴
D.y轴的负半轴
A
测试反馈
练习3. 若α是第三象限角,则 ?α , 180??? 分别是第几象限角?
解:由题180? + k?360? < ? <270? + k?360?, k?Z
所以?180? ? k?360? >?? >?270? ?k?360?, k?Z ,即 ?270? ? k?360? 变形 ?360?+90? ? k?360? 即90? +m?360? 所以??是第二象限角;
由 ?270? ? k?360? 180???是第四象限角。
课后作业
必修三教材
第七页练习A
练习B选做
