沪教版八年级数学下册22.4 梯形课件 (25张ppt)
文档属性
| 名称 | 沪教版八年级数学下册22.4 梯形课件 (25张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-05 00:00:00 | ||
图片预览




文档简介
(共25张PPT)
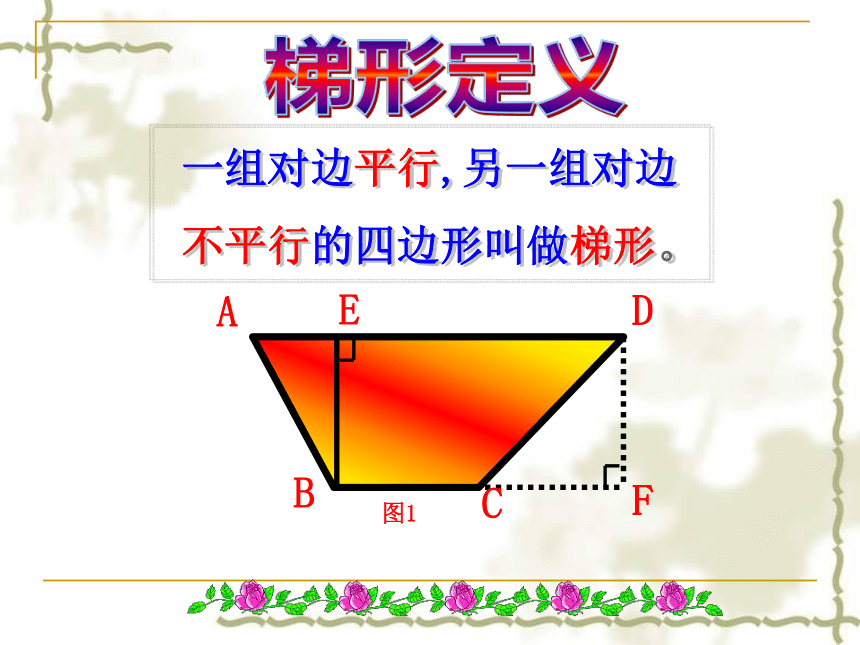
一组对边平行,另一组对边
不平行的四边形叫做梯形。
图1
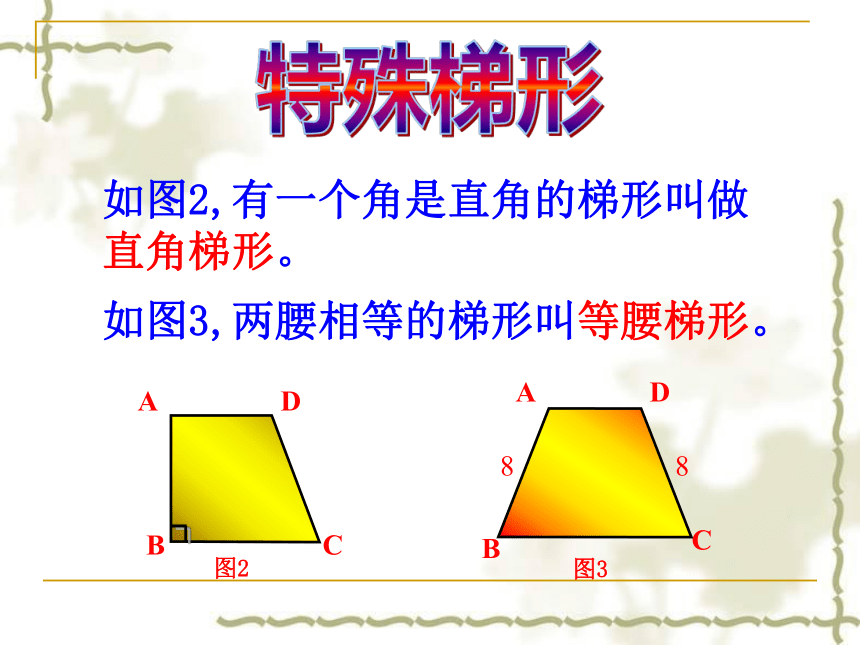
图2
A
B
C
D
图3
A
B
C
D
8
8
图4
A
B
C
D
把你手中的白色等腰梯形纸片沿两底中点所在直线对折。你发现了什么?
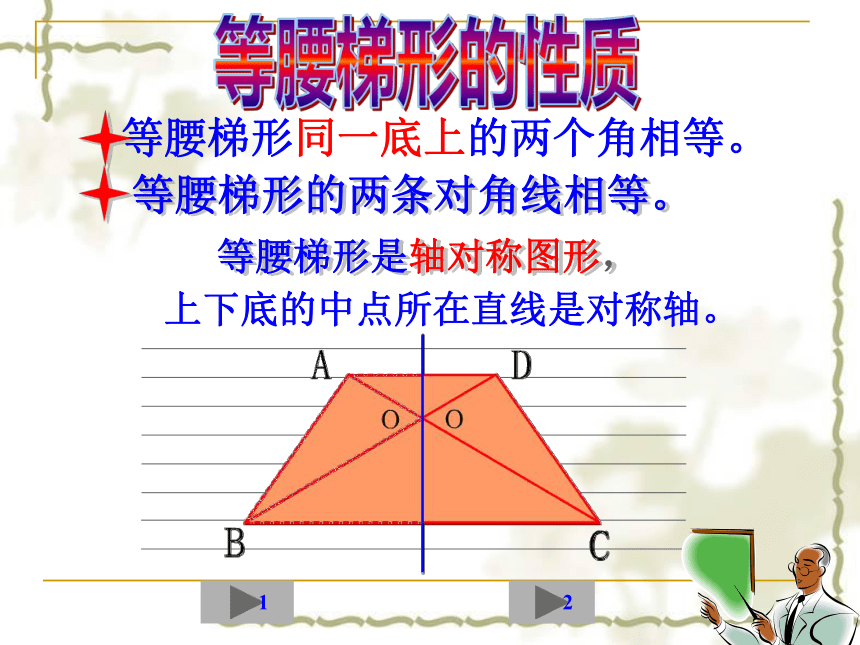
等腰梯形是轴对称图形,
上下底的中点所在直线是对称轴。
1
2
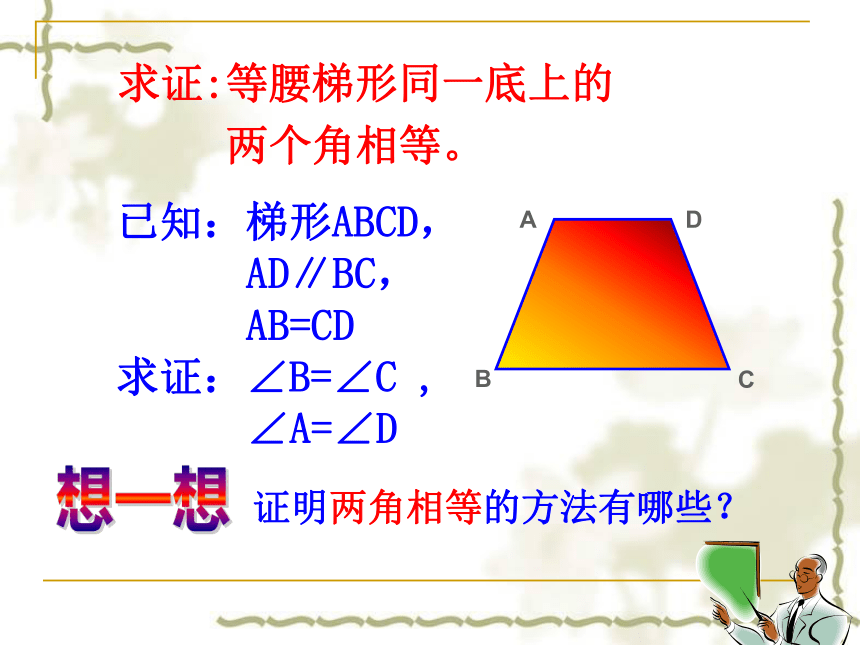
求证:等腰梯形同一底上的
两个角相等。
已知:梯形ABCD,
AD∥BC,
AB=CD
求证:∠B=∠C ,
∠A=∠D
证明两角相等的方法有哪些?
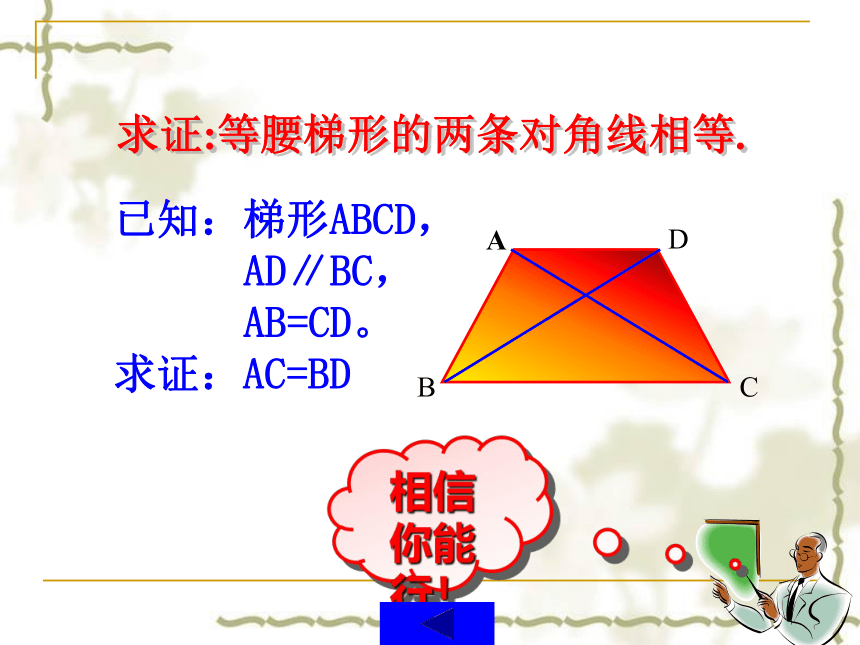
求证:等腰梯形的两条对角线相等.
相信你能行!
已知:梯形ABCD,
AD∥BC,
AB=CD。
求证:AC=BD
1、已知等腰梯形的一个内角等于70°,大家说说其它三个内角的度数是多少。
答:70°,110°,110°。
2、如图5,等腰梯形ABCD中,AD//BC,过点C作对角线BD的平行线CE,交AD延长线于点E,指出图中的平行四边形。并回答:△CAE是等腰三角形吗?为什么?
林州市红旗渠某一段的横截面可近似地看作等腰梯形,如图:测得上口宽为7米,渠底为3米,渠深为3米。求斜坡AB的长。
A
B
C
F
D
A
B
C
F
D
图6
图7
如图8,四边形ABCD是等腰梯形,AD//BC.由四个这样的等腰梯形可以拼出如图9所示的平行四边形。 (1)求四边形ABCD四个内角的度数;
(2)试探究四边形ABCD四条边之间存在的等量关系,并说明理由;
图8
图9
∠A=∠D=120°,∠B=∠C=60°
BC=2AB=2AD=2CD
如图8,四边形ABCD是等腰梯形,AD//BC.由四个这样的等腰梯形可以拼出如图9所示的平行四边形。
(1)求四边形ABCD四个内角的度数;
(2)试探究四边形ABCD四条边之间存在的等量关系,并说明理由;
图8
图9
(3)现有图8中的等腰梯形四个,利用它们你能拼出一个新的等腰梯形吗?若能,四人小组合作拼图,并贴到答题卡背面。
图8
假如你是一位设计师,请选择安阳具有代表性的一处地方(如:火车站,殷墟博物苑,人民公园,市政广场…)进行设计。你准备怎样用这些等腰梯形图案来装扮节日的安阳?
三千多年前的梯形设计
国之瑰宝 司母戊鼎
一千多年前的梯形设计
文峰耸秀 天宁寺塔
三角湖畔 美丽灯展
身边 的 梯 形 设 计
想一想
通过添加辅助线把梯形问题转化成平行四边形和三角形问题来解决。
转化思想
梯形中的数学思想:
已知:梯形ABCD,AD∥BC,把它变成等面积的平行四边形或三角形,在答题卡上画出你的设计方案。
平移腰
平移一条对角线
连结一腰的中点并延长与另一边延长线相交
作梯形的高
多学点
通过本节课的学习,你有
哪些收获?
1、等腰梯形的性质:
(1)同一底上两角相等;
(2)两条对角线相等;
(3)是轴对称图形。
2、梯形中的转化思想:
通过添加辅助线把梯形问题转化 成平行四边形和三角形问题解决。
3、只要我们善于观察,善于思考,合作交 流,用数学的魅力扮世界,世界会更好。
1、
2、
写出本节课的收获
课外探究
①把一个三角形变成和它面积 相等的梯形;
②把一个平行四边形变成和它面积相等的梯形;
③证明等腰梯形是轴对称图形。
生活中并不缺少数学,
缺少的是发现数学的眼睛。
从数学的角度看生活,生活真奇妙。
用数学的魅力扮世界,世界会更好。
一组对边平行,另一组对边
不平行的四边形叫做梯形。
图1
图2
A
B
C
D
图3
A
B
C
D
8
8
图4
A
B
C
D
把你手中的白色等腰梯形纸片沿两底中点所在直线对折。你发现了什么?
等腰梯形是轴对称图形,
上下底的中点所在直线是对称轴。
1
2
求证:等腰梯形同一底上的
两个角相等。
已知:梯形ABCD,
AD∥BC,
AB=CD
求证:∠B=∠C ,
∠A=∠D
证明两角相等的方法有哪些?
求证:等腰梯形的两条对角线相等.
相信你能行!
已知:梯形ABCD,
AD∥BC,
AB=CD。
求证:AC=BD
1、已知等腰梯形的一个内角等于70°,大家说说其它三个内角的度数是多少。
答:70°,110°,110°。
2、如图5,等腰梯形ABCD中,AD//BC,过点C作对角线BD的平行线CE,交AD延长线于点E,指出图中的平行四边形。并回答:△CAE是等腰三角形吗?为什么?
林州市红旗渠某一段的横截面可近似地看作等腰梯形,如图:测得上口宽为7米,渠底为3米,渠深为3米。求斜坡AB的长。
A
B
C
F
D
A
B
C
F
D
图6
图7
如图8,四边形ABCD是等腰梯形,AD//BC.由四个这样的等腰梯形可以拼出如图9所示的平行四边形。 (1)求四边形ABCD四个内角的度数;
(2)试探究四边形ABCD四条边之间存在的等量关系,并说明理由;
图8
图9
∠A=∠D=120°,∠B=∠C=60°
BC=2AB=2AD=2CD
如图8,四边形ABCD是等腰梯形,AD//BC.由四个这样的等腰梯形可以拼出如图9所示的平行四边形。
(1)求四边形ABCD四个内角的度数;
(2)试探究四边形ABCD四条边之间存在的等量关系,并说明理由;
图8
图9
(3)现有图8中的等腰梯形四个,利用它们你能拼出一个新的等腰梯形吗?若能,四人小组合作拼图,并贴到答题卡背面。
图8
假如你是一位设计师,请选择安阳具有代表性的一处地方(如:火车站,殷墟博物苑,人民公园,市政广场…)进行设计。你准备怎样用这些等腰梯形图案来装扮节日的安阳?
三千多年前的梯形设计
国之瑰宝 司母戊鼎
一千多年前的梯形设计
文峰耸秀 天宁寺塔
三角湖畔 美丽灯展
身边 的 梯 形 设 计
想一想
通过添加辅助线把梯形问题转化成平行四边形和三角形问题来解决。
转化思想
梯形中的数学思想:
已知:梯形ABCD,AD∥BC,把它变成等面积的平行四边形或三角形,在答题卡上画出你的设计方案。
平移腰
平移一条对角线
连结一腰的中点并延长与另一边延长线相交
作梯形的高
多学点
通过本节课的学习,你有
哪些收获?
1、等腰梯形的性质:
(1)同一底上两角相等;
(2)两条对角线相等;
(3)是轴对称图形。
2、梯形中的转化思想:
通过添加辅助线把梯形问题转化 成平行四边形和三角形问题解决。
3、只要我们善于观察,善于思考,合作交 流,用数学的魅力扮世界,世界会更好。
1、
2、
写出本节课的收获
课外探究
①把一个三角形变成和它面积 相等的梯形;
②把一个平行四边形变成和它面积相等的梯形;
③证明等腰梯形是轴对称图形。
生活中并不缺少数学,
缺少的是发现数学的眼睛。
从数学的角度看生活,生活真奇妙。
用数学的魅力扮世界,世界会更好。
