人教版高中数学必修四 1.4.3正切函数的性质与图像 课件19PPT
文档属性
| 名称 | 人教版高中数学必修四 1.4.3正切函数的性质与图像 课件19PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 496.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-06 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
1.4.3正切函数的性质与图象
问题1:正切函数的定义域用区间如何表示?
问题2:根据相关诱导公式,你能判断正切函数是周期函数吗?其周期为多少?
所以y=tanx是周期函数, 周期是π.
一.复习旧知,探究新知
问题3:根据相关诱导公式,你能判断正切函数的奇偶性吗?
正切函数是奇函数,图象关于原点对称.
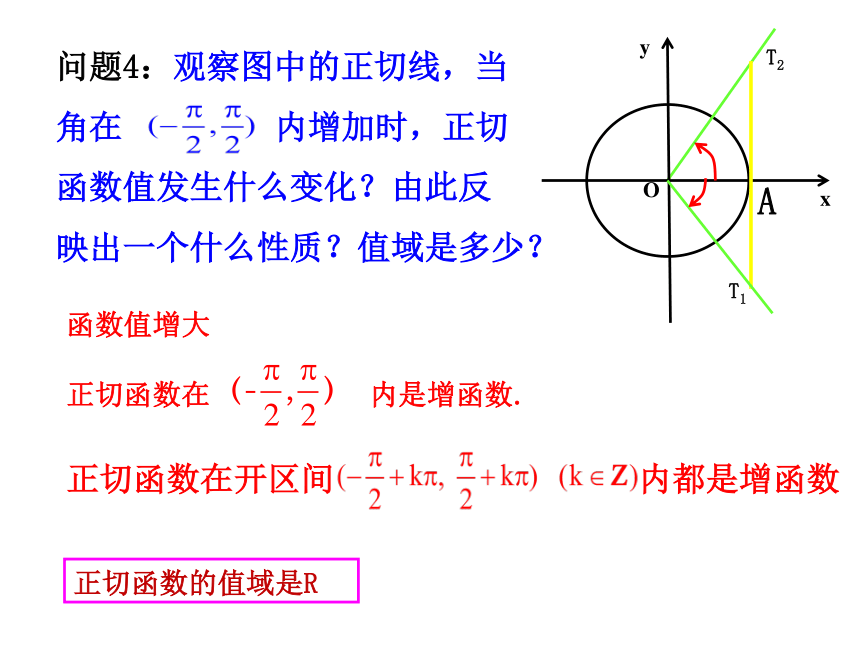
问题4:观察图中的正切线,当
角在 内增加时,正切
函数值发生什么变化?由此反
映出一个什么性质?值域是多少?
函数值增大
正切函数的值域是R
作法:
(1) 等分:
(2) 作正切线;
(3) 平移;
(4) 连线.
把单位圆右半圆分成8等份;
二.探究新知
x
y
1
-1
正切曲线是由被相互平行的直线
所隔开的无穷多支形状相同曲线组成的。
2.根据正切函数的周期性,将图象左、右拓展到 整个定义域内:
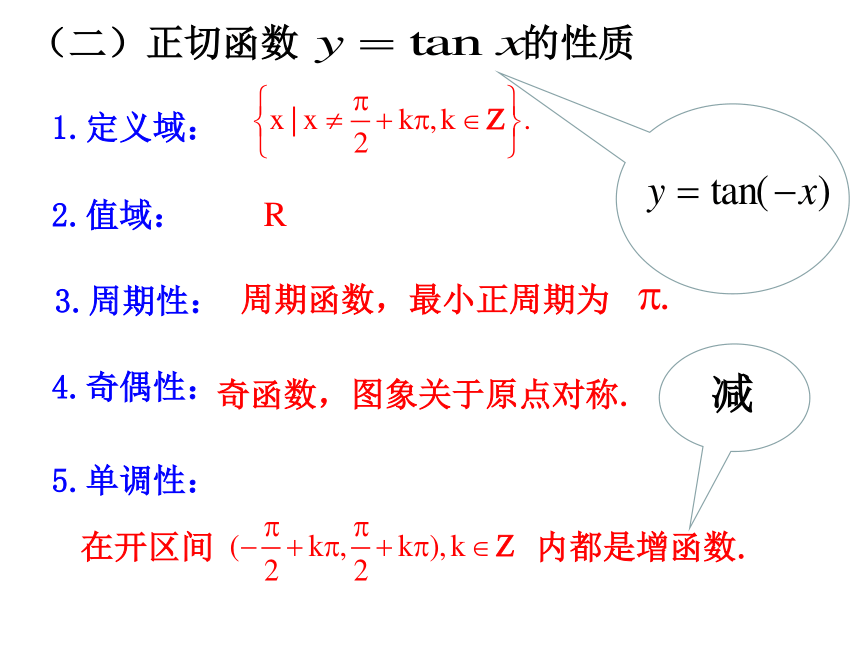
1.定义域:
2.值域:
3.周期性:
5.单调性:
4.奇偶性:
奇函数,图象关于原点对称.
思考:正切函数是整个定义域上的增函数吗?为什么?
不是,
例1.求函数 的定义域、周期和单调区间.
解:函数的自变量x应满足:
即
所以,函数的定义域是:
三.典例分析:
因此函数的周期为2.
解得
因此,函数的单调递增区间是
练习:求函数 的定义域、值域,并指出它的单
调 性.
答案:
1)定义域:
2)值域:
3)周期性:
5)单调性:
4)奇偶性:
奇函数,图象关于原点对称.
四.课堂小结:正切函数的性质与图像
3.思想方法:
数形结合,换元(整体代换),类比,化归.
五.课堂达标:
六.作业布置:
必做:教材 46 页 6 题 , 9 题.
选作:
谢谢大家!
1.4.3正切函数的性质与图象
问题1:正切函数的定义域用区间如何表示?
问题2:根据相关诱导公式,你能判断正切函数是周期函数吗?其周期为多少?
所以y=tanx是周期函数, 周期是π.
一.复习旧知,探究新知
问题3:根据相关诱导公式,你能判断正切函数的奇偶性吗?
正切函数是奇函数,图象关于原点对称.
问题4:观察图中的正切线,当
角在 内增加时,正切
函数值发生什么变化?由此反
映出一个什么性质?值域是多少?
函数值增大
正切函数的值域是R
作法:
(1) 等分:
(2) 作正切线;
(3) 平移;
(4) 连线.
把单位圆右半圆分成8等份;
二.探究新知
x
y
1
-1
正切曲线是由被相互平行的直线
所隔开的无穷多支形状相同曲线组成的。
2.根据正切函数的周期性,将图象左、右拓展到 整个定义域内:
1.定义域:
2.值域:
3.周期性:
5.单调性:
4.奇偶性:
奇函数,图象关于原点对称.
思考:正切函数是整个定义域上的增函数吗?为什么?
不是,
例1.求函数 的定义域、周期和单调区间.
解:函数的自变量x应满足:
即
所以,函数的定义域是:
三.典例分析:
因此函数的周期为2.
解得
因此,函数的单调递增区间是
练习:求函数 的定义域、值域,并指出它的单
调 性.
答案:
1)定义域:
2)值域:
3)周期性:
5)单调性:
4)奇偶性:
奇函数,图象关于原点对称.
四.课堂小结:正切函数的性质与图像
3.思想方法:
数形结合,换元(整体代换),类比,化归.
五.课堂达标:
六.作业布置:
必做:教材 46 页 6 题 , 9 题.
选作:
谢谢大家!
