冀教版八年级数学上册 17.1 等腰三角形 课件 (共23张PPT)
文档属性
| 名称 | 冀教版八年级数学上册 17.1 等腰三角形 课件 (共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-05 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
在我们的身边,许多物体的形状是两边相等的
三角形,如房屋的钢梁架、红领巾、交通标志的外
沿形状等.
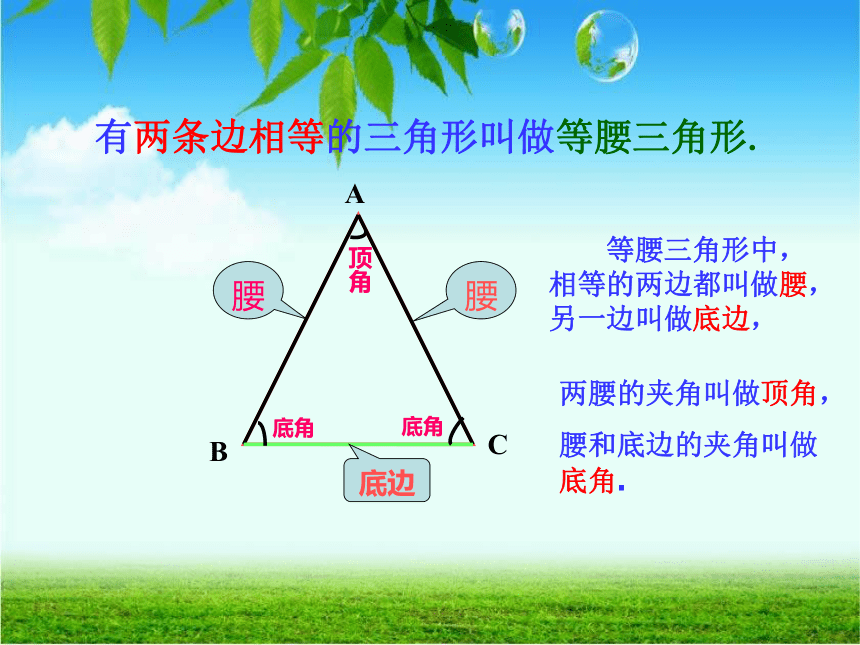
有两条边相等的三角形叫做等腰三角形.
等腰三角形中,相等的两边都叫做腰,另一边叫做底边,
底边
两腰的夹角叫做顶角,
腰和底边的夹角叫做底角.
动手做一做
△ABC有什么特点?
看一看
上述过程中,
剪刀剪过的两条边是相等的,
即△ABC中 AB=AC
∴ △ABC是等腰三角形
1、等腰三角形一腰为3cm,底为4cm,则它的周长
是 ;
10 cm
10 cm 或 11 cm
19 cm
练习
3、等腰三角形的一边长为3cm,另一边长为8cm,则它的周长是 。
2、等腰三角形的一边长为3cm,另一边长为4cm,则它的周长是 ;
探究:
A
C
B
D
AB=AC
BD=CD
AD=AD
∠B = ∠C
∠BAD = ∠CAD
∠ADB = ∠ADC
等腰三角形除了两腰相等以外, 你还能发现其它相等的?
重合的线段 重合的角
猜想与论证一:
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B=?C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
猜想
则有∠1=∠2
D
1
2
在△ABD和△ACD中
证明: 作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等)
则有 BD=CD
D
在△ABD和△ACD中
证明: 作△ABC 的中线AD
AB=AC
BD=CD
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SSS)
∴ ∠B=∠C
(全等三角形对应角相等)
等腰三角形性质
性质1:
等腰三角形两个底角相等,
简称“等边对等角”
在△ABC中,∵ AB=AC
∴ = ,
数学语言
∠B
∠C
A
B
C
⒈ 等腰三角形一个底角为70°,它的另外两个
角为_____ __;
⒉ 等腰三角形一个角为70°,它的另外两个角
为___________________;
70°, 40°
70°,40°或55°,55°
35°,35°
练习
⒊ 等腰三角形一个角为110°,它的另外两个角
为___ __。
如图,已知AB=AC=AD,且AD∥
BC. 求证:∠C=2∠D.
证明:∵AB=AC=AD,
∴∠ABC=∠C,∠ABD=∠D.
∵AD∥BC,∴∠CBD=∠D.
∴∠ABD+∠CBD=2∠D,
即∠ABC=2∠D.∴∠C=2∠D.
A
B
D
C
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB =∠ADC
=90°
重合的线段 重合的角
等腰三角形性质
性质2 等腰三角形的顶角平分线、底边
上的中线、底边上的高互相重合。
(可简记为“三线合一”)
性质2:在△ABC中, ( 1 ) ∵ AB=AC AD是角平分线,
∴ ⊥ , ____=_____ ;
( 2 ) ∵ AB=AC AD是中线,
∴ ⊥ ,∴∠ = ∠____;
( 3 ) ∵ AB=AC AD⊥BC,
∴∠_____=∠______,_____=______ 。
BAD CAD
BAD CAD
AD BC
AD BC
BD CD
BD CD
数学语言
如图,在△ABC中,AB=AC,点D是BC边的中
点,DE,DF分别垂直AB,AC于点E和点F.求证:DE=DF.
证明:如图,连接AD.
∵点D是BC的 中点,
∴AD是△ABC的BC边上的中线
又∵AB=AC,
∴AD平分∠BAC(三线合一).
∵DE,DF分别垂直AB,AC于点E和点F,
∴DE=DF.
等腰三角形是轴对称图形,对称轴是什么?
※等腰三角形是轴对称图形,底边上的中线
(顶角平分线,底边上的高)所在的直线就是
它的对称轴。
关系:特殊的等腰三角形是等边三角形
定义:三边都相等的三角形叫做等边三角形。
下面让我们来证明一下。
等边三角形的性质定理:等边三角形的三个角都相等,并且每一个角都等于60°
已知:在△ABC中, AB=AC=BC
求证:∠A=∠B=∠C
证明:∵ AB=AC
∴ ∠B=∠C
∵AC=BC
∴∠A=∠B
∴∠A=∠B=∠C
∵ ∠A+∠B+∠C=180°
∴∠A=∠B=∠C=60°
A
B
C
例1:已知:如图,在△ABC中, AB = AC,BD,CE
分别为 ∠ABC,∠ACB的平分线.
求证:BD=CE.
证明:∵BD,CE分别为∠ABC,∠ACB的平分线,
∴∠ABC= 2∠ABD,∠ACB= 2∠ACE.
∵∠ABC=∠ACB(等边对等角),
∴∠ABD=∠ACE (等量代换).
∵ AB=AC(已知),∠A=∠A(公共角),
∴△ABD ≌△ACE( ASA).
∴BD=CE(全等三角形的对应边相等).
谈谈你的收获!
等腰三角形是轴对称图形,底边上的中线(顶角平分线,底边上的高)所在的直线就是它的对称轴。
性质1:
等腰三角形两个底角相等,简称“等边对等角”(前提是在同一个三角形中。)
性质2 :
等腰三角形的顶角的顶角平分线、底边上的中线、和底边上的高互相重合,简称“三线合 一”(前提是在同一个等腰三角形中。)
等边三角形的性质定理:等边三角形的三个角都相等,并且每一个角都等于60°。
完成教材P142练习T1-T3,
P143习题A组T1-T4,B组T1-T2
作业:
在我们的身边,许多物体的形状是两边相等的
三角形,如房屋的钢梁架、红领巾、交通标志的外
沿形状等.
有两条边相等的三角形叫做等腰三角形.
等腰三角形中,相等的两边都叫做腰,另一边叫做底边,
底边
两腰的夹角叫做顶角,
腰和底边的夹角叫做底角.
动手做一做
△ABC有什么特点?
看一看
上述过程中,
剪刀剪过的两条边是相等的,
即△ABC中 AB=AC
∴ △ABC是等腰三角形
1、等腰三角形一腰为3cm,底为4cm,则它的周长
是 ;
10 cm
10 cm 或 11 cm
19 cm
练习
3、等腰三角形的一边长为3cm,另一边长为8cm,则它的周长是 。
2、等腰三角形的一边长为3cm,另一边长为4cm,则它的周长是 ;
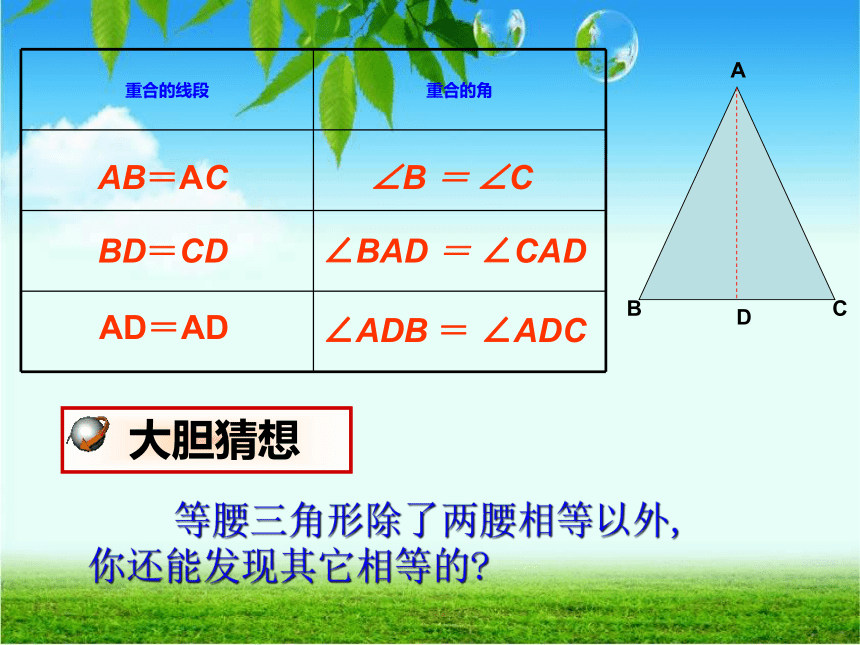
探究:
A
C
B
D
AB=AC
BD=CD
AD=AD
∠B = ∠C
∠BAD = ∠CAD
∠ADB = ∠ADC
等腰三角形除了两腰相等以外, 你还能发现其它相等的?
重合的线段 重合的角
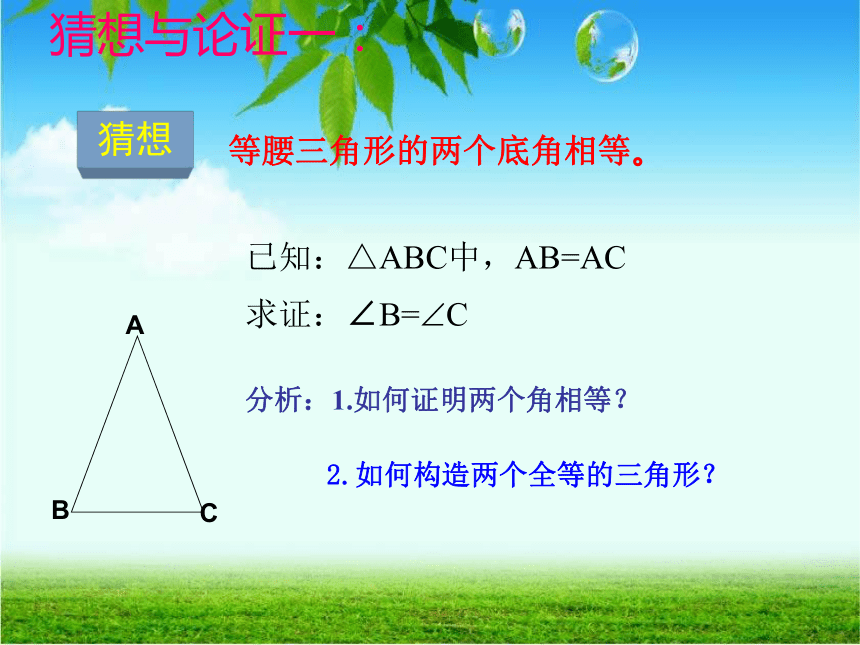
猜想与论证一:
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B=?C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
猜想
则有∠1=∠2
D
1
2
在△ABD和△ACD中
证明: 作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等)
则有 BD=CD
D
在△ABD和△ACD中
证明: 作△ABC 的中线AD
AB=AC
BD=CD
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SSS)
∴ ∠B=∠C
(全等三角形对应角相等)
等腰三角形性质
性质1:
等腰三角形两个底角相等,
简称“等边对等角”
在△ABC中,∵ AB=AC
∴ = ,
数学语言
∠B
∠C
A
B
C
⒈ 等腰三角形一个底角为70°,它的另外两个
角为_____ __;
⒉ 等腰三角形一个角为70°,它的另外两个角
为___________________;
70°, 40°
70°,40°或55°,55°
35°,35°
练习
⒊ 等腰三角形一个角为110°,它的另外两个角
为___ __。
如图,已知AB=AC=AD,且AD∥
BC. 求证:∠C=2∠D.
证明:∵AB=AC=AD,
∴∠ABC=∠C,∠ABD=∠D.
∵AD∥BC,∴∠CBD=∠D.
∴∠ABD+∠CBD=2∠D,
即∠ABC=2∠D.∴∠C=2∠D.
A
B
D
C
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB =∠ADC
=90°
重合的线段 重合的角
等腰三角形性质
性质2 等腰三角形的顶角平分线、底边
上的中线、底边上的高互相重合。
(可简记为“三线合一”)
性质2:在△ABC中, ( 1 ) ∵ AB=AC AD是角平分线,
∴ ⊥ , ____=_____ ;
( 2 ) ∵ AB=AC AD是中线,
∴ ⊥ ,∴∠ = ∠____;
( 3 ) ∵ AB=AC AD⊥BC,
∴∠_____=∠______,_____=______ 。
BAD CAD
BAD CAD
AD BC
AD BC
BD CD
BD CD
数学语言
如图,在△ABC中,AB=AC,点D是BC边的中
点,DE,DF分别垂直AB,AC于点E和点F.求证:DE=DF.
证明:如图,连接AD.
∵点D是BC的 中点,
∴AD是△ABC的BC边上的中线
又∵AB=AC,
∴AD平分∠BAC(三线合一).
∵DE,DF分别垂直AB,AC于点E和点F,
∴DE=DF.
等腰三角形是轴对称图形,对称轴是什么?
※等腰三角形是轴对称图形,底边上的中线
(顶角平分线,底边上的高)所在的直线就是
它的对称轴。
关系:特殊的等腰三角形是等边三角形
定义:三边都相等的三角形叫做等边三角形。
下面让我们来证明一下。
等边三角形的性质定理:等边三角形的三个角都相等,并且每一个角都等于60°
已知:在△ABC中, AB=AC=BC
求证:∠A=∠B=∠C
证明:∵ AB=AC
∴ ∠B=∠C
∵AC=BC
∴∠A=∠B
∴∠A=∠B=∠C
∵ ∠A+∠B+∠C=180°
∴∠A=∠B=∠C=60°
A
B
C
例1:已知:如图,在△ABC中, AB = AC,BD,CE
分别为 ∠ABC,∠ACB的平分线.
求证:BD=CE.
证明:∵BD,CE分别为∠ABC,∠ACB的平分线,
∴∠ABC= 2∠ABD,∠ACB= 2∠ACE.
∵∠ABC=∠ACB(等边对等角),
∴∠ABD=∠ACE (等量代换).
∵ AB=AC(已知),∠A=∠A(公共角),
∴△ABD ≌△ACE( ASA).
∴BD=CE(全等三角形的对应边相等).
谈谈你的收获!
等腰三角形是轴对称图形,底边上的中线(顶角平分线,底边上的高)所在的直线就是它的对称轴。
性质1:
等腰三角形两个底角相等,简称“等边对等角”(前提是在同一个三角形中。)
性质2 :
等腰三角形的顶角的顶角平分线、底边上的中线、和底边上的高互相重合,简称“三线合 一”(前提是在同一个等腰三角形中。)
等边三角形的性质定理:等边三角形的三个角都相等,并且每一个角都等于60°。
完成教材P142练习T1-T3,
P143习题A组T1-T4,B组T1-T2
作业:
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
