人教版八年级数学下册课件:18.2.3正方形的性质课件(共30张PPT)
文档属性
| 名称 | 人教版八年级数学下册课件:18.2.3正方形的性质课件(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-05 13:23:11 | ||
图片预览







文档简介
(共30张PPT)
18.2.3
正方形的性质
人教版八年级下册
学习目标
课堂练习
正方形的定义
正方形的性质
目录
课堂小结
01
学习目标
学习目标:
1. 掌握正方形的定义
2. 掌握正方形的有关性质,并 且要了解正方形与平行四边形,矩形,菱形之间的关系
02
正方形的定义
正方形是我们生活当中最随处可见的形状,正方形的 闹钟 正方形的 烟灰缸 正方形 显示器 正方形的 电源插座盒 正方形的 吊灯 正方形的 记事本 正方形的 纽扣 正方形的 小镜子 正方形的。。。。。。。。。。。等等。。
生活当中的正方形:
怎样用1个长方形纸片折出1个正方形?
怎样将1个菱形木框变成1个正方形木框?
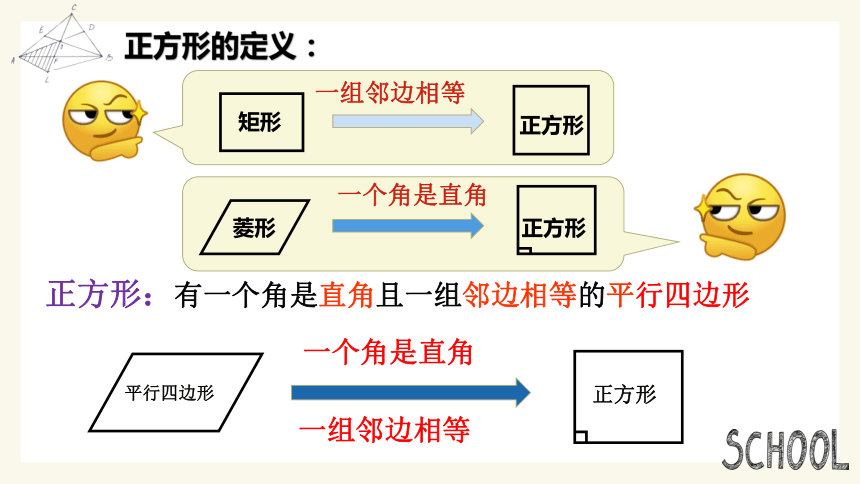
正方形的定义:
一个角是直角
正方形
一组邻边相等
平行四边形
正方形
一个角是直角
菱形
正方形
一组邻边相等
矩形
正方形:有一个角是直角且一组邻边相等的平行四边形
03
正方形的性质
正方形的边
正方形的角
正方形的对角线
A
B
C
D
O
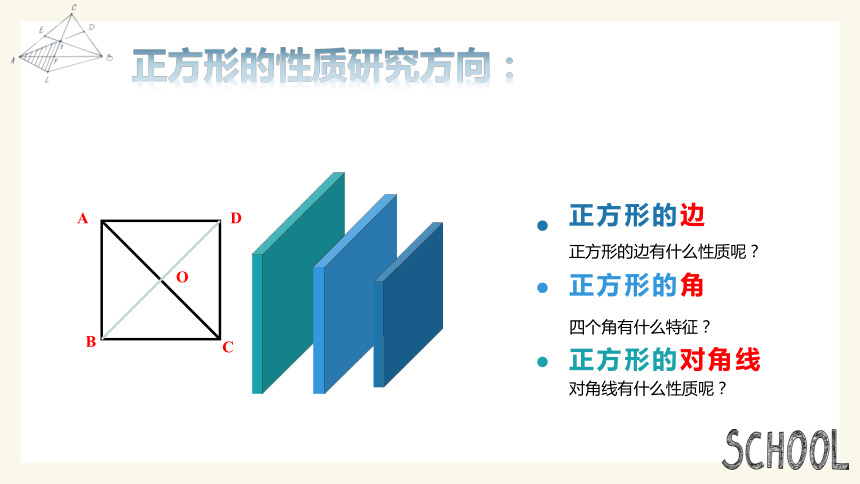
正方形的性质研究方向:
正方形的边有什么性质呢?
四个角有什么特征?
对角线有什么性质呢?
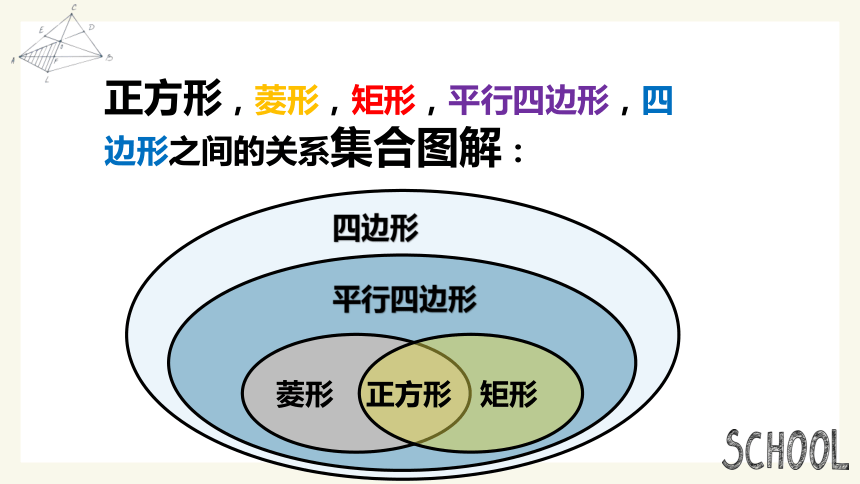
正方形,菱形,矩形,平行四边形,四边形之间的关系集合图解:
平行四边形
菱形
正方形
矩形
四边形
正方形是特殊的矩形,也是特殊的菱形,也是特殊的平行四边形。
正方形的性质=
菱形性质
矩形性质
正方形的边有什么性质呢?
同学们能不能证明呢?
A
B
C
D
O
证明:因为 正方形ABCD是特殊的菱形
所以 AB=BC=CD=AD
AB∥DC,AD∥BC
正方形边的性质:
正方形的四个边都相等
正方形的对边平行
符号语言:
因为 四边形ABCD是正方形
所以 AB=BC=CD=AD
AB∥CD,AD∥BC
正方形的角有什么性质呢?
能不能证明呢?
A
B
C
D
O
证明:因为 正方形ABCD是特殊的矩形
所以 ∠A=∠B=∠C=∠D=90°
正方形角的性质:
正方形的四个角都相等,都是90°
符号语言:
因为 四边形ABCD是正方形
所以 ∠A=∠B=∠C=∠D=90°
正方形的对角线有什么性质呢?
能不能证明呢?
A
B
C
D
O
证明:因为 正方形ABCD是特殊的菱形
所以 AC⊥BD
∠1=∠2,,∠3=∠4, ∠5=∠6,∠7=∠8
又因为 正方形ABCD是特殊的矩形
所以 AC=BD
正方形对角线的性质:
正方形的对角线垂直并且相等,
每条对角线平分每一组对角
符号语言:
因为 四边形ABCD是正方形
所以 AC⊥BD,AC=BD
归纳:
边的性质
角的性质
对角线的性质
正方形
菱形
矩形
平行四边形
四条边相等,对边平行
四个角都是直角
对角线互相垂直且相等
四条边相等,对边平行
对角相等
对角线互相垂直且每一条对角线平分一组对角
对边平行且相等
四个角都是直角
对角线相等
对边平行且相等
对角相等
对角线互相平分
正方形既是轴对称图形又是中心对称图形
正方形对称性的研究:
正方形有几个对称轴?
04
课堂练习
1、周长为20cm的正方形,边长是 对角线长是 面积是 。
3、正方形具有而矩形不一定有的性质是( )
A.四个角是直角 B.对角线互相垂直
C.对角线互相平分 D.对角线相等
4.矩形,菱形,正方形都具有的性质是( )
A.邻边相等 B. 邻角相等
C.对边相等 D. 对角互补
B
5√2
25
8
5
C
2、正方形两条对角线的和为8cm,它的面积为____________.
5.判断以下命题的对错:
1.矩形的对角线相等且互相平分. ( )
2.矩形的对角线相等且互相垂直. ( )
3.菱形的对角线相等且互相平分. ( )
4.菱形的对角线互相垂直且平分. ( )
5.正方形的对角线相等且互相平分. ( )
6.正方形的对角线互相垂直且平分. ( )
7.正方形的对角线相等且互相垂直平分. ( )
√
√
√
√
√
×
×
A
D
C
B
6. 正方形的对角线的长度为8,求正方形的面积
o
解: 对角线×对角线×?
所以 8×8×?=32
这公式又是从哪儿冒出来的呢?
A
D
C
B
o
6. 正方形的对角线的长度为8,求正方形的面积
解: 因为 ABCD是正方形
所以 OA=OB=OC=OD,AC⊥BD
又因为 AC=BD=8
所以OA=OB=OC=OD=4
在Rt△AOB中
矩形,菱形还有这种求面积公式么?
7. AC为正方形ABCD的对角线 , E为AC上一点 , 且AB=AE ,
EF⊥AC交BC于F , 求证:EC=EF=FB .
A
B
C
D
E
F
┌
证明: ∵ 四边形ABCD是正方形 ,
∴∠B=90° , ∠ACB=45° .
∵∠AEF=90° , AB=AE ,
∴△ABF ≌△AFE(HL),
∴BF=EF .
又∵∠FEC=90° ,
∴∠EFC=45°,
∴EC=EF(等角对等边),
∴BF=EF=EC .
8. 如图 , ABCD是一块正方形场地 . 小华和小芳在AB边上取定了一点E ,
测量知 ,EC=30m , EB=10m . 这块场地的面积和对角线分别是多少 ?
解:根据勾股定理:
BC2=EC2-EB2
=302-102
=800 .
∴BC= ,
∴这块场地的面积= =800(m2),
对角线= =40(m) .
?
05
课堂小结
课堂小结:
边的性质
角的性质
对角线的性质
正方形
菱形
矩形
四条边相等,对边平行
四个角都是直角
对角线互相垂直且相等
四条边相等,对边平行
对角相等
对角线互相垂直且每一条对角线平分一组对角
对边平行且相等
四个角都是直角
对角线相等
对边平行且相等
对角相等
对角线互相平分
平行四边形
感谢您的观看
人教版八年级下册
18.2.3
正方形的性质
人教版八年级下册
学习目标
课堂练习
正方形的定义
正方形的性质
目录
课堂小结
01
学习目标
学习目标:
1. 掌握正方形的定义
2. 掌握正方形的有关性质,并 且要了解正方形与平行四边形,矩形,菱形之间的关系
02
正方形的定义
正方形是我们生活当中最随处可见的形状,正方形的 闹钟 正方形的 烟灰缸 正方形 显示器 正方形的 电源插座盒 正方形的 吊灯 正方形的 记事本 正方形的 纽扣 正方形的 小镜子 正方形的。。。。。。。。。。。等等。。
生活当中的正方形:
怎样用1个长方形纸片折出1个正方形?
怎样将1个菱形木框变成1个正方形木框?
正方形的定义:
一个角是直角
正方形
一组邻边相等
平行四边形
正方形
一个角是直角
菱形
正方形
一组邻边相等
矩形
正方形:有一个角是直角且一组邻边相等的平行四边形
03
正方形的性质
正方形的边
正方形的角
正方形的对角线
A
B
C
D
O
正方形的性质研究方向:
正方形的边有什么性质呢?
四个角有什么特征?
对角线有什么性质呢?
正方形,菱形,矩形,平行四边形,四边形之间的关系集合图解:
平行四边形
菱形
正方形
矩形
四边形
正方形是特殊的矩形,也是特殊的菱形,也是特殊的平行四边形。
正方形的性质=
菱形性质
矩形性质
正方形的边有什么性质呢?
同学们能不能证明呢?
A
B
C
D
O
证明:因为 正方形ABCD是特殊的菱形
所以 AB=BC=CD=AD
AB∥DC,AD∥BC
正方形边的性质:
正方形的四个边都相等
正方形的对边平行
符号语言:
因为 四边形ABCD是正方形
所以 AB=BC=CD=AD
AB∥CD,AD∥BC
正方形的角有什么性质呢?
能不能证明呢?
A
B
C
D
O
证明:因为 正方形ABCD是特殊的矩形
所以 ∠A=∠B=∠C=∠D=90°
正方形角的性质:
正方形的四个角都相等,都是90°
符号语言:
因为 四边形ABCD是正方形
所以 ∠A=∠B=∠C=∠D=90°
正方形的对角线有什么性质呢?
能不能证明呢?
A
B
C
D
O
证明:因为 正方形ABCD是特殊的菱形
所以 AC⊥BD
∠1=∠2,,∠3=∠4, ∠5=∠6,∠7=∠8
又因为 正方形ABCD是特殊的矩形
所以 AC=BD
正方形对角线的性质:
正方形的对角线垂直并且相等,
每条对角线平分每一组对角
符号语言:
因为 四边形ABCD是正方形
所以 AC⊥BD,AC=BD
归纳:
边的性质
角的性质
对角线的性质
正方形
菱形
矩形
平行四边形
四条边相等,对边平行
四个角都是直角
对角线互相垂直且相等
四条边相等,对边平行
对角相等
对角线互相垂直且每一条对角线平分一组对角
对边平行且相等
四个角都是直角
对角线相等
对边平行且相等
对角相等
对角线互相平分
正方形既是轴对称图形又是中心对称图形
正方形对称性的研究:
正方形有几个对称轴?
04
课堂练习
1、周长为20cm的正方形,边长是 对角线长是 面积是 。
3、正方形具有而矩形不一定有的性质是( )
A.四个角是直角 B.对角线互相垂直
C.对角线互相平分 D.对角线相等
4.矩形,菱形,正方形都具有的性质是( )
A.邻边相等 B. 邻角相等
C.对边相等 D. 对角互补
B
5√2
25
8
5
C
2、正方形两条对角线的和为8cm,它的面积为____________.
5.判断以下命题的对错:
1.矩形的对角线相等且互相平分. ( )
2.矩形的对角线相等且互相垂直. ( )
3.菱形的对角线相等且互相平分. ( )
4.菱形的对角线互相垂直且平分. ( )
5.正方形的对角线相等且互相平分. ( )
6.正方形的对角线互相垂直且平分. ( )
7.正方形的对角线相等且互相垂直平分. ( )
√
√
√
√
√
×
×
A
D
C
B
6. 正方形的对角线的长度为8,求正方形的面积
o
解: 对角线×对角线×?
所以 8×8×?=32
这公式又是从哪儿冒出来的呢?
A
D
C
B
o
6. 正方形的对角线的长度为8,求正方形的面积
解: 因为 ABCD是正方形
所以 OA=OB=OC=OD,AC⊥BD
又因为 AC=BD=8
所以OA=OB=OC=OD=4
在Rt△AOB中
矩形,菱形还有这种求面积公式么?
7. AC为正方形ABCD的对角线 , E为AC上一点 , 且AB=AE ,
EF⊥AC交BC于F , 求证:EC=EF=FB .
A
B
C
D
E
F
┌
证明: ∵ 四边形ABCD是正方形 ,
∴∠B=90° , ∠ACB=45° .
∵∠AEF=90° , AB=AE ,
∴△ABF ≌△AFE(HL),
∴BF=EF .
又∵∠FEC=90° ,
∴∠EFC=45°,
∴EC=EF(等角对等边),
∴BF=EF=EC .
8. 如图 , ABCD是一块正方形场地 . 小华和小芳在AB边上取定了一点E ,
测量知 ,EC=30m , EB=10m . 这块场地的面积和对角线分别是多少 ?
解:根据勾股定理:
BC2=EC2-EB2
=302-102
=800 .
∴BC= ,
∴这块场地的面积= =800(m2),
对角线= =40(m) .
?
05
课堂小结
课堂小结:
边的性质
角的性质
对角线的性质
正方形
菱形
矩形
四条边相等,对边平行
四个角都是直角
对角线互相垂直且相等
四条边相等,对边平行
对角相等
对角线互相垂直且每一条对角线平分一组对角
对边平行且相等
四个角都是直角
对角线相等
对边平行且相等
对角相等
对角线互相平分
平行四边形
感谢您的观看
人教版八年级下册
