人教版八年级下数学19.2.2一次函数的概念课件(第一课时24张 )
文档属性
| 名称 | 人教版八年级下数学19.2.2一次函数的概念课件(第一课时24张 ) |  | |
| 格式 | zip | ||
| 文件大小 | 793.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-06 15:48:19 | ||
图片预览








文档简介
课件24张PPT。时间是一个常数,但对勤奋者来说,是一“变数”你在学业上的收获与你平时的付出是成正比的。一次函数的概念教学目标
1、经历一般规律的探索过程,发展学生的抽象思维能力。
2、理解一次函数和正比例函数的概念,能根据所给条件写出简单的一次函数表达式,发展学生的数学应用能力。
教学重点
1、 一次函数、正比例函数的概念及两者之间的关系。
2、 会根据已知信息写出一次函数的表达式。
教学难点
一次函数知识的运用教学方法教师引导学生自学。
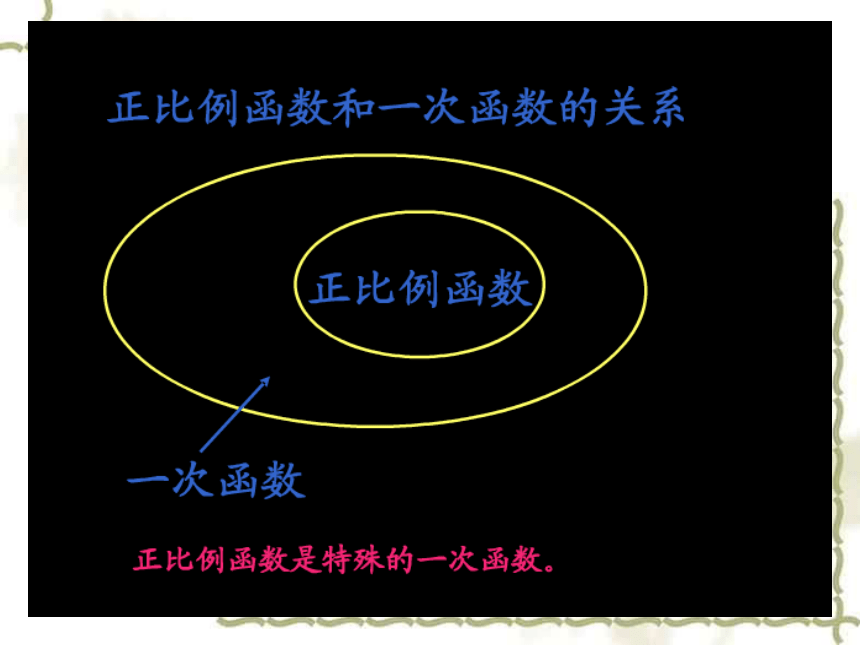
小明暑假第一次去北京.汽车驶上A地的高速公路后,小明观察里程碑,发现汽车的平均速度是95千米/时.已知A地直达北京的高速公路全程570千米,小明想知道汽车从A地驶出后,距北京的路程和汽车在高速公路上行驶的时间有什么关系,以便根据时间估计自己和北京的距离. 问题1 分 析 我们知道汽车距北京的路程随着行车时间而变化.要想找出这两个变化着的量的关系,并据此得出相应的值,显然,应该探究这两个量之间的变化规律.为此,我们设汽车在高速公路上行驶时间为t小时,汽车距北京的路程为s千米,则不难得到s与t的函数关系式是 s=570-95t (1) 问题2 弹簧下端悬挂重物,弹簧会伸长。弹簧的长度y(厘米)是所挂重物质量x(千克)的函数。已知一根弹簧在不挂重物时长6厘米。在一定的弹性限度内,每挂1千克重物弹簧伸长0.3厘米。求这个函数关系式。分 析:因为每挂1千克重物弹簧伸长0.3厘米,所以挂x千克重物时弹簧伸长0.3x厘米,所以挂x千克重物时弹簧的长度为(0.3x+6)厘米,即所求的函数关系式为 y=_______________ (2) 0.3x+6 细心观察:⑴ c = 7t - 35(3) y = 0.01x+22(2) G = h - 1051、在这些函数关系式中,是关于自变量的几次式?2、关于x的一次式的一般形式是什么?(4) y = -5x+ 50 (5) y=0.5x+3 (6) y= -6x+52.y = kx+b分析:1.是关于自变量的一次式.概 括 上述函数的解析式都是用自变量的一次整式表示的函数,我们称它们为一次函数. 一次函数通常可以表示为y=kx+b的形式,其中k、b是常数,k≠0. 特别地,当b=0时,一次函数y=kx(常数k≠0)也叫做正比例函数.正比例函数是一种特殊的一次函数.一次函数定义
它是一次函数.它不是一次函数.它是一次函数,也是正比例函数.它是一次函数.它不是一次函数.它是一次函数.巩固概念练习D2.要使y=(m-2)xn-1+n是关于x的一次函数,n,m应满足 , .n=2m≠23.下列说法不正确的是( )(A)一次函数不一定是正比例函数(B)不是一次函数就一定不是正比例函数(C)正比例函数是特定的一次函数(D)不是正比例函数就不是一次函数D4.若函数y=(m-1)x|m|+m是关于x的一次函数,试求m的值. 1.已知函数y=(m+1)x+(m2-1),当m取什么值时, y是x的一次函数?当m取什么值时,y是x的正比例函数?应用拓展
解:(1)因为y是x的一次函数
所以 m+1 ≠ 0 m≠-1(2)因为y是x的正比例函数
所以 m2-1=0 m=1或-1
又因为 m≠ -1 所以 m=12.已知函数y=(k-2)x+2k+1,若它是一次函数,求k的取值范围;若它是正比例函数,求k的值.解:若y=(k-2)x+2k+1是正比例函数则k=-2k+1=0,k-2≠0, 解得若y=(k-2)x+2k+1是一次函数则k-2≠0, 即k ≠ 23.已知y与x-3成正比例,当x=4时, y=3 .(1)写出y与x之间的函数关系式;(2) y与x之间是什么函数关系式;(3)求x =2.5时, y的值解:(1) ∵ y与x-3成正比例∴可设y = k(x-3)又∵当x=4时, y=3 ∴3 = k(4-3)解得k =3∴y = 3(x-3) = 3x-9(2) y是x的一次函数;(3)当x =2.5时, y = 3×2.5-9 =-1.5(k ≠ 0)4.已知A、B两地相距30千米, B 、C两地相距48千米,某人骑自行车以每小时12千米的速度从A地出发,经过B地到达C地.设此人骑车时间为x(时)离B地距离为y(千米).(1)当此人在A、B两地之间时,求 y与x之间的函数关系式及自变量x的取值范围;(2)当此人在B 、C两地之间时,求 y与x之间的函数关系式及自变量x的取值范围;(1) y=30-12x,(0≤x ≤2.5)(2) y=12x -30,(2.5≤x ≤6.5)略解:分析:5.某油库有一没储油的储油罐,在开始的8分钟内,只开进油管,不开出油管,油罐进油至24吨后,将进油管和出油管同时打开16分钟,油罐中的油从24吨增至40吨.随后又关闭进油管,只开出油管,直至将油罐内的油放完.假设在单位时间内进油管与出油管的流量分别保持不变.写出这段时间内油罐的储油量y(吨)与进出油时间x(分)的函数式及相应的x取值范围.(1)在第一阶段:(0≤x ≤8)24÷8=3解:分析:∴ y= 3x (0≤x ≤8)5.某油库有一没储油的储油罐,在开始的8分钟内,只开进油管,不开出油管,油罐进油至24吨后,将进油管和出油管同时打开16分钟,油罐中的油从24吨增至40吨.随后又关闭进油管,只开出油管,直至将油罐内的油放完.假设在单位时间内进油管与出油管的流量分别保持不变.写出这段时间内油罐的储油量y(吨)与进出油时间x(分)的函数式及相应的x取值范围.(2)在第二阶段:(8≤x ≤8+16)设每分钟放出油m吨,解:∴ y= 24+(3-2)(x-8) (8≤x ≤24)则16×3-16m =40-24m =2即 y= 16+x 5.某油库有一没储油的储油罐,在开始的8分钟内,只开进油管,不开出油管,油罐进油至24吨后,将进油管和出油管同时打开16分钟,油罐中的油从24吨增至40吨.随后又关闭进油管,只开出油管,直至将油罐内的油放完.假设在单位时间内进油管与出油管的流量分别保持不变.写出这段时间内油罐的储油量y(吨)与进出油时间x(分)的函数式及相应的x取值范围.(3)在第三阶段:40÷2=20解:∴ y= 40-2(x-24) (24≤x ≤44)24+20 =44即 y=-2x +88小结 函数的解析式是用自变量的一次整式表示的,我们称它们为一次函数. 一次函数通常可以表示为y=kx+b的形式,其中k、b是常数,k≠0. 正比例函数也是一次函数,它是一次函数的特例. 特别地,当b=0时,一次函数y=kx(常数k≠0)也叫做正比例函数.作业:书上练习及学升配套习题
1、经历一般规律的探索过程,发展学生的抽象思维能力。
2、理解一次函数和正比例函数的概念,能根据所给条件写出简单的一次函数表达式,发展学生的数学应用能力。
教学重点
1、 一次函数、正比例函数的概念及两者之间的关系。
2、 会根据已知信息写出一次函数的表达式。
教学难点
一次函数知识的运用教学方法教师引导学生自学。
小明暑假第一次去北京.汽车驶上A地的高速公路后,小明观察里程碑,发现汽车的平均速度是95千米/时.已知A地直达北京的高速公路全程570千米,小明想知道汽车从A地驶出后,距北京的路程和汽车在高速公路上行驶的时间有什么关系,以便根据时间估计自己和北京的距离. 问题1 分 析 我们知道汽车距北京的路程随着行车时间而变化.要想找出这两个变化着的量的关系,并据此得出相应的值,显然,应该探究这两个量之间的变化规律.为此,我们设汽车在高速公路上行驶时间为t小时,汽车距北京的路程为s千米,则不难得到s与t的函数关系式是 s=570-95t (1) 问题2 弹簧下端悬挂重物,弹簧会伸长。弹簧的长度y(厘米)是所挂重物质量x(千克)的函数。已知一根弹簧在不挂重物时长6厘米。在一定的弹性限度内,每挂1千克重物弹簧伸长0.3厘米。求这个函数关系式。分 析:因为每挂1千克重物弹簧伸长0.3厘米,所以挂x千克重物时弹簧伸长0.3x厘米,所以挂x千克重物时弹簧的长度为(0.3x+6)厘米,即所求的函数关系式为 y=_______________ (2) 0.3x+6 细心观察:⑴ c = 7t - 35(3) y = 0.01x+22(2) G = h - 1051、在这些函数关系式中,是关于自变量的几次式?2、关于x的一次式的一般形式是什么?(4) y = -5x+ 50 (5) y=0.5x+3 (6) y= -6x+52.y = kx+b分析:1.是关于自变量的一次式.概 括 上述函数的解析式都是用自变量的一次整式表示的函数,我们称它们为一次函数. 一次函数通常可以表示为y=kx+b的形式,其中k、b是常数,k≠0. 特别地,当b=0时,一次函数y=kx(常数k≠0)也叫做正比例函数.正比例函数是一种特殊的一次函数.一次函数定义
它是一次函数.它不是一次函数.它是一次函数,也是正比例函数.它是一次函数.它不是一次函数.它是一次函数.巩固概念练习D2.要使y=(m-2)xn-1+n是关于x的一次函数,n,m应满足 , .n=2m≠23.下列说法不正确的是( )(A)一次函数不一定是正比例函数(B)不是一次函数就一定不是正比例函数(C)正比例函数是特定的一次函数(D)不是正比例函数就不是一次函数D4.若函数y=(m-1)x|m|+m是关于x的一次函数,试求m的值. 1.已知函数y=(m+1)x+(m2-1),当m取什么值时, y是x的一次函数?当m取什么值时,y是x的正比例函数?应用拓展
解:(1)因为y是x的一次函数
所以 m+1 ≠ 0 m≠-1(2)因为y是x的正比例函数
所以 m2-1=0 m=1或-1
又因为 m≠ -1 所以 m=12.已知函数y=(k-2)x+2k+1,若它是一次函数,求k的取值范围;若它是正比例函数,求k的值.解:若y=(k-2)x+2k+1是正比例函数则k=-2k+1=0,k-2≠0, 解得若y=(k-2)x+2k+1是一次函数则k-2≠0, 即k ≠ 23.已知y与x-3成正比例,当x=4时, y=3 .(1)写出y与x之间的函数关系式;(2) y与x之间是什么函数关系式;(3)求x =2.5时, y的值解:(1) ∵ y与x-3成正比例∴可设y = k(x-3)又∵当x=4时, y=3 ∴3 = k(4-3)解得k =3∴y = 3(x-3) = 3x-9(2) y是x的一次函数;(3)当x =2.5时, y = 3×2.5-9 =-1.5(k ≠ 0)4.已知A、B两地相距30千米, B 、C两地相距48千米,某人骑自行车以每小时12千米的速度从A地出发,经过B地到达C地.设此人骑车时间为x(时)离B地距离为y(千米).(1)当此人在A、B两地之间时,求 y与x之间的函数关系式及自变量x的取值范围;(2)当此人在B 、C两地之间时,求 y与x之间的函数关系式及自变量x的取值范围;(1) y=30-12x,(0≤x ≤2.5)(2) y=12x -30,(2.5≤x ≤6.5)略解:分析:5.某油库有一没储油的储油罐,在开始的8分钟内,只开进油管,不开出油管,油罐进油至24吨后,将进油管和出油管同时打开16分钟,油罐中的油从24吨增至40吨.随后又关闭进油管,只开出油管,直至将油罐内的油放完.假设在单位时间内进油管与出油管的流量分别保持不变.写出这段时间内油罐的储油量y(吨)与进出油时间x(分)的函数式及相应的x取值范围.(1)在第一阶段:(0≤x ≤8)24÷8=3解:分析:∴ y= 3x (0≤x ≤8)5.某油库有一没储油的储油罐,在开始的8分钟内,只开进油管,不开出油管,油罐进油至24吨后,将进油管和出油管同时打开16分钟,油罐中的油从24吨增至40吨.随后又关闭进油管,只开出油管,直至将油罐内的油放完.假设在单位时间内进油管与出油管的流量分别保持不变.写出这段时间内油罐的储油量y(吨)与进出油时间x(分)的函数式及相应的x取值范围.(2)在第二阶段:(8≤x ≤8+16)设每分钟放出油m吨,解:∴ y= 24+(3-2)(x-8) (8≤x ≤24)则16×3-16m =40-24m =2即 y= 16+x 5.某油库有一没储油的储油罐,在开始的8分钟内,只开进油管,不开出油管,油罐进油至24吨后,将进油管和出油管同时打开16分钟,油罐中的油从24吨增至40吨.随后又关闭进油管,只开出油管,直至将油罐内的油放完.假设在单位时间内进油管与出油管的流量分别保持不变.写出这段时间内油罐的储油量y(吨)与进出油时间x(分)的函数式及相应的x取值范围.(3)在第三阶段:40÷2=20解:∴ y= 40-2(x-24) (24≤x ≤44)24+20 =44即 y=-2x +88小结 函数的解析式是用自变量的一次整式表示的,我们称它们为一次函数. 一次函数通常可以表示为y=kx+b的形式,其中k、b是常数,k≠0. 正比例函数也是一次函数,它是一次函数的特例. 特别地,当b=0时,一次函数y=kx(常数k≠0)也叫做正比例函数.作业:书上练习及学升配套习题
