人教版八年级下数学第十九章 一次函数复习课件(19.1至19.2 共3讲 87张)
文档属性
| 名称 | 人教版八年级下数学第十九章 一次函数复习课件(19.1至19.2 共3讲 87张) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-06 00:00:00 | ||
图片预览









文档简介
课件87张PPT。 静能生慧、静能正道、静能开悟。无事此静坐,一日当两日。静,是一种气质,也是一种修养。诸葛亮云:非淡泊无以明志,非宁静无以致远。唯静才能关照万物,对于所学知识拥有八方联系、浑然一体、漫江碧透、鱼翔浅底的感觉。静是需要锻炼的,古人叫做“习静”。
现在我们开始这样训练自己:
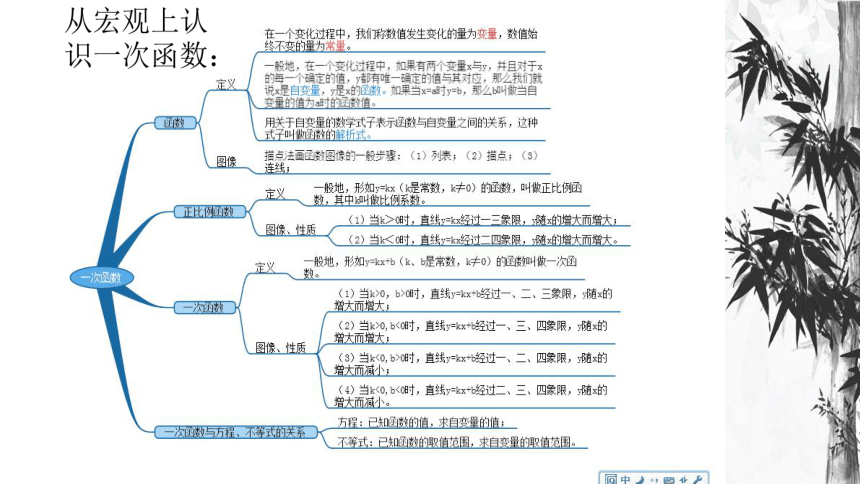
吸气时觉知你在吸气,呼气时觉知你在呼气;深深吸进一口气时,你知道:我正深深地吸进一口气;深深地呼出一口气时,你知道:我正深深地呼出一口气;吸气,让整个呼吸平静下来,你就这样训练自己;呼气,让整个呼吸平静下来,你就这样训练自己。从宏观上认识一次函数:第十九章 一次函数第一讲:
变量与函数:
函数的定义:
函数的表达式:
知识点一常量和变量
在一个变化过程中,我们称数值发生变化的量为变量,数值始终不变的量为常量.
解读 (1)自变量是主动改变的量,而因变量是因为自变量的改变而改变,是被动改变的量.
(2)特别注意“π”是一个无理数,是固定的数值,是常量.知识点一知识点二知识点三知识点四知识点五例1 对于圆的周长公式C=2πR,下列说法正确的是( )
A.π,R是变量,2是常量
B.R是变量,π是常量
C.C是变量,π,R是常量
D.R是变量,2,π是常量
解析改变的是C,R,这两个量是变量;不变的是2和π,这两个量是常量.故选D.
答案D知识点一知识点二知识点三知识点四知识点五知识点一知识点二知识点三知识点四知识点五知识点二函数和自变量
一般地,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值,y都有唯一的值与其对应,那么我们就说x是自变量,y是x的函数.
解读 正确理解函数这一概念必须注意如下几点:
(1)变量x与变量y之间存在的对应关系.例如,y=2x-1
(2)注意理解“x的每一个确定的值”
这句话有两层含义:①自变量x的取值不能使对应关系无意义,如
x的取值不能为1;②自变量x的取值不能使某个变化过程(实际问题)无意义.
(3)自变量x在取值范围内的每一个确定的值,函数y都有一个而且只有一个值与它对应.如y=±x,这里y不是x的函数,因为对于自变量x的每个值,y都有两个值与它对应.
(4)注意正确判断“谁是谁的函数”找准自变量和因变量
知识点一知识点二知识点三知识点四知识点五例2 下列解析式中,y不是x的函数的是 ( )
A.y=-x B.|y|=2x
C.y=|2x| D.y=2x2+4
解析在选项B的关系式|y|=2x中,若x=2,y就有2个值±4与其对应,所以y不是x的函数.故选B.
答案B知识点一知识点二知识点三知识点四知识点五知识点一知识点二知识点三知识点四知识点五知识点三函数值
如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值.
解读 (1)求函数值的一般步骤是:
①代入;②计算求值.
(2)函数值是唯一确定的,但对应的自变量可以是多个.注意以下三点:
①两变量之间的对应关系,同一个自变量对应同一个函数值;
②两个不同的自变量可以对应同一个函数值;
③绝不可以同一个自变量对应两个不同的函数值.知识点一知识点二知识点三知识点四知识点五例3 当x=0时,函数y=2x2+1的值是 ( )
A.1 B.0 C.3 D.-1
解析当x=0时,函数y=2×02+1=1.故选A.
答案A知识点一知识点二知识点三知识点四知识点五知识点一知识点二知识点三知识点四知识点五知识点四函数的解析式
用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数常用的方法,这种式子叫做函数的解析式.
解读 (1)函数的解析式在有的教材中叫做函数表达式、函数关系式.
(2)列解析式时,可以类比列方程,关键是找到其中符合要求的等量关系.
(3)要正确理解函数的解析式,注意以下三点:
①函数的解析式是等式.例如:y=2x+1就是一个函数的解析式,我们可以说代数式2x+1是x的函数,但不能说2x+1是函数的解析式.
②函数的解析式中指明了哪个是自变量,哪个是函数.通常等式右边的代数式中的变量是自变量,等式左边的一个变量表示函数.例如:y=6x2-9中,y是x的函数,x是自变量.知识点一知识点二知识点三知识点四知识点五③书写函数的解析式是有顺序的.例如:y=x-3表示y是x的函数;若x=y+3,则表示x是y的函数.也就是说,求y关于x的函数的解析式,必须用含自变量x的代数式表示y,即得到的等式的左边是一个变量y,右边是一个含x的代数式.知识点一知识点二知识点三知识点四知识点五例4 长方形周长为30 cm,设长为x cm,宽为y cm,则y与x的函数解析式为( )
A.y=30-x B.y=30-2x
C.y=15-x D.y=15+2x
解析∵长方形的周长是30 cm,∴长方形的一组邻边的和为15 cm.∵一边长为x cm,另一边长为y cm,∴y=15-x.故选C.
答案C知识点一知识点二知识点三知识点四知识点五知识点一知识点二知识点三知识点四知识点五知识点五自变量的取值范围
确定自变量的取值范围时,不仅要考虑使函数解析式有意义,而且还要注意问题的实际意义.
解读 (1)自变量的取值范围指的是使自变量有意义的全体.
(2)自变量的取值范围必须使含有自变量的解析式都有意义.通常有以下几种情况:
①当函数的解析式分母不含有自变量时,自变量取全体实数.例知识点一知识点二知识点三知识点四知识点五④当函数的解析式中含有零指整数幂或负整数指数幂时,自变量的取值应使相应的底数不为0.例如,在y=2x0和y=-3x-1中,需要x≠0.
⑤综合型,即解析式右边是由整式、分式、二次根式等综合得到的代数式时,自变量的取值范围是使它们均有意义的公共部分.
⑥对于实际问题中的函数的解析式,自变量的取值除必须使函数的解析式有意义外,还要保证实际问题有意义.例如,人数必须是自然数,长度、面积和体积不能为负数等.知识点一知识点二知识点三知识点四知识点五分析根据所给的式子确定取值范围.
解(1)∵函数的解析式是整式,∴字母的取值没有限制,为全体实数;
(2)∵函数的解析式是分式,∴分母x-1≠0,解得x≠1;
(3)∵函数的解析式是二次根式,∴被开方数4-x≥0,解得x≤4;
(4)由题意,得x-3≥0且x-4≠0,解得x≥3,且x≠4.知识点一知识点二知识点三知识点四知识点五拓展点一拓展点二拓展点三拓展点四拓展点一拓展点二拓展点三拓展点四拓展点一拓展点二拓展点三拓展点四拓展点二根据表格求函数的解析式
例2 婴儿在1到6个月生长发育得非常快,一个婴儿出生时的体重是3 000克,他的体重y(克)与月龄x(月)关系如下:
则y与x的解析式为( )
A.y=x+700 B.y=700x+3 000
C.y=2x+3 000 D.y=5 800-700x
解析∵婴儿出生时的体重是3 000克,每月增长的体重相同为700克,∴体重和月龄的函数解析式为y=700x+3 000.故选B.
答案B拓展点一拓展点二拓展点三拓展点四拓展点一拓展点二拓展点三拓展点四拓展点三根据图形变化求函数的解析式
例3 如图是一组有规律的图案,第(1)个图案由4个基础图形组成,第(2)个图案由7个基础图形组成,…,设第n(n是正整数)个图案由y个基础图形组成,则y与n之间的关系式是( )
A.y=4n B.y=3n
C.y=6n D.y=3n+1拓展点一拓展点二拓展点三拓展点四解析第(1)个图案基础图形的个数为4,
第(2)个图案基础图形的个数为7,7=4+3,
第(3)个图案基础图形的个数为10,10=4+3×2,
…,
第n个图案基础图形的个数为y=4+3(n-1)=3n+1.
故选D.
答案D第十九章 一次函数第一讲内容总结:
变量与函数:变量和常量
函数的定义:函数随自变量的变化而变化,每个 自变量的值对应唯一的函数值
函数的表达式:找到自变量和因变量的关系
第十九章 一次函数19.1.2 函数的图象的定义
函数的表示方法
作函数的图像
知识点一知识点二知识点三知识点四知识点一函数的图象
对于一个函数,把自变量与函数的一一对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
例1 判断点M(2,-1),N(-4,0),Q(1,2)是否在函数y=3x2-2x+1的图象上.
分析把点的坐标代入函数的解析式,看是否满足函数的解析式,如果等号左右两边相等,则该点在函数的图象上,否则就不在.
解将点M(2,-1)中的x=2代入函数y=3x2-2x+1,可得3×22-2×2+1=9≠-1,故点M不在函数的图象上;
将N(-4,0)中的x=-4代入函数y=3x2-2x+1可得:3×(-4)2+8+1≠0,故点N不在函数的图象上.
将Q(1,2)中的x=1代入函数y=3x2-2x+1可得:3×12-2+1=2,故点Q在函数的图象上.知识点一知识点二知识点三知识点四根据函数图像解答问题必备工具一句话解决方案问题模型及类似问题1.横轴、纵轴代表的含义
2.找特殊点
3.数形结合
数形结合,正确理解自变量和函数代表的含义,根据图像变化情况回答例2 如图是某骆驼在两天内的体温变化情况,回答下列问题:
(1)第一天中,骆驼体温的变化范围是什么?它的体温从最低上升到最高需要多少时间?
(2)第二天8时骆驼的体温与第一天8时有什么关系吗?
(3)A点表示的是什么?还有几时的体温与A点所表示的体温相同?根据函数图像解答问题必备工具一句话解决方案问题模型及类似问题1.横轴、纵轴代表的含义
2.找特殊点
3.数形结合
数形结合,正确理解自变量和函数代表的含义,根据图像变化情况回答例2 如图是某骆驼在两天内的体温变化情况,回答下列问题:
知识点二从函数图象读取信息
观察函数图象时,首先要看横轴、纵轴分别代表的是什么,也就是观察图象反映的是哪两个变量之间的关系。 观察图象图象上的特殊点,如与坐标轴的交点、图象上的拐点、线段的端点等,这些特殊点的意义往往对问题的解决有很大的帮助.分析(1)找到第一天中最高点与最低点的坐标,进而可得骆驼体温的变化范围与它的体温从最低上升到最高需要的时间;(2)根据图象找出第一天8时和第二天8时的温度,进行比较即可;(3)根据横、纵坐标的特点得出A点表示的意义,再找出37,44时的体温与A点所表示的体温相同.
根据函数图像解答问题必备工具一句话解决方案问题模型及类似问题1.横轴、纵轴代表的含义
2.找特殊点
3.数形结合
数形结合,正确理解自变量和函数代表的含义,根据图像变化情况回答例2 如图是某骆驼在两天内的体温变化情况,回答下列问题:
解(1)第一天即横坐标在0到24之间,其间最高点的坐标是(12,39),最低点的坐标是(4,35);
故骆驼体温的变化范围是35 ℃~40 ℃,
它的体温从最低上升到最高需要12-4=8(时);
(2)第一天8时骆驼的体温大约是37.5 ℃,第二天8时骆驼的体温大约是36 ℃,从而得出第一天8时比第二天8时的温度高;
(3)A点表示的是第一天12时骆驼的温度是39 ℃,还有大约37时的体温和44时的体温与A点所表示的体温相同.根据函数图像解答问题必备工具一句话解决方案问题模型及类似问题1.横轴、纵轴代表的含义
2.找特殊点
3.数形结合
数形结合,正确理解自变量和函数代表的含义,根据图像变化情况回答拓展点一根据问题情境确定出图象
例1 双流县大林镇“梨乡村雪”远近闻名.家住成都的李明利用星期天开车去大林镇“梨花沟”观赏梨花.
去的过程可用一首小诗来形容:“李明周日看梨花,一早开车离开家,半途没油稍休息,停车以后把油加,愉快到达梨花沟,双流风景美如画.”假设李明保持匀速行驶,用y表示李明行进中离家的距离,用x表示李明离家的时间,下面的图象与小诗的含义大致吻合的是( )根据函数图像解答问题必备工具一句话解决方案问题模型及类似问题1.横轴、纵轴代表的含义
2.找特殊点
3.数形结合
数形结合,正确理解自变量和函数代表的含义,根据图像变化情况回答特殊点:与坐标轴的交点、图象上的拐点、线段的端点
解析汽车由家到加油站这段时间,y随x的增大而增大,是一次函数;在加油站的时间y随x的增大而不变;从加油站到梨花沟这段时间,y随x的增大而增大,与第一段的速度相同.故函数图象是选项B.拓展点一根据问题情境确定出图象
例1李明周日看梨花,一早开车离开家,半途没油稍休息,停车以后把油加,愉快到达梨花沟,双流风景美如画.”假设李明保持匀速行驶,用y表示李明行进中离家的距离,用x表示李明离家的时间,下面的图象与小诗的含义大致吻合的是( )①①①①②②②②根据函数图像解答问题必备工具一句话解决方案问题模型及类似问题1.横轴、纵轴代表的含义
2.找特殊点
3.数形结合
数形结合,正确理解自变量和函数代表的含义,根据图像变化情况回答拓展点二根据图象确定出问题情境
例2 图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x表示时间,y表示张强离家的距离.根据图象提供的信息,以下四个说法错误的是( )
A.体育场离张强家2.5千米
B.张强在体育场锻炼了15分钟
C.体育场离早餐店4千米根据函数图像解答问题必备工具一句话解决方案问题模型及类似问题1.横轴、纵轴代表的含义
2.找特殊点
3.数形结合
数形结合,正确理解自变量和函数代表的含义,根据图像变化情况回答拓展点二根据图象确定出问题情境
例2 图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x表示时间,y表示张强离家的距离.根据图象提供的信息,以下四个说法错误的是( )
A.体育场离张强家2.5千米
B.张强在体育场锻炼了15分钟
C.体育场离早餐店4千米
解析A.由函数图象可知,体育场离张强家2.5千米,故此选项正确;B.由图象可得出张强在体育场锻炼30-15=15(分钟),故此选项正确;C.体育场离张强家2.5千米,体育场离早餐店2.5-1.5=1(千米),故此选项错误;D.∵张强从早餐店回家所用时间为100-65=35(分钟),
/时),故此选项正确.故选C.
②①③根据函数图像解答问题必备工具一句话解决方案问题模型及类似问题1.横轴、纵轴代表的含义
2.找特殊点
3.数形结合
数形结合,正确理解自变量和函数代表的含义,根据图像变化情况回答拓展点三根据图象编写问题情境
例3 在如图所示的三个函数图象中,有两个函数图象能近似地刻画如下a,b两个情境:
情境a:小芳离开家不久,发现把作业本忘在家里,于是返回家里找到了作业本再去学校;
情境b:小芳从家出发,走了一段路程后,为了赶时间,以更快的速度前进.
(1)情境a,b所对应的函数图象分别是 (填写序号);?
(2)请你为剩下的函数图象写出一个适合的情境.根据函数图像解答问题必备工具一句话解决方案问题模型及类似问题1.横轴、纵轴代表的含义
2.找特殊点
3.数形结合
数形结合,正确理解自变量和函数代表的含义,根据图像变化情况回答
分析(1)根据图象,一段一段的分析,再一个一个的排除,即可得出答案;(2)把图象分为三部分,再根据离家的距离进行叙述,即可得出答案.
解(1)情境a:小芳离开家不久,即离家一段路程,此时①②③都符合;发现把作业本忘在家里,于是返回了家里找到了作业本,即又返回家,离家的距离是0,此时②③都符合;又去学校,即离家越来越远,此时只有③返回.∴只有③符合情境a;
情境b:小芳从家出发,走了一段路程后,为了赶时间,以更快的速度前进,即离家越来越远,且没有停留,∴只有①符合.故答案为③①.
(2)情境不唯一.例如:小芳离开家不久,休息了一会儿,又走回了家.知识点一知识点二知识点三知识点四知识点三函数图象的画法
描点法画函数图象的一般步骤如下:
第一步,列表——表中给出一些自变量的值及其对应的函数值;
第二步,描点——在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点;
第三步,连线——按照横坐标由小到大的顺序,把所描出的各点用平滑的曲线连接起来.知识点一知识点二知识点三知识点四解读 (1)列表:列表给出自变量与函数的一些对应值,通常把自变量x的值放在表的第一行,其对应函数值放在第二行,其中x的值从小到大;同时列表时,还应注意自变量的取值范围,取值时可以由小到大,也可以由中间向两边取,根据实际情况,灵活对待.选点应有代表性,不能太少,应尽量使画出的函数图象能反映函数的变化情况.
(2)描点:描点时一般把关键的点准确地描出,取的点越多,画出的图象越准确.
(3)连线:连线时,有时是用线段(直的),有时用平滑的曲线,具体用哪种“线”,要看整个图象的发展趋势,让人感觉过渡自然.知识点一知识点二知识点三知识点四知识点一知识点二知识点三知识点四知识点一知识点二知识点三知识点四知识点一知识点二知识点三知识点四知识点四函数的表示方法
写出函数解析式,或列表格或者画出函数图象,都可以表示具体的函数.这三种表示函数的方法,分别称为解析式法、列表法和图象法.
解读 三种表示方法各有优缺点,应用时要视具体情况,选择适当的表示方法,或将三种方法结合使用.函数三种表示方法的优缺点如下:
(1)解析式法:
优点:简明扼要、规范准确,并且可以根据解析式列表、画图象,进而研究函数的性质;
缺点:有些函数无法写出解析式,只能列出表格或画出图象来表示;知识点一知识点二知识点三知识点四(2)列表法:
优点:能明显地呈现出自变量与对应的函数值;
缺点:取值有限.
(3)图象法:
优点:形象、直观、清晰地呈现出函数的一些性质;
缺点:求得的函数值是近似的.知识点一知识点二知识点三知识点四例4 已知某种型号的摩托车油箱中的剩余油量Q(升)是它行驶时间t(小时)的一次函数.某天老李骑该种摩托车外出旅游,刚开始行驶时,油箱中有油8升,行驶了1小时后,他发现已耗油1.25升.
(1)求油箱中的剩余油量Q(升)与行驶的时间t(小时)的函数解析式,并求出自变量t的取值范围.
(2)在给定的直角坐标系中画出此函数的图象.
(3)从开始行驶算起,如果摩托车以每小时50千米的速度匀速行驶,当油箱中的剩余油量为5.5升时,该摩托车行驶了多少千米?
分析(1)由题意,得Q=-1.25t+8,当Q=0时,t=6.4,得0≤t≤6.4;(2)根据函数的解析式作图;(3)先求出油箱中的剩余油量为5.5升时该摩托车行驶的时间,就可求出路程,路程=速度×时间.知识点一知识点二知识点三知识点四解(1)由题意,得Q=-1.25t+8.
由-1.25t+8=0,得t=6.4.
∴t的取值范围是0≤t≤6.4.
(2)列表:描点、连线,如图所示: 知识点一知识点二知识点三知识点四(3)由5.5=-1.25t+8,得t=2.
∴s=vt=50×2=100.
∴摩托车行驶了100千米.第十九章 一次函数第二讲内容总结:
函数的图象:把自变量与函数的一一对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
函数的表示方法:列表法,图像法,表达式法
作函数的图像:描点、连线
第三讲:正比例函数 研究正比例函数知识点一知识点二知识点三知识点四知识点一正比例函数的由来及定义
列车从哈尔滨出发前往北京,以每小时60千米的速度匀速前进,前进过程中,行驶的时间和路程是什么关系,设行驶时间为X,行驶路程为y,则可以得出
y=60x
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
解读 若某个函数为正比例函数,则可以表示为y=kx(k是常数,k≠0).特别注意,正比例函数中的两个变量的指数都为“1”.
知识点一知识点二知识点三知识点四知识点一知识点二知识点三知识点四知识点一知识点二知识点三知识点四知识点二正比例函数图象的画法
因为两点确定一条直线,所以可用两点法画正比例函数y=kx(k≠0)的图象.一般地,过原点(0,0)和点(1,k)(k是常数,k≠0)的直线,即为正比例函数y=kx(k≠0)的图象.
解读 作正比例函数y=kx(k≠0)的图象时,通常选取(0,0)和(1,k)两点,过这两点作直线即可.但是在实际问题中要注意自变量的取值范围,要灵活选择选取的两点.知识点一知识点二知识点三知识点四例2 在同一直角坐标系中画出下列一次函数的图象:
(1)y=3x;(2)y=5x;(3)y=-5x;(4)y=-3x.
分析根据正比例函数图象的性质可得出它们所经过的两点:原点和(1,k),画图象即可.
解如图所示:
(1)图象过(0,0)和(1,3);
(2)图象过(0,0)和(1,5);
(3)图象过(0,0)和(1,-5);
(4)图象过(0,0)和(1,-3).知识点一知识点二知识点三知识点四知识点一知识点二知识点三知识点四知识点三正比例函数的图象和性质
一般地,正比例函数y=kx(k是常数,k≠0)的图象是一条经过原点的直线,我们称它为直线y=kx.当k>0时,直线y=kx经过第三、第一象限,从左向右上升,即随着x的增大y也增大;当k<0时,直线y=kx经过第二、第四象限,从左向右下降,即随着x的增大y反而减小.
解读 (1)函数的图象“从左向右上升”是指“随着x的增大y也增大”;函数的图象“从左向右下降”是指“随着x的增大y反而减小”.
(2)正比例函数的图象和性质:知识点一知识点二知识点三知识点四例3 下列关于正比例函数y=-5x的说法中,正确的是( )
A.当x=1时,y=5
B.它的图象是一条经过原点的直线
C.y随x的增大而增大
D.它的图象经过第一、三象限
解析A.当x=1时,y=-5,错误;B.正比例函数的图象是一条经过原点的直线,正确;C.根据k<0,得图象经过二、四象限,y随x的增大而减小,错误;D.图象经过第二、四象限,错误.故选B.
答案B知识点一知识点二知识点三知识点四知识点一知识点二知识点三知识点四知识点四确定正比例函数的解析式
确定正比例函数的关系式y=kx(k≠0),实际上就是确定比例系数k(k≠0)的值,一般步骤如下:
(1)先根据条件设出函数解析式为y=kx;
(2)确定一对自变量和函数的对应值(或图象上一个点的坐标);
(3)把对应值代入函数解析式,列出方程,解方程求出k的值;
(4)确定函数解析式.
解读 因为正比例函数的解析式中,只有一个未知字母k,所以只要一个条件就可以确定函数解析式,这个条件可以是图象上一个点的坐标,也可以是一对对应值.知识点一知识点二知识点三知识点四例4 正比例函数如图所示,则这个函数的解析式为( )
A.y=x
B.y=-x
C.y=-2x
解析设这个函数的解析式为y=kx(k≠0),∵函数图象经过(1,-1),
∴-1=k,∴这个函数的解析式为y=-x.故选B.
答案B知识点一知识点二知识点三知识点四拓展点一拓展点二拓展点三拓展点四拓展点五拓展点一根据正比例函数的定义求字母的值
例1 若 是正比例函数,则m的值为( )
A.1 B.-1
解析根据正比例函数的定义,可得2-m2=1,且m-1≠0.∴m=-1.故选B.
答案B拓展点一拓展点二拓展点三拓展点四拓展点五拓展点一拓展点二拓展点三拓展点四拓展点五拓展点三根据正比例函数的性质求字母的取值范围
例3 已知正比例函数y=(k+5)x,且y随x的增大而减小,则k的取值范围是( )
A.k>5 B.k<5
C.k>-5 D.k<-5
解析∵正比例函数y=(k+5)x中若y随x的增大而减小,∴k+5<0.∴k<-5.故选D.
答案D拓展点一拓展点二拓展点三拓展点四拓展点五拓展点一拓展点二拓展点三拓展点四拓展点五拓展点四根据正比例函数的定义和图象求字母的值
例4 正比例函数y=(1-k)x|k-1|的图象经过第二、四象限,那么k的值为( )
A.0 B.-2
C.-1 D.2
解析由题意,得 解得k=2.故选D.
答案D拓展点一拓展点二拓展点三拓展点四拓展点五拓展点一拓展点二拓展点三拓展点四拓展点五拓展点一拓展点二拓展点三拓展点四拓展点五19.2.2 一次函数知识点一知识点二知识点三知识点四知识点五知识点一一次函数的定义
一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数.当b=0时,y=kx+b即为y=kx,所以正比例函数是一种特殊的一次函数.
解读 正比例函数一定是一次函数,是特殊的一次函数,而一次函数包括正比例函数,不一定是正比例函数,只有当b=0时才是正比例函数.知识点一知识点二知识点三知识点四知识点五知识点一知识点二知识点三知识点四知识点五知识点一知识点二知识点三知识点四知识点五知识点二一次函数图象的画法
一次函数y=kx+b(k≠0)图象可以由直线y=kx平移|b|个单位长度得到(当b>0时,向上平移;当b<0时,向下平移).一次函数y=kx+b(k≠0)的图象也是一条直线,我们称为直线y=kx+b.
解读 因为一次函数y=kx+b(k≠0)的图象是一条直线,而两点确定一条直线,这样便可以用两点法来画一次函数的图象.一般地,画正比例函数y=kx(k≠0)的图象,选取(0,0)和(1,k)两点作直线;画一次函数y=kx+b(k≠0)的图象,选取(0,b)和 两点作直线.知识点一知识点二知识点三知识点四知识点五知识点一知识点二知识点三知识点四知识点五分析求出一次函数与x轴、y轴的交点坐标,然后根据两点确定一条直线作出图象即可.
解列表:知识点一知识点二知识点三知识点四知识点五知识点一知识点二知识点三知识点四知识点五知识点一知识点二知识点三知识点四知识点三正比例函数的图象和性质
一般地,正比例函数y=kx(k是常数,k≠0)的图象是一条经过原点的直线,我们称它为直线y=kx.当k>0时,直线y=kx经过第三、第一象限,从左向右上升,即随着x的增大y也增大;当k<0时,直线y=kx经过第二、第四象限,从左向右下降,即随着x的增大y反而减小.
解读 (1)函数的图象“从左向右上升”是指“随着x的增大y也增大”;函数的图象“从左向右下降”是指“随着x的增大y反而减小”.
(2)正比例函数的图象和性质:知识点一知识点二知识点三知识点四知识点五知识点三一次函数的图象和性质
当k>0时,直线y=kx+b从左向右上升;当k<0时,直线y=kx+b从左向右下降.由此可知,一次函数y=kx+b(k,b是常数,k≠0)具有如下性质:
当k>0时,y随x的增大而增大;
当k<0时,y随x的增大而减小.正比例函数的图象和性质:
当k>0时,直线y=kx从左向右上升;当k<0时,直线y=kx从左向右下降.由此可知,一次函数y=kx(k是常数,k≠0)具有如下性质:
当k>0时,y随x的增大而增大;
当k<0时,y随x的增大而减小.
知识点三一次函数的图象和性质
当k>0时,直线y=kx+b从左向右上升;当k<0时,直线y=kx+b从左向右下降.由此可知,一次函数y=kx+b(k,b是常数,k≠0)具有如下性质:
当k>0时,y随x的增大而增大;
当k<0时,y随x的增大而减小.知识点一知识点二知识点三知识点四知识点五例3 已知一次函数y=(2m+1)x+m-3,
(1)若函数图象经过原点,求m的值;
(2)若y随x的增大而增大,求m的取值范围;
(3)一次函数的图象经过第二、三、四象限,求m的取值范围.
分析(1)把点(0,0)代入可求出m的值;(2)根据一次函数的定义及一次函数的增减性列出关于m的不等式,求出m的取值范围;(3)根据题意列出关于m的不等式,求出m的取值范围即可.知识点一知识点二知识点三知识点四知识点五知识点一知识点二知识点三知识点四知识点五
变量与函数:
函数的定义:
函数的表达式:
知识点一常量和变量
在一个变化过程中,我们称数值发生变化的量为变量,数值始终不变的量为常量.
解读 (1)自变量是主动改变的量,而因变量是因为自变量的改变而改变,是被动改变的量.
(2)特别注意“π”是一个无理数,是固定的数值,是常量.知识点一知识点二知识点三知识点四知识点五例1 对于圆的周长公式C=2πR,下列说法正确的是( )
A.π,R是变量,2是常量
B.R是变量,π是常量
C.C是变量,π,R是常量
D.R是变量,2,π是常量
解析改变的是C,R,这两个量是变量;不变的是2和π,这两个量是常量.故选D.
答案D知识点一知识点二知识点三知识点四知识点五知识点一知识点二知识点三知识点四知识点五知识点二函数和自变量
一般地,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值,y都有唯一的值与其对应,那么我们就说x是自变量,y是x的函数.
解读 正确理解函数这一概念必须注意如下几点:
(1)变量x与变量y之间存在的对应关系.例如,y=2x-1
(2)注意理解“x的每一个确定的值”
这句话有两层含义:①自变量x的取值不能使对应关系无意义,如
x的取值不能为1;②自变量x的取值不能使某个变化过程(实际问题)无意义.
(3)自变量x在取值范围内的每一个确定的值,函数y都有一个而且只有一个值与它对应.如y=±x,这里y不是x的函数,因为对于自变量x的每个值,y都有两个值与它对应.
(4)注意正确判断“谁是谁的函数”找准自变量和因变量
知识点一知识点二知识点三知识点四知识点五例2 下列解析式中,y不是x的函数的是 ( )
A.y=-x B.|y|=2x
C.y=|2x| D.y=2x2+4
解析在选项B的关系式|y|=2x中,若x=2,y就有2个值±4与其对应,所以y不是x的函数.故选B.
答案B知识点一知识点二知识点三知识点四知识点五知识点一知识点二知识点三知识点四知识点五知识点三函数值
如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值.
解读 (1)求函数值的一般步骤是:
①代入;②计算求值.
(2)函数值是唯一确定的,但对应的自变量可以是多个.注意以下三点:
①两变量之间的对应关系,同一个自变量对应同一个函数值;
②两个不同的自变量可以对应同一个函数值;
③绝不可以同一个自变量对应两个不同的函数值.知识点一知识点二知识点三知识点四知识点五例3 当x=0时,函数y=2x2+1的值是 ( )
A.1 B.0 C.3 D.-1
解析当x=0时,函数y=2×02+1=1.故选A.
答案A知识点一知识点二知识点三知识点四知识点五知识点一知识点二知识点三知识点四知识点五知识点四函数的解析式
用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数常用的方法,这种式子叫做函数的解析式.
解读 (1)函数的解析式在有的教材中叫做函数表达式、函数关系式.
(2)列解析式时,可以类比列方程,关键是找到其中符合要求的等量关系.
(3)要正确理解函数的解析式,注意以下三点:
①函数的解析式是等式.例如:y=2x+1就是一个函数的解析式,我们可以说代数式2x+1是x的函数,但不能说2x+1是函数的解析式.
②函数的解析式中指明了哪个是自变量,哪个是函数.通常等式右边的代数式中的变量是自变量,等式左边的一个变量表示函数.例如:y=6x2-9中,y是x的函数,x是自变量.知识点一知识点二知识点三知识点四知识点五③书写函数的解析式是有顺序的.例如:y=x-3表示y是x的函数;若x=y+3,则表示x是y的函数.也就是说,求y关于x的函数的解析式,必须用含自变量x的代数式表示y,即得到的等式的左边是一个变量y,右边是一个含x的代数式.知识点一知识点二知识点三知识点四知识点五例4 长方形周长为30 cm,设长为x cm,宽为y cm,则y与x的函数解析式为( )
A.y=30-x B.y=30-2x
C.y=15-x D.y=15+2x
解析∵长方形的周长是30 cm,∴长方形的一组邻边的和为15 cm.∵一边长为x cm,另一边长为y cm,∴y=15-x.故选C.
答案C知识点一知识点二知识点三知识点四知识点五知识点一知识点二知识点三知识点四知识点五知识点五自变量的取值范围
确定自变量的取值范围时,不仅要考虑使函数解析式有意义,而且还要注意问题的实际意义.
解读 (1)自变量的取值范围指的是使自变量有意义的全体.
(2)自变量的取值范围必须使含有自变量的解析式都有意义.通常有以下几种情况:
①当函数的解析式分母不含有自变量时,自变量取全体实数.例知识点一知识点二知识点三知识点四知识点五④当函数的解析式中含有零指整数幂或负整数指数幂时,自变量的取值应使相应的底数不为0.例如,在y=2x0和y=-3x-1中,需要x≠0.
⑤综合型,即解析式右边是由整式、分式、二次根式等综合得到的代数式时,自变量的取值范围是使它们均有意义的公共部分.
⑥对于实际问题中的函数的解析式,自变量的取值除必须使函数的解析式有意义外,还要保证实际问题有意义.例如,人数必须是自然数,长度、面积和体积不能为负数等.知识点一知识点二知识点三知识点四知识点五分析根据所给的式子确定取值范围.
解(1)∵函数的解析式是整式,∴字母的取值没有限制,为全体实数;
(2)∵函数的解析式是分式,∴分母x-1≠0,解得x≠1;
(3)∵函数的解析式是二次根式,∴被开方数4-x≥0,解得x≤4;
(4)由题意,得x-3≥0且x-4≠0,解得x≥3,且x≠4.知识点一知识点二知识点三知识点四知识点五拓展点一拓展点二拓展点三拓展点四拓展点一拓展点二拓展点三拓展点四拓展点一拓展点二拓展点三拓展点四拓展点二根据表格求函数的解析式
例2 婴儿在1到6个月生长发育得非常快,一个婴儿出生时的体重是3 000克,他的体重y(克)与月龄x(月)关系如下:
则y与x的解析式为( )
A.y=x+700 B.y=700x+3 000
C.y=2x+3 000 D.y=5 800-700x
解析∵婴儿出生时的体重是3 000克,每月增长的体重相同为700克,∴体重和月龄的函数解析式为y=700x+3 000.故选B.
答案B拓展点一拓展点二拓展点三拓展点四拓展点一拓展点二拓展点三拓展点四拓展点三根据图形变化求函数的解析式
例3 如图是一组有规律的图案,第(1)个图案由4个基础图形组成,第(2)个图案由7个基础图形组成,…,设第n(n是正整数)个图案由y个基础图形组成,则y与n之间的关系式是( )
A.y=4n B.y=3n
C.y=6n D.y=3n+1拓展点一拓展点二拓展点三拓展点四解析第(1)个图案基础图形的个数为4,
第(2)个图案基础图形的个数为7,7=4+3,
第(3)个图案基础图形的个数为10,10=4+3×2,
…,
第n个图案基础图形的个数为y=4+3(n-1)=3n+1.
故选D.
答案D第十九章 一次函数第一讲内容总结:
变量与函数:变量和常量
函数的定义:函数随自变量的变化而变化,每个 自变量的值对应唯一的函数值
函数的表达式:找到自变量和因变量的关系
第十九章 一次函数19.1.2 函数的图象的定义
函数的表示方法
作函数的图像
知识点一知识点二知识点三知识点四知识点一函数的图象
对于一个函数,把自变量与函数的一一对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
例1 判断点M(2,-1),N(-4,0),Q(1,2)是否在函数y=3x2-2x+1的图象上.
分析把点的坐标代入函数的解析式,看是否满足函数的解析式,如果等号左右两边相等,则该点在函数的图象上,否则就不在.
解将点M(2,-1)中的x=2代入函数y=3x2-2x+1,可得3×22-2×2+1=9≠-1,故点M不在函数的图象上;
将N(-4,0)中的x=-4代入函数y=3x2-2x+1可得:3×(-4)2+8+1≠0,故点N不在函数的图象上.
将Q(1,2)中的x=1代入函数y=3x2-2x+1可得:3×12-2+1=2,故点Q在函数的图象上.知识点一知识点二知识点三知识点四根据函数图像解答问题必备工具一句话解决方案问题模型及类似问题1.横轴、纵轴代表的含义
2.找特殊点
3.数形结合
数形结合,正确理解自变量和函数代表的含义,根据图像变化情况回答例2 如图是某骆驼在两天内的体温变化情况,回答下列问题:
(1)第一天中,骆驼体温的变化范围是什么?它的体温从最低上升到最高需要多少时间?
(2)第二天8时骆驼的体温与第一天8时有什么关系吗?
(3)A点表示的是什么?还有几时的体温与A点所表示的体温相同?根据函数图像解答问题必备工具一句话解决方案问题模型及类似问题1.横轴、纵轴代表的含义
2.找特殊点
3.数形结合
数形结合,正确理解自变量和函数代表的含义,根据图像变化情况回答例2 如图是某骆驼在两天内的体温变化情况,回答下列问题:
知识点二从函数图象读取信息
观察函数图象时,首先要看横轴、纵轴分别代表的是什么,也就是观察图象反映的是哪两个变量之间的关系。 观察图象图象上的特殊点,如与坐标轴的交点、图象上的拐点、线段的端点等,这些特殊点的意义往往对问题的解决有很大的帮助.分析(1)找到第一天中最高点与最低点的坐标,进而可得骆驼体温的变化范围与它的体温从最低上升到最高需要的时间;(2)根据图象找出第一天8时和第二天8时的温度,进行比较即可;(3)根据横、纵坐标的特点得出A点表示的意义,再找出37,44时的体温与A点所表示的体温相同.
根据函数图像解答问题必备工具一句话解决方案问题模型及类似问题1.横轴、纵轴代表的含义
2.找特殊点
3.数形结合
数形结合,正确理解自变量和函数代表的含义,根据图像变化情况回答例2 如图是某骆驼在两天内的体温变化情况,回答下列问题:
解(1)第一天即横坐标在0到24之间,其间最高点的坐标是(12,39),最低点的坐标是(4,35);
故骆驼体温的变化范围是35 ℃~40 ℃,
它的体温从最低上升到最高需要12-4=8(时);
(2)第一天8时骆驼的体温大约是37.5 ℃,第二天8时骆驼的体温大约是36 ℃,从而得出第一天8时比第二天8时的温度高;
(3)A点表示的是第一天12时骆驼的温度是39 ℃,还有大约37时的体温和44时的体温与A点所表示的体温相同.根据函数图像解答问题必备工具一句话解决方案问题模型及类似问题1.横轴、纵轴代表的含义
2.找特殊点
3.数形结合
数形结合,正确理解自变量和函数代表的含义,根据图像变化情况回答拓展点一根据问题情境确定出图象
例1 双流县大林镇“梨乡村雪”远近闻名.家住成都的李明利用星期天开车去大林镇“梨花沟”观赏梨花.
去的过程可用一首小诗来形容:“李明周日看梨花,一早开车离开家,半途没油稍休息,停车以后把油加,愉快到达梨花沟,双流风景美如画.”假设李明保持匀速行驶,用y表示李明行进中离家的距离,用x表示李明离家的时间,下面的图象与小诗的含义大致吻合的是( )根据函数图像解答问题必备工具一句话解决方案问题模型及类似问题1.横轴、纵轴代表的含义
2.找特殊点
3.数形结合
数形结合,正确理解自变量和函数代表的含义,根据图像变化情况回答特殊点:与坐标轴的交点、图象上的拐点、线段的端点
解析汽车由家到加油站这段时间,y随x的增大而增大,是一次函数;在加油站的时间y随x的增大而不变;从加油站到梨花沟这段时间,y随x的增大而增大,与第一段的速度相同.故函数图象是选项B.拓展点一根据问题情境确定出图象
例1李明周日看梨花,一早开车离开家,半途没油稍休息,停车以后把油加,愉快到达梨花沟,双流风景美如画.”假设李明保持匀速行驶,用y表示李明行进中离家的距离,用x表示李明离家的时间,下面的图象与小诗的含义大致吻合的是( )①①①①②②②②根据函数图像解答问题必备工具一句话解决方案问题模型及类似问题1.横轴、纵轴代表的含义
2.找特殊点
3.数形结合
数形结合,正确理解自变量和函数代表的含义,根据图像变化情况回答拓展点二根据图象确定出问题情境
例2 图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x表示时间,y表示张强离家的距离.根据图象提供的信息,以下四个说法错误的是( )
A.体育场离张强家2.5千米
B.张强在体育场锻炼了15分钟
C.体育场离早餐店4千米根据函数图像解答问题必备工具一句话解决方案问题模型及类似问题1.横轴、纵轴代表的含义
2.找特殊点
3.数形结合
数形结合,正确理解自变量和函数代表的含义,根据图像变化情况回答拓展点二根据图象确定出问题情境
例2 图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x表示时间,y表示张强离家的距离.根据图象提供的信息,以下四个说法错误的是( )
A.体育场离张强家2.5千米
B.张强在体育场锻炼了15分钟
C.体育场离早餐店4千米
解析A.由函数图象可知,体育场离张强家2.5千米,故此选项正确;B.由图象可得出张强在体育场锻炼30-15=15(分钟),故此选项正确;C.体育场离张强家2.5千米,体育场离早餐店2.5-1.5=1(千米),故此选项错误;D.∵张强从早餐店回家所用时间为100-65=35(分钟),
/时),故此选项正确.故选C.
②①③根据函数图像解答问题必备工具一句话解决方案问题模型及类似问题1.横轴、纵轴代表的含义
2.找特殊点
3.数形结合
数形结合,正确理解自变量和函数代表的含义,根据图像变化情况回答拓展点三根据图象编写问题情境
例3 在如图所示的三个函数图象中,有两个函数图象能近似地刻画如下a,b两个情境:
情境a:小芳离开家不久,发现把作业本忘在家里,于是返回家里找到了作业本再去学校;
情境b:小芳从家出发,走了一段路程后,为了赶时间,以更快的速度前进.
(1)情境a,b所对应的函数图象分别是 (填写序号);?
(2)请你为剩下的函数图象写出一个适合的情境.根据函数图像解答问题必备工具一句话解决方案问题模型及类似问题1.横轴、纵轴代表的含义
2.找特殊点
3.数形结合
数形结合,正确理解自变量和函数代表的含义,根据图像变化情况回答
分析(1)根据图象,一段一段的分析,再一个一个的排除,即可得出答案;(2)把图象分为三部分,再根据离家的距离进行叙述,即可得出答案.
解(1)情境a:小芳离开家不久,即离家一段路程,此时①②③都符合;发现把作业本忘在家里,于是返回了家里找到了作业本,即又返回家,离家的距离是0,此时②③都符合;又去学校,即离家越来越远,此时只有③返回.∴只有③符合情境a;
情境b:小芳从家出发,走了一段路程后,为了赶时间,以更快的速度前进,即离家越来越远,且没有停留,∴只有①符合.故答案为③①.
(2)情境不唯一.例如:小芳离开家不久,休息了一会儿,又走回了家.知识点一知识点二知识点三知识点四知识点三函数图象的画法
描点法画函数图象的一般步骤如下:
第一步,列表——表中给出一些自变量的值及其对应的函数值;
第二步,描点——在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点;
第三步,连线——按照横坐标由小到大的顺序,把所描出的各点用平滑的曲线连接起来.知识点一知识点二知识点三知识点四解读 (1)列表:列表给出自变量与函数的一些对应值,通常把自变量x的值放在表的第一行,其对应函数值放在第二行,其中x的值从小到大;同时列表时,还应注意自变量的取值范围,取值时可以由小到大,也可以由中间向两边取,根据实际情况,灵活对待.选点应有代表性,不能太少,应尽量使画出的函数图象能反映函数的变化情况.
(2)描点:描点时一般把关键的点准确地描出,取的点越多,画出的图象越准确.
(3)连线:连线时,有时是用线段(直的),有时用平滑的曲线,具体用哪种“线”,要看整个图象的发展趋势,让人感觉过渡自然.知识点一知识点二知识点三知识点四知识点一知识点二知识点三知识点四知识点一知识点二知识点三知识点四知识点一知识点二知识点三知识点四知识点四函数的表示方法
写出函数解析式,或列表格或者画出函数图象,都可以表示具体的函数.这三种表示函数的方法,分别称为解析式法、列表法和图象法.
解读 三种表示方法各有优缺点,应用时要视具体情况,选择适当的表示方法,或将三种方法结合使用.函数三种表示方法的优缺点如下:
(1)解析式法:
优点:简明扼要、规范准确,并且可以根据解析式列表、画图象,进而研究函数的性质;
缺点:有些函数无法写出解析式,只能列出表格或画出图象来表示;知识点一知识点二知识点三知识点四(2)列表法:
优点:能明显地呈现出自变量与对应的函数值;
缺点:取值有限.
(3)图象法:
优点:形象、直观、清晰地呈现出函数的一些性质;
缺点:求得的函数值是近似的.知识点一知识点二知识点三知识点四例4 已知某种型号的摩托车油箱中的剩余油量Q(升)是它行驶时间t(小时)的一次函数.某天老李骑该种摩托车外出旅游,刚开始行驶时,油箱中有油8升,行驶了1小时后,他发现已耗油1.25升.
(1)求油箱中的剩余油量Q(升)与行驶的时间t(小时)的函数解析式,并求出自变量t的取值范围.
(2)在给定的直角坐标系中画出此函数的图象.
(3)从开始行驶算起,如果摩托车以每小时50千米的速度匀速行驶,当油箱中的剩余油量为5.5升时,该摩托车行驶了多少千米?
分析(1)由题意,得Q=-1.25t+8,当Q=0时,t=6.4,得0≤t≤6.4;(2)根据函数的解析式作图;(3)先求出油箱中的剩余油量为5.5升时该摩托车行驶的时间,就可求出路程,路程=速度×时间.知识点一知识点二知识点三知识点四解(1)由题意,得Q=-1.25t+8.
由-1.25t+8=0,得t=6.4.
∴t的取值范围是0≤t≤6.4.
(2)列表:描点、连线,如图所示: 知识点一知识点二知识点三知识点四(3)由5.5=-1.25t+8,得t=2.
∴s=vt=50×2=100.
∴摩托车行驶了100千米.第十九章 一次函数第二讲内容总结:
函数的图象:把自变量与函数的一一对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
函数的表示方法:列表法,图像法,表达式法
作函数的图像:描点、连线
第三讲:正比例函数 研究正比例函数知识点一知识点二知识点三知识点四知识点一正比例函数的由来及定义
列车从哈尔滨出发前往北京,以每小时60千米的速度匀速前进,前进过程中,行驶的时间和路程是什么关系,设行驶时间为X,行驶路程为y,则可以得出
y=60x
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
解读 若某个函数为正比例函数,则可以表示为y=kx(k是常数,k≠0).特别注意,正比例函数中的两个变量的指数都为“1”.
知识点一知识点二知识点三知识点四知识点一知识点二知识点三知识点四知识点一知识点二知识点三知识点四知识点二正比例函数图象的画法
因为两点确定一条直线,所以可用两点法画正比例函数y=kx(k≠0)的图象.一般地,过原点(0,0)和点(1,k)(k是常数,k≠0)的直线,即为正比例函数y=kx(k≠0)的图象.
解读 作正比例函数y=kx(k≠0)的图象时,通常选取(0,0)和(1,k)两点,过这两点作直线即可.但是在实际问题中要注意自变量的取值范围,要灵活选择选取的两点.知识点一知识点二知识点三知识点四例2 在同一直角坐标系中画出下列一次函数的图象:
(1)y=3x;(2)y=5x;(3)y=-5x;(4)y=-3x.
分析根据正比例函数图象的性质可得出它们所经过的两点:原点和(1,k),画图象即可.
解如图所示:
(1)图象过(0,0)和(1,3);
(2)图象过(0,0)和(1,5);
(3)图象过(0,0)和(1,-5);
(4)图象过(0,0)和(1,-3).知识点一知识点二知识点三知识点四知识点一知识点二知识点三知识点四知识点三正比例函数的图象和性质
一般地,正比例函数y=kx(k是常数,k≠0)的图象是一条经过原点的直线,我们称它为直线y=kx.当k>0时,直线y=kx经过第三、第一象限,从左向右上升,即随着x的增大y也增大;当k<0时,直线y=kx经过第二、第四象限,从左向右下降,即随着x的增大y反而减小.
解读 (1)函数的图象“从左向右上升”是指“随着x的增大y也增大”;函数的图象“从左向右下降”是指“随着x的增大y反而减小”.
(2)正比例函数的图象和性质:知识点一知识点二知识点三知识点四例3 下列关于正比例函数y=-5x的说法中,正确的是( )
A.当x=1时,y=5
B.它的图象是一条经过原点的直线
C.y随x的增大而增大
D.它的图象经过第一、三象限
解析A.当x=1时,y=-5,错误;B.正比例函数的图象是一条经过原点的直线,正确;C.根据k<0,得图象经过二、四象限,y随x的增大而减小,错误;D.图象经过第二、四象限,错误.故选B.
答案B知识点一知识点二知识点三知识点四知识点一知识点二知识点三知识点四知识点四确定正比例函数的解析式
确定正比例函数的关系式y=kx(k≠0),实际上就是确定比例系数k(k≠0)的值,一般步骤如下:
(1)先根据条件设出函数解析式为y=kx;
(2)确定一对自变量和函数的对应值(或图象上一个点的坐标);
(3)把对应值代入函数解析式,列出方程,解方程求出k的值;
(4)确定函数解析式.
解读 因为正比例函数的解析式中,只有一个未知字母k,所以只要一个条件就可以确定函数解析式,这个条件可以是图象上一个点的坐标,也可以是一对对应值.知识点一知识点二知识点三知识点四例4 正比例函数如图所示,则这个函数的解析式为( )
A.y=x
B.y=-x
C.y=-2x
解析设这个函数的解析式为y=kx(k≠0),∵函数图象经过(1,-1),
∴-1=k,∴这个函数的解析式为y=-x.故选B.
答案B知识点一知识点二知识点三知识点四拓展点一拓展点二拓展点三拓展点四拓展点五拓展点一根据正比例函数的定义求字母的值
例1 若 是正比例函数,则m的值为( )
A.1 B.-1
解析根据正比例函数的定义,可得2-m2=1,且m-1≠0.∴m=-1.故选B.
答案B拓展点一拓展点二拓展点三拓展点四拓展点五拓展点一拓展点二拓展点三拓展点四拓展点五拓展点三根据正比例函数的性质求字母的取值范围
例3 已知正比例函数y=(k+5)x,且y随x的增大而减小,则k的取值范围是( )
A.k>5 B.k<5
C.k>-5 D.k<-5
解析∵正比例函数y=(k+5)x中若y随x的增大而减小,∴k+5<0.∴k<-5.故选D.
答案D拓展点一拓展点二拓展点三拓展点四拓展点五拓展点一拓展点二拓展点三拓展点四拓展点五拓展点四根据正比例函数的定义和图象求字母的值
例4 正比例函数y=(1-k)x|k-1|的图象经过第二、四象限,那么k的值为( )
A.0 B.-2
C.-1 D.2
解析由题意,得 解得k=2.故选D.
答案D拓展点一拓展点二拓展点三拓展点四拓展点五拓展点一拓展点二拓展点三拓展点四拓展点五拓展点一拓展点二拓展点三拓展点四拓展点五19.2.2 一次函数知识点一知识点二知识点三知识点四知识点五知识点一一次函数的定义
一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数.当b=0时,y=kx+b即为y=kx,所以正比例函数是一种特殊的一次函数.
解读 正比例函数一定是一次函数,是特殊的一次函数,而一次函数包括正比例函数,不一定是正比例函数,只有当b=0时才是正比例函数.知识点一知识点二知识点三知识点四知识点五知识点一知识点二知识点三知识点四知识点五知识点一知识点二知识点三知识点四知识点五知识点二一次函数图象的画法
一次函数y=kx+b(k≠0)图象可以由直线y=kx平移|b|个单位长度得到(当b>0时,向上平移;当b<0时,向下平移).一次函数y=kx+b(k≠0)的图象也是一条直线,我们称为直线y=kx+b.
解读 因为一次函数y=kx+b(k≠0)的图象是一条直线,而两点确定一条直线,这样便可以用两点法来画一次函数的图象.一般地,画正比例函数y=kx(k≠0)的图象,选取(0,0)和(1,k)两点作直线;画一次函数y=kx+b(k≠0)的图象,选取(0,b)和 两点作直线.知识点一知识点二知识点三知识点四知识点五知识点一知识点二知识点三知识点四知识点五分析求出一次函数与x轴、y轴的交点坐标,然后根据两点确定一条直线作出图象即可.
解列表:知识点一知识点二知识点三知识点四知识点五知识点一知识点二知识点三知识点四知识点五知识点一知识点二知识点三知识点四知识点三正比例函数的图象和性质
一般地,正比例函数y=kx(k是常数,k≠0)的图象是一条经过原点的直线,我们称它为直线y=kx.当k>0时,直线y=kx经过第三、第一象限,从左向右上升,即随着x的增大y也增大;当k<0时,直线y=kx经过第二、第四象限,从左向右下降,即随着x的增大y反而减小.
解读 (1)函数的图象“从左向右上升”是指“随着x的增大y也增大”;函数的图象“从左向右下降”是指“随着x的增大y反而减小”.
(2)正比例函数的图象和性质:知识点一知识点二知识点三知识点四知识点五知识点三一次函数的图象和性质
当k>0时,直线y=kx+b从左向右上升;当k<0时,直线y=kx+b从左向右下降.由此可知,一次函数y=kx+b(k,b是常数,k≠0)具有如下性质:
当k>0时,y随x的增大而增大;
当k<0时,y随x的增大而减小.正比例函数的图象和性质:
当k>0时,直线y=kx从左向右上升;当k<0时,直线y=kx从左向右下降.由此可知,一次函数y=kx(k是常数,k≠0)具有如下性质:
当k>0时,y随x的增大而增大;
当k<0时,y随x的增大而减小.
知识点三一次函数的图象和性质
当k>0时,直线y=kx+b从左向右上升;当k<0时,直线y=kx+b从左向右下降.由此可知,一次函数y=kx+b(k,b是常数,k≠0)具有如下性质:
当k>0时,y随x的增大而增大;
当k<0时,y随x的增大而减小.知识点一知识点二知识点三知识点四知识点五例3 已知一次函数y=(2m+1)x+m-3,
(1)若函数图象经过原点,求m的值;
(2)若y随x的增大而增大,求m的取值范围;
(3)一次函数的图象经过第二、三、四象限,求m的取值范围.
分析(1)把点(0,0)代入可求出m的值;(2)根据一次函数的定义及一次函数的增减性列出关于m的不等式,求出m的取值范围;(3)根据题意列出关于m的不等式,求出m的取值范围即可.知识点一知识点二知识点三知识点四知识点五知识点一知识点二知识点三知识点四知识点五
