人教版八年级下数学19.3课题学习 选择方案 :一次函数的应用题课件(40张)
文档属性
| 名称 | 人教版八年级下数学19.3课题学习 选择方案 :一次函数的应用题课件(40张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-06 16:04:27 | ||
图片预览









文档简介
课件40张PPT。一次函数的应用1. 某移动公司对于移动话费推出两种收费方式:
A方案:每月收取基本月租费25元,另收通话费
为0.36元/min;
B方案: 零月租费,通话费为0.5元/min.
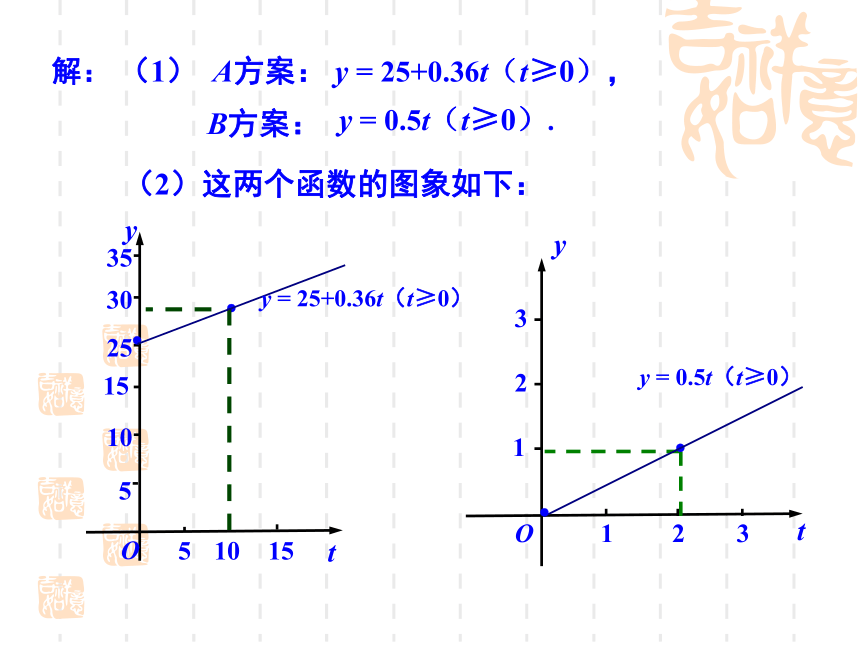
(1)试写出A,B两种方案所付话费y(元)与通话
时间t(min)之间的函数表达式;
(2)分别画出这两个函数的图象;
(3)若林先生每月通话300 min,他选择哪种付费
方式比较合算?(2)这两个函数的图象如下:(3)当t=300时,A方案:
y = 25+0.36t=25+0.36×300=133(元);
B方案:
y = 0.5t=0.5×300=150(元).
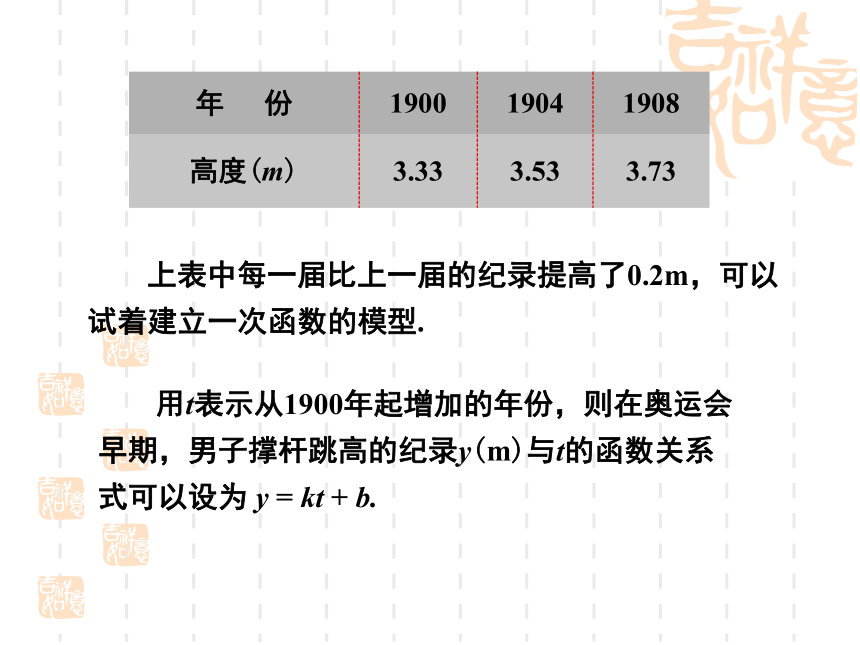
所以此时采用A方案比较合算. 国际奥林匹克运动会早期,男子撑杆跳高的纪录近似值如下表所示: 观察这个表中第二行的数据,可以为奥运会的撑杆跳高纪录与时间的关系建立函数模型吗? 上表中每一届比上一届的纪录提高了0.2m,可以
试着建立一次函数的模型.解得 b = 3.3, k=0.05.公式①就是奥运会早期男子撑杆跳高纪录y与时间t
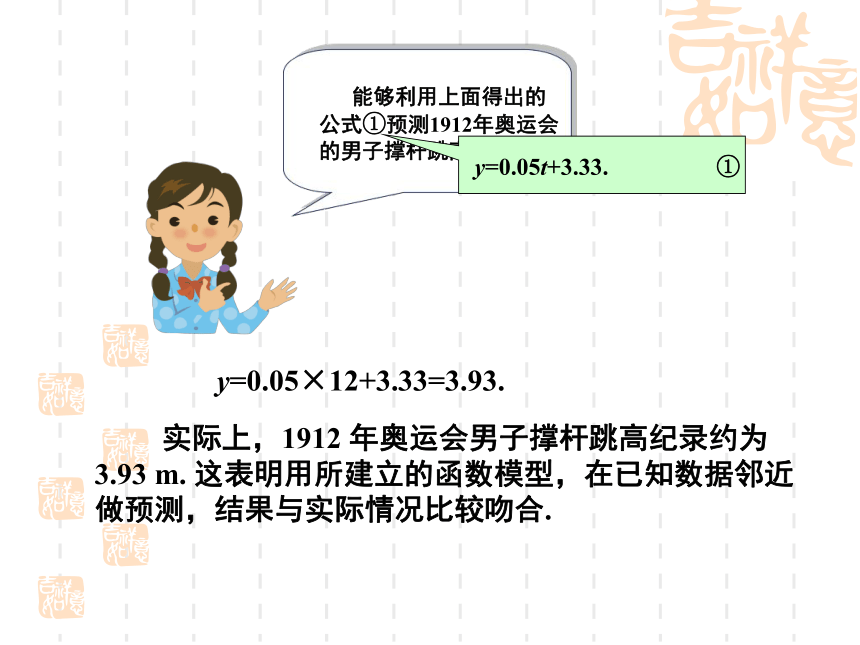
的函数关系式.当t = 8时, y = 3.73,这说明1908年的撑杆跳高
纪录也符合公式①. 实际上,1912 年奥运会男子撑杆跳高纪录约为3.93 m. 这表明用所建立的函数模型,在已知数据邻近做预测,结果与实际情况比较吻合.y=0.05×12+3.33=3.93. 然而,1988年奥运会的男子撑杆跳高纪录是5.90 m,
远低于7.73 m. 这表明用所建立的函数模型远离已知数据
做预测是不可靠的.y=0.05×88+3.33=7.73.请每位同学伸出一只手掌,把大拇指与小拇指尽量张开,两指间的距离称为指距. 已知指距与身高具有如下关系:例2(1) 求身高y与指距x之间的函数表达式;
(2) 当李华的指距为22cm时,你能预测他的身高吗?(1) 求身高y与指距x之间的函数表达式;解得k = 9, b = -20.
于是y = 9x -20. ①将x = 21,y = 169代入①式也符合.
公式①就是身高y与指距x之间的函数表达式.解 当x = 22时, y = 9×22-20 = 178.
因此,李华的身高大约是178 cm.(2) 当李华的指距为22cm时,你能预测他的身高吗? (1)根据表中数据确定该一次函数的表达式;(2)如果蟋蟀1min叫了63次,那么该地当时的气温大约
为多少摄氏度? (3)能用所求出的函数模型来预测蟋蟀在0 ℃时所鸣叫的
次数吗? (1)根据表中数据确定该一次函数的表达式;(2)如果蟋蟀1min叫了63次,那么该地当时的气温大约
为多少摄氏度? (3) 能用所求出的函数模型来预测蟋蟀在0 ℃时所
鸣叫次数吗?答:不能,因为此函数关系是近似的,与实际
生活中的情况有所不符,蟋蟀在0 ℃时可能
不会鸣叫.2. 某商店今年7月初销售纯净水的数量如下表所示:(1)你能为销售纯净水的数量与时间之间的关系
建立函数模型吗?(2)用所求出的函数解析式预测今年7月5日该商店
销售纯净水的数量. 解 销售纯净水的数量y(瓶)与时间t的
函数关系式是
y= 160+(t-1)×5= 5t+155.(1)你能为销售纯净水的数量与时间之间的关系
建立函数模型吗?(2)用所求出的函数解析式预测今年7月5日该商店
销售纯净水的数量.1、小聪和小明沿同一条路同时从学校出发到宁波天一阁查阅资料,学校与天一阁的路程是4千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达天一阁,图中折线O-A-B-C和线段OD分别表示两人离学校的路程(千米)与所经过的时间(分钟)之间的函数关系,请根据图象回答下列问题:
(1)小聪在天一阁查阅资料的时间为__________分钟,小聪返回学校的速度为_______千米/分钟。
(2)请你求出小明离开学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系;
(3)当小聪与小明迎面相遇时,他们离学校的路程是多少千米?【解析】(1)∵30-15=15,4÷15= 4/15 ∴小聪在天一阁查阅资料的时间和小聪返回学校的速度分别是15分钟, 4/15千米/分钟. (2)由图象可知,s是t的正比例函数 设所求函数的解析式为s=kt(k≠0) 代入(45,4),得 4=45k 解得k= 445 ∴s与t的函数关系式s= 445t(0≤t≤45). (3)由图象可知,小聪在30≤t≤45的时段内s是t的一次函数,设函数解析式为s=mt+n(m≠0) 代入(30,4),(45,0),得 {30m+n=445m+n=0 解得 {m=-415n=12 ∴s=- 415t+12(30≤t≤45) 令- 415t+12= 445t,解得t= 1354 当t= 1354时,S= 445× 1354=3 . 答:当小聪与小明迎面相遇时,他们离学校的路程是3千米.2、A,B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即返回.如图是它们离A城的距离y(千米)与行驶时间 x(小时)之间的函数图象. (1)求甲车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围; (2)当它们行驶了7小时时,两车相遇,求乙车速度 【解析】(1)①当0≤x≤6时,y=100x ;
②当6<x≤14时,设y=kx+b,
∵图象过(6,600),(14,0)两点,
∴
∴ y=-75x+1050
∴
∴(2)当x=7时,y=-75×7+1050=525,所以v乙=525÷7=75(千米/小时) 3、甲乙两人同时登西山,甲、乙两人距地面的高度(米)与登山时间(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山的速度是每分钟 米,乙在地提速时距地面的高度为 米.
(2)若乙提速后,乙的速度是甲登山速度的3倍,请分别求出甲、乙二人登山全过程中,登山时距地面的高度(米)与登山时间(分)之间的函数关系式.
(3)登山多长时间时,乙追上了甲?此时乙距地的高度为多少米?【解析】(1)10,30
(2)由图知 ,t=11
∵C(0,100),D(20,300)
∴线段CD的解析式:y甲=10x+100
∵ A(2,30)B(11,300),
折线OAB的解析式为:
(3)由
解得
登山6.5分钟时乙追上甲.
此时乙距地高度为165-30=135(米)(1)若目的地距离学校40km,租用哪家租赁公司的汽车合算?你用什么方法来判断?PQ 学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同,以用车路程 x km计算.甲汽车租赁公司的租费是y1元,乙汽车租赁公司的租费是y2元.(2)目的地距离学校多远时,租用两家租赁公司的汽车所需的费用相同?M(60,150) 学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同,以用车路程 x km计算.甲汽车租赁公司的租费是y1元,乙汽车租赁公司的租费是y2元.(3)若学校租车的预算是200元,那么租用哪家租赁公司的汽车合算?为什么? 学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同,以用车路程 x km计算.甲汽车租赁公司的租费是y1元,乙汽车租赁公司的租费是y2元.(4)如果根据用车路程来选择汽车租赁公司,你能给些建议吗?说说你的理由. 学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同,以用车路程 x km计算.甲汽车租赁公司的租费是y1元,乙汽车租赁公司的租费是y2元.1、如图, lA 、 lB 分别表示A步行与B骑车在同一路上行驶的路程s与时间t的关系.
看图说话(1)B出发时与A相距 km;(2)走了一段路后,自行车发生故障,进行修理,所用的时间是 h;(3)根据图象,你还能说出一条信息吗?1011、如图, lB、lA分别表示A步行与B骑车在同一路上行驶的路程s与时间t的关系.
看图说话(4)若B的自行车不发生故障,保持出发时的速度前进,则出发 h与A相遇,相遇点离A的出发点 km.你能在图中表示出这个相遇点C吗?15C 2、小明和小亮进行了百米赛跑,小丽把他们的竞赛过程用函数图象一一记录下来,若两人在赛跑中距起点的路程s(m)与时间t(s)之间的关系如图所示,根据图象你能叙述他们的跑步过程吗?看图说话1 2、小明和小亮进行了百米赛跑,小丽把他们的竞赛过程用函数图象一一记录下来,若两人在赛跑中距起点的路程s(m)与时间t(s)之间的关系如图所示,根据图象你能叙述他们的跑步过程吗?看图说话 宝应县上网方式有三种:方式一:每月80元包干;方式二:每月上网时间(x)与上网费用(y)的函数关系如图所示;方式三:以0小时为起点,每小时收费1.6元,月收费不超过120元。(1)写出三种方式的函数关系式。(2)小华家每月上网60个小时,选用哪种方式上网合算?一慢车和一快车沿相同路线从A地到B地,所行的路程与时间的函数图象如图所示.试根据图象,回答下列问题:(1)慢车比快车早出发 小时,快车追上慢车时
行驶了 千米,
快车比慢车早
小时
到达B地;(2)求解下列问题:①快车追上慢车需几个小时? ②求慢车、快车的速度.
A方案:每月收取基本月租费25元,另收通话费
为0.36元/min;
B方案: 零月租费,通话费为0.5元/min.
(1)试写出A,B两种方案所付话费y(元)与通话
时间t(min)之间的函数表达式;
(2)分别画出这两个函数的图象;
(3)若林先生每月通话300 min,他选择哪种付费
方式比较合算?(2)这两个函数的图象如下:(3)当t=300时,A方案:
y = 25+0.36t=25+0.36×300=133(元);
B方案:
y = 0.5t=0.5×300=150(元).
所以此时采用A方案比较合算. 国际奥林匹克运动会早期,男子撑杆跳高的纪录近似值如下表所示: 观察这个表中第二行的数据,可以为奥运会的撑杆跳高纪录与时间的关系建立函数模型吗? 上表中每一届比上一届的纪录提高了0.2m,可以
试着建立一次函数的模型.解得 b = 3.3, k=0.05.公式①就是奥运会早期男子撑杆跳高纪录y与时间t
的函数关系式.当t = 8时, y = 3.73,这说明1908年的撑杆跳高
纪录也符合公式①. 实际上,1912 年奥运会男子撑杆跳高纪录约为3.93 m. 这表明用所建立的函数模型,在已知数据邻近做预测,结果与实际情况比较吻合.y=0.05×12+3.33=3.93. 然而,1988年奥运会的男子撑杆跳高纪录是5.90 m,
远低于7.73 m. 这表明用所建立的函数模型远离已知数据
做预测是不可靠的.y=0.05×88+3.33=7.73.请每位同学伸出一只手掌,把大拇指与小拇指尽量张开,两指间的距离称为指距. 已知指距与身高具有如下关系:例2(1) 求身高y与指距x之间的函数表达式;
(2) 当李华的指距为22cm时,你能预测他的身高吗?(1) 求身高y与指距x之间的函数表达式;解得k = 9, b = -20.
于是y = 9x -20. ①将x = 21,y = 169代入①式也符合.
公式①就是身高y与指距x之间的函数表达式.解 当x = 22时, y = 9×22-20 = 178.
因此,李华的身高大约是178 cm.(2) 当李华的指距为22cm时,你能预测他的身高吗? (1)根据表中数据确定该一次函数的表达式;(2)如果蟋蟀1min叫了63次,那么该地当时的气温大约
为多少摄氏度? (3)能用所求出的函数模型来预测蟋蟀在0 ℃时所鸣叫的
次数吗? (1)根据表中数据确定该一次函数的表达式;(2)如果蟋蟀1min叫了63次,那么该地当时的气温大约
为多少摄氏度? (3) 能用所求出的函数模型来预测蟋蟀在0 ℃时所
鸣叫次数吗?答:不能,因为此函数关系是近似的,与实际
生活中的情况有所不符,蟋蟀在0 ℃时可能
不会鸣叫.2. 某商店今年7月初销售纯净水的数量如下表所示:(1)你能为销售纯净水的数量与时间之间的关系
建立函数模型吗?(2)用所求出的函数解析式预测今年7月5日该商店
销售纯净水的数量. 解 销售纯净水的数量y(瓶)与时间t的
函数关系式是
y= 160+(t-1)×5= 5t+155.(1)你能为销售纯净水的数量与时间之间的关系
建立函数模型吗?(2)用所求出的函数解析式预测今年7月5日该商店
销售纯净水的数量.1、小聪和小明沿同一条路同时从学校出发到宁波天一阁查阅资料,学校与天一阁的路程是4千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达天一阁,图中折线O-A-B-C和线段OD分别表示两人离学校的路程(千米)与所经过的时间(分钟)之间的函数关系,请根据图象回答下列问题:
(1)小聪在天一阁查阅资料的时间为__________分钟,小聪返回学校的速度为_______千米/分钟。
(2)请你求出小明离开学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系;
(3)当小聪与小明迎面相遇时,他们离学校的路程是多少千米?【解析】(1)∵30-15=15,4÷15= 4/15 ∴小聪在天一阁查阅资料的时间和小聪返回学校的速度分别是15分钟, 4/15千米/分钟. (2)由图象可知,s是t的正比例函数 设所求函数的解析式为s=kt(k≠0) 代入(45,4),得 4=45k 解得k= 445 ∴s与t的函数关系式s= 445t(0≤t≤45). (3)由图象可知,小聪在30≤t≤45的时段内s是t的一次函数,设函数解析式为s=mt+n(m≠0) 代入(30,4),(45,0),得 {30m+n=445m+n=0 解得 {m=-415n=12 ∴s=- 415t+12(30≤t≤45) 令- 415t+12= 445t,解得t= 1354 当t= 1354时,S= 445× 1354=3 . 答:当小聪与小明迎面相遇时,他们离学校的路程是3千米.2、A,B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即返回.如图是它们离A城的距离y(千米)与行驶时间 x(小时)之间的函数图象. (1)求甲车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围; (2)当它们行驶了7小时时,两车相遇,求乙车速度 【解析】(1)①当0≤x≤6时,y=100x ;
②当6<x≤14时,设y=kx+b,
∵图象过(6,600),(14,0)两点,
∴
∴ y=-75x+1050
∴
∴(2)当x=7时,y=-75×7+1050=525,所以v乙=525÷7=75(千米/小时) 3、甲乙两人同时登西山,甲、乙两人距地面的高度(米)与登山时间(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山的速度是每分钟 米,乙在地提速时距地面的高度为 米.
(2)若乙提速后,乙的速度是甲登山速度的3倍,请分别求出甲、乙二人登山全过程中,登山时距地面的高度(米)与登山时间(分)之间的函数关系式.
(3)登山多长时间时,乙追上了甲?此时乙距地的高度为多少米?【解析】(1)10,30
(2)由图知 ,t=11
∵C(0,100),D(20,300)
∴线段CD的解析式:y甲=10x+100
∵ A(2,30)B(11,300),
折线OAB的解析式为:
(3)由
解得
登山6.5分钟时乙追上甲.
此时乙距地高度为165-30=135(米)(1)若目的地距离学校40km,租用哪家租赁公司的汽车合算?你用什么方法来判断?PQ 学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同,以用车路程 x km计算.甲汽车租赁公司的租费是y1元,乙汽车租赁公司的租费是y2元.(2)目的地距离学校多远时,租用两家租赁公司的汽车所需的费用相同?M(60,150) 学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同,以用车路程 x km计算.甲汽车租赁公司的租费是y1元,乙汽车租赁公司的租费是y2元.(3)若学校租车的预算是200元,那么租用哪家租赁公司的汽车合算?为什么? 学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同,以用车路程 x km计算.甲汽车租赁公司的租费是y1元,乙汽车租赁公司的租费是y2元.(4)如果根据用车路程来选择汽车租赁公司,你能给些建议吗?说说你的理由. 学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同,以用车路程 x km计算.甲汽车租赁公司的租费是y1元,乙汽车租赁公司的租费是y2元.1、如图, lA 、 lB 分别表示A步行与B骑车在同一路上行驶的路程s与时间t的关系.
看图说话(1)B出发时与A相距 km;(2)走了一段路后,自行车发生故障,进行修理,所用的时间是 h;(3)根据图象,你还能说出一条信息吗?1011、如图, lB、lA分别表示A步行与B骑车在同一路上行驶的路程s与时间t的关系.
看图说话(4)若B的自行车不发生故障,保持出发时的速度前进,则出发 h与A相遇,相遇点离A的出发点 km.你能在图中表示出这个相遇点C吗?15C 2、小明和小亮进行了百米赛跑,小丽把他们的竞赛过程用函数图象一一记录下来,若两人在赛跑中距起点的路程s(m)与时间t(s)之间的关系如图所示,根据图象你能叙述他们的跑步过程吗?看图说话1 2、小明和小亮进行了百米赛跑,小丽把他们的竞赛过程用函数图象一一记录下来,若两人在赛跑中距起点的路程s(m)与时间t(s)之间的关系如图所示,根据图象你能叙述他们的跑步过程吗?看图说话 宝应县上网方式有三种:方式一:每月80元包干;方式二:每月上网时间(x)与上网费用(y)的函数关系如图所示;方式三:以0小时为起点,每小时收费1.6元,月收费不超过120元。(1)写出三种方式的函数关系式。(2)小华家每月上网60个小时,选用哪种方式上网合算?一慢车和一快车沿相同路线从A地到B地,所行的路程与时间的函数图象如图所示.试根据图象,回答下列问题:(1)慢车比快车早出发 小时,快车追上慢车时
行驶了 千米,
快车比慢车早
小时
到达B地;(2)求解下列问题:①快车追上慢车需几个小时? ②求慢车、快车的速度.
