人教版数学八年级下19.2.2一次函数课件(17张)
文档属性
| 名称 | 人教版数学八年级下19.2.2一次函数课件(17张) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-05 15:09:18 | ||
图片预览


文档简介
课件17张PPT。一次函数的图象
1、通过画图观察分析一次函数的图象形状特征是什么。
2、归结画一次函数图象的简便方法。
3、如果某些一次函数解析式有相同或相似之处,则它们的图象会有什么特征。探究目标一次函数的图象做一做:
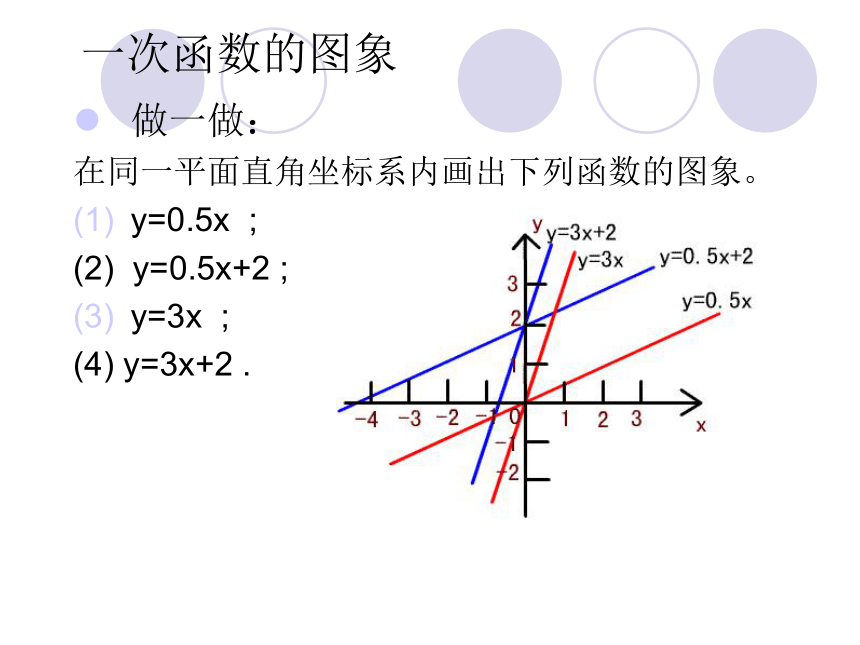
在同一平面直角坐标系内画出下列函数的图象。
y=0.5x ;
(2) y=0.5x+2 ;
y=3x ;
(4) y=3x+2 .
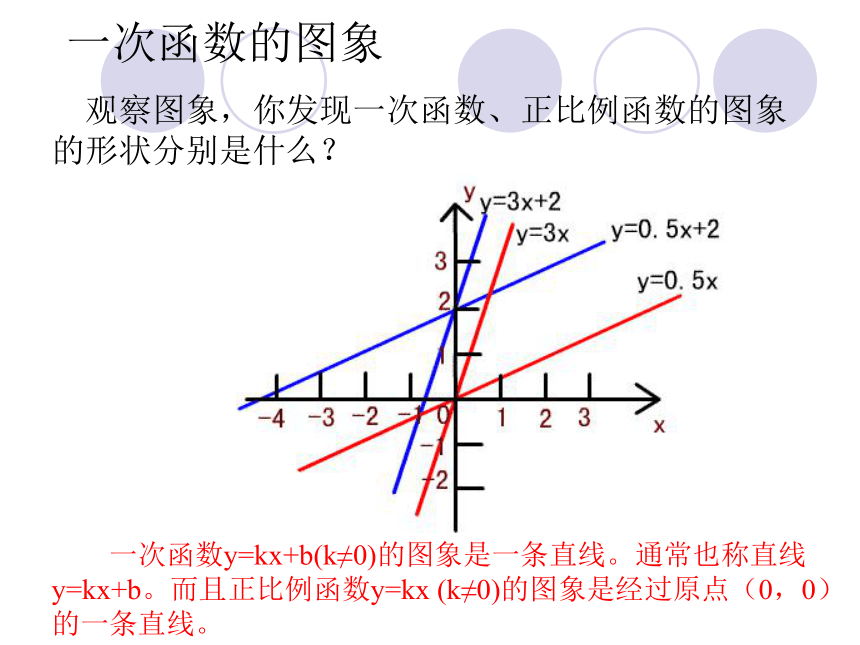
一次函数的图象 观察图象,你发现一次函数、正比例函数的图象的形状分别是什么?
一次函数y=kx+b(k≠0)的图象是一条直线。通常也称直线y=kx+b。而且正比例函数y=kx (k≠0)的图象是经过原点(0,0)的一条直线。一次函数的图象做一做:
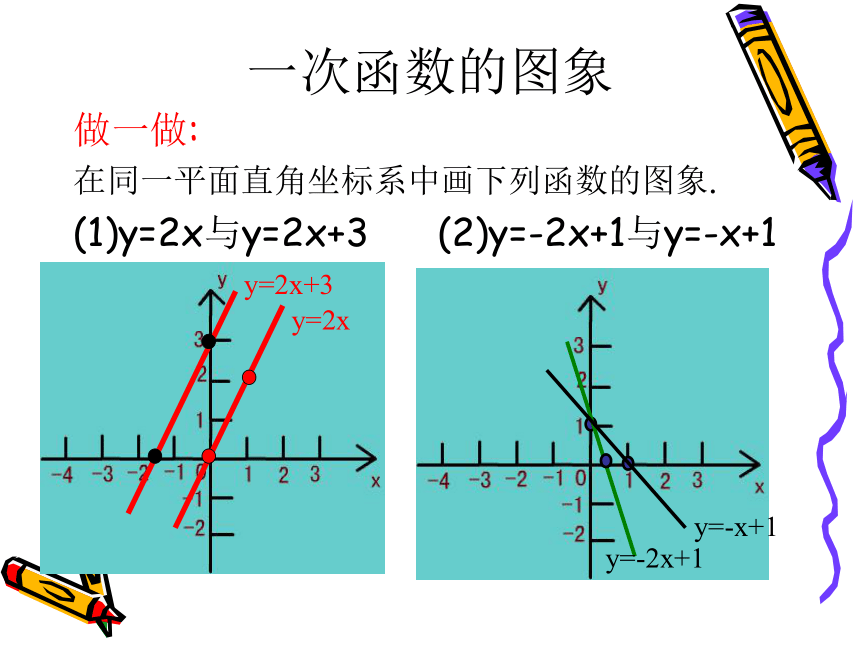
在同一平面直角坐标系中画下列函数的图象.
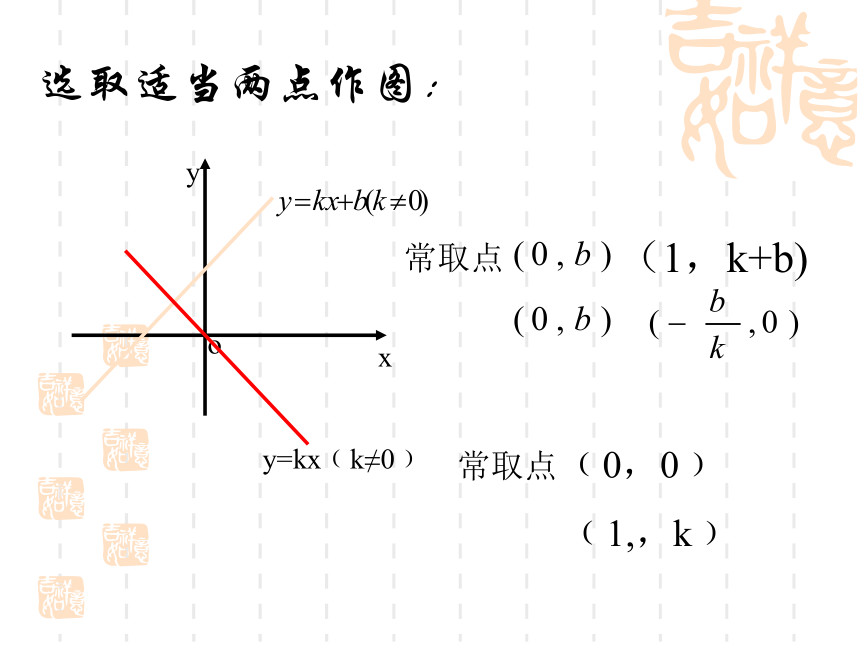
(1)y=2x与y=2x+3 (2)y=-2x+1与y=-x+1y=2xy=2x+3y=-2x+1y=-x+1选取适当两点作图:y=kx﹙k≠0﹚常取点 ﹙0,0﹚
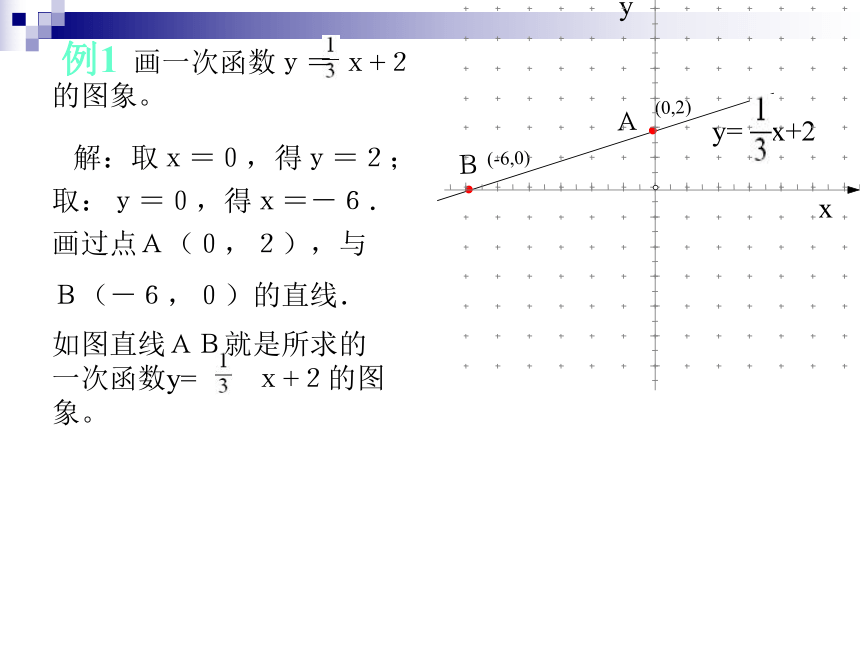
﹙1,,k﹚常取点解:取x=0,得y=2;取:y=0,得x=-6.画过点A(0,2),与
B(-6,0)的直线.x一次函数的图象认真观察上述四个函数的图象的特点,比较下列各对函数的相同点与不同点:
(1) y=3x与y=3x+2 (2) y=0.5x与y=0.5x+2
(3) y=3x+2与y=0.5x+2
观察与思考:一次函数的图象(1) y=3x与y=3x+2 (2) y=0.5x与y=0.5x+2
当k1=k2 , b1≠b2时,两直线平行,可以通过平移其中的一条直线得到另一条直线.一次函数的图象 (3) y=3x+2与y=0.5x+2 当k1=k2 , b1≠b2时,两直线平行,可以通过平移其中的一条直线得到另一条直线.一次函数的图象练一练:
(1)直线y=2x-3可以由直线y=2x经过____________而得到; 直线y=-3x+2可以由直线y=-3x经过_______________而得到;直线y=x+2可以由直线y=x-3经过_________________而得到.
(2)直线y=2x+5与直线y=-3x+5都经过轴上的同一点(___,___).
(3)将直线y=-2x-1向上平移3个单位,得到的直线是______.
y=-2x+2向下平移3个单位向上平移2个单位向下平移5个单位 0 5
探讨一下吧!y=2xy=2x+3y=-2x+1当k>0时,直线从左向右呈 趋势;
当k<0时,直线从左向右呈 趋势;
当b>0时,直线交于y轴 ;
当b<0时,直线交于y轴 ;当b=0时直线过 。
y=-x+1y=x-2上升下降上半轴下半轴原点1、看图象,确定一次函数y=kx+b(k≠0)
中k,b的符号。k<0
b<0k>0
b>0
k<0
b=0数行结合试一试吧看一看、议一议下列函数草图是否正确,如果错误,应如何画?为什么?y=1.5xyx0y=-2x+3yx0y=kx+b﹙k>0,b<0﹚yx0y=-2x+3xy0正确为:xy0正确为:y=kx+b﹙k>0,b<0﹚正确为:y=1.5xxy0一次函数的图象小结:
1、一次函数、正比例函数图象的特征:
一次函数y=kx+b(k≠0)的图象是一条直线。通常也称直线y=kx+b。而且正比例函数y=kx (k≠0)的图象是经过原点(0,0)的一条直线。
当k1=k2 , b1≠b2时,两直线平行,可以通过平移其中的一条直线得到另一条直线. 当k1=k2 , b1≠b2时,两直线平行,可以通过平移其中的一条直线得到另一条直线.
当k>0时,直线从左向右呈上升趋势;
当k<0时,直线从左向右呈下降趋势;
当b>0时,直线交于y轴上半轴;
当b<0时,直线交于y轴下半轴;当b=0时直线过原点。
2、一次函数、正比例图象的画法:
只要在图象上找到两点的坐标,在坐标系中描出这两点,再经过这两点画直线即可。
1、在同一直角坐标系中画出下列函数的图象,并说出它们有什么关系:
(1)y=-2x;
(2)y=-2x-4牛刀小试:
3、已知一次函数y=kx+b(k≠0)中 ①k>0,b<0 ②k<0,b>0,试作图。 2、(1)将直线y=3x向下平移2个单位,得到直线 (2)将直线y=-x-5向上平移5个单位,得到直线
y=-2x;2)y=-2x-4
y=-2x与 y=-2x-4平行。y=3x-2y=-x
1、通过画图观察分析一次函数的图象形状特征是什么。
2、归结画一次函数图象的简便方法。
3、如果某些一次函数解析式有相同或相似之处,则它们的图象会有什么特征。探究目标一次函数的图象做一做:
在同一平面直角坐标系内画出下列函数的图象。
y=0.5x ;
(2) y=0.5x+2 ;
y=3x ;
(4) y=3x+2 .
一次函数的图象 观察图象,你发现一次函数、正比例函数的图象的形状分别是什么?
一次函数y=kx+b(k≠0)的图象是一条直线。通常也称直线y=kx+b。而且正比例函数y=kx (k≠0)的图象是经过原点(0,0)的一条直线。一次函数的图象做一做:
在同一平面直角坐标系中画下列函数的图象.
(1)y=2x与y=2x+3 (2)y=-2x+1与y=-x+1y=2xy=2x+3y=-2x+1y=-x+1选取适当两点作图:y=kx﹙k≠0﹚常取点 ﹙0,0﹚
﹙1,,k﹚常取点解:取x=0,得y=2;取:y=0,得x=-6.画过点A(0,2),与
B(-6,0)的直线.x一次函数的图象认真观察上述四个函数的图象的特点,比较下列各对函数的相同点与不同点:
(1) y=3x与y=3x+2 (2) y=0.5x与y=0.5x+2
(3) y=3x+2与y=0.5x+2
观察与思考:一次函数的图象(1) y=3x与y=3x+2 (2) y=0.5x与y=0.5x+2
当k1=k2 , b1≠b2时,两直线平行,可以通过平移其中的一条直线得到另一条直线.一次函数的图象 (3) y=3x+2与y=0.5x+2 当k1=k2 , b1≠b2时,两直线平行,可以通过平移其中的一条直线得到另一条直线.一次函数的图象练一练:
(1)直线y=2x-3可以由直线y=2x经过____________而得到; 直线y=-3x+2可以由直线y=-3x经过_______________而得到;直线y=x+2可以由直线y=x-3经过_________________而得到.
(2)直线y=2x+5与直线y=-3x+5都经过轴上的同一点(___,___).
(3)将直线y=-2x-1向上平移3个单位,得到的直线是______.
y=-2x+2向下平移3个单位向上平移2个单位向下平移5个单位 0 5
探讨一下吧!y=2xy=2x+3y=-2x+1当k>0时,直线从左向右呈 趋势;
当k<0时,直线从左向右呈 趋势;
当b>0时,直线交于y轴 ;
当b<0时,直线交于y轴 ;当b=0时直线过 。
y=-x+1y=x-2上升下降上半轴下半轴原点1、看图象,确定一次函数y=kx+b(k≠0)
中k,b的符号。k<0
b<0k>0
b>0
k<0
b=0数行结合试一试吧看一看、议一议下列函数草图是否正确,如果错误,应如何画?为什么?y=1.5xyx0y=-2x+3yx0y=kx+b﹙k>0,b<0﹚yx0y=-2x+3xy0正确为:xy0正确为:y=kx+b﹙k>0,b<0﹚正确为:y=1.5xxy0一次函数的图象小结:
1、一次函数、正比例函数图象的特征:
一次函数y=kx+b(k≠0)的图象是一条直线。通常也称直线y=kx+b。而且正比例函数y=kx (k≠0)的图象是经过原点(0,0)的一条直线。
当k1=k2 , b1≠b2时,两直线平行,可以通过平移其中的一条直线得到另一条直线. 当k1=k2 , b1≠b2时,两直线平行,可以通过平移其中的一条直线得到另一条直线.
当k>0时,直线从左向右呈上升趋势;
当k<0时,直线从左向右呈下降趋势;
当b>0时,直线交于y轴上半轴;
当b<0时,直线交于y轴下半轴;当b=0时直线过原点。
2、一次函数、正比例图象的画法:
只要在图象上找到两点的坐标,在坐标系中描出这两点,再经过这两点画直线即可。
1、在同一直角坐标系中画出下列函数的图象,并说出它们有什么关系:
(1)y=-2x;
(2)y=-2x-4牛刀小试:
3、已知一次函数y=kx+b(k≠0)中 ①k>0,b<0 ②k<0,b>0,试作图。 2、(1)将直线y=3x向下平移2个单位,得到直线 (2)将直线y=-x-5向上平移5个单位,得到直线
y=-2x;2)y=-2x-4
y=-2x与 y=-2x-4平行。y=3x-2y=-x
