人教版数学八年级下册19.2.2一次函数的面积问题(专题)课件(31张)
文档属性
| 名称 | 人教版数学八年级下册19.2.2一次函数的面积问题(专题)课件(31张) |  | |
| 格式 | zip | ||
| 文件大小 | 204.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-06 16:12:23 | ||
图片预览



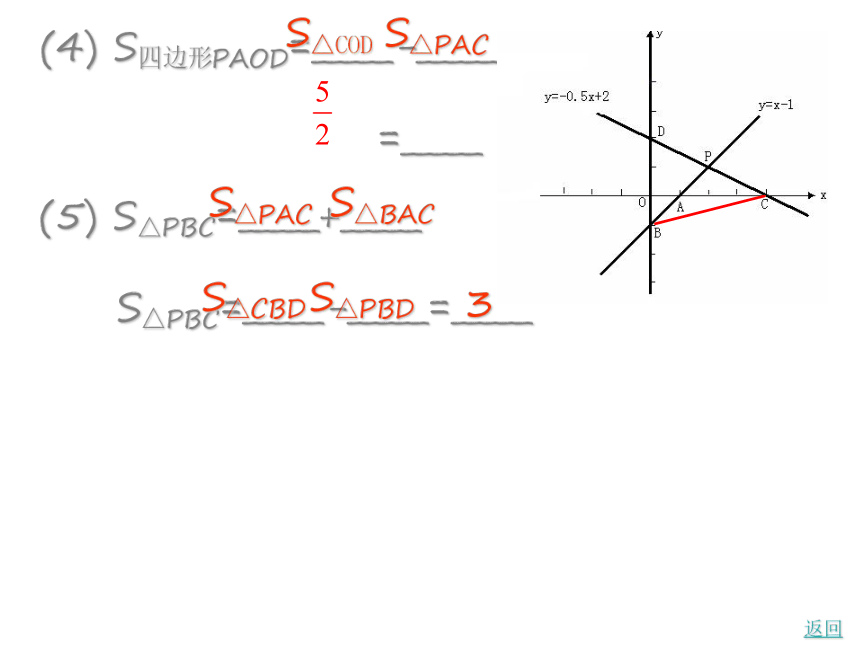

文档简介
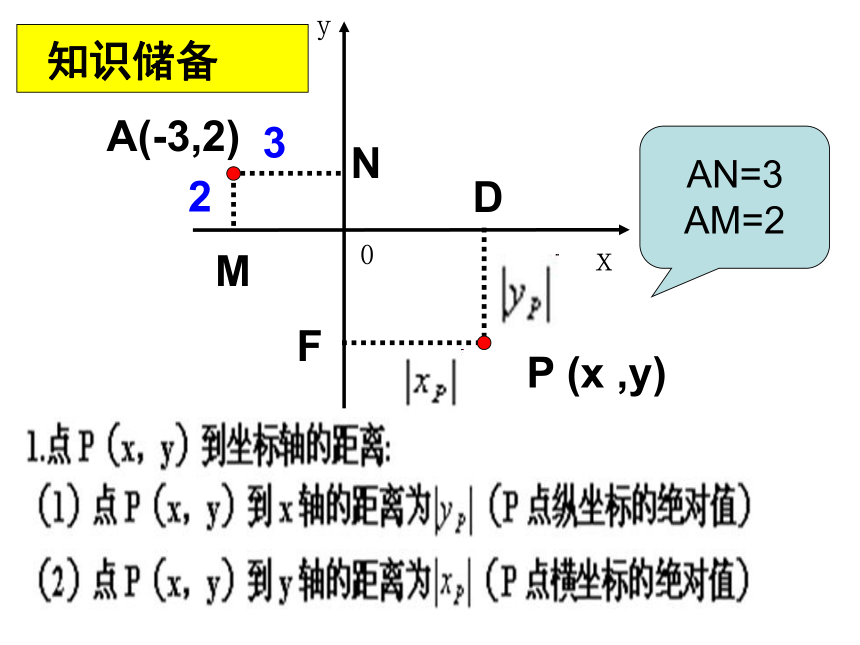
课件31张PPT。与一次函数有关的面积问题专题学习A(-3,2)P (x ,y)知识储备AN=3
AM=21.y=-x+2与x轴的交点坐标是______,与y轴的交点坐标是_____
2.直线y=2x+5与y= x+5的交点坐标______.
3.函数y=3x-2与函数y=2x+1的交点坐标______.课前热身(2,0)(0,2)(0,5)(3,7)1.点A(-1,2)到x轴距离___,到y轴距离____。
任意一点P(x,y)到x轴距离___,到y轴距离____。
2.在x轴上点M(-3,0),点 N(5,0),则MN的长度____。
在x轴上点M(a,0),点 N(b,0),则MN的长度_____
_______。
3.在y轴上点P(0,m),点 Q(0,n),则PQ的长度____
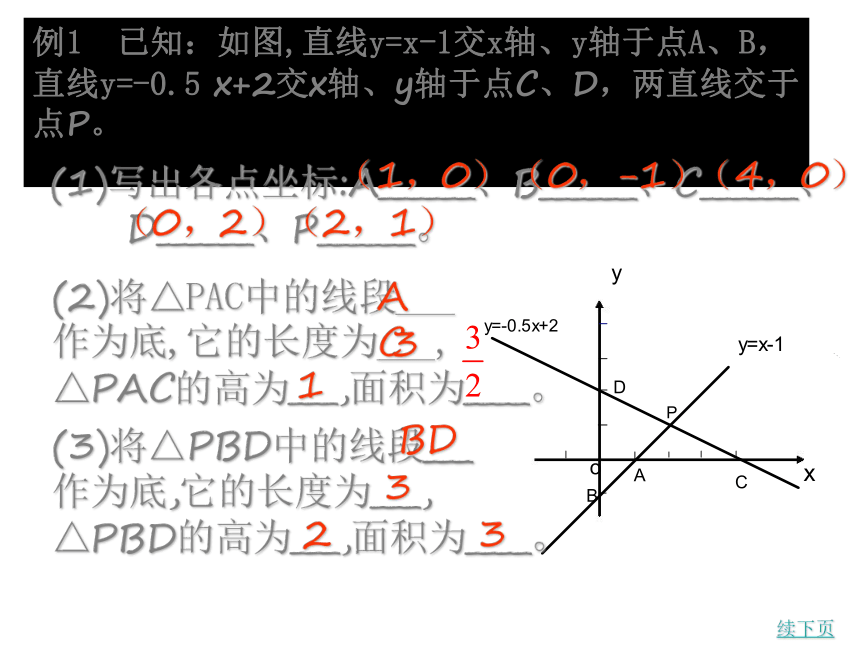
___________.课前热身21|y||x||a-b|或|b-a||m-n|或|n-m|8例1 已知:如图,直线y=x-1交x轴、y轴于点A、B, 直线y=-0.5 x+2交x轴、y轴于点C、D,两直线交于 点P。
续下页(1)写出各点坐标:A______、B______、C______、
D______、P______。(1,0)(0,-1)(4,0)(0,2)(2,1)(2)将△PAC中的线段___
作为底,它的长度为___,
△PAC的高为___,面积为____。
AC31(3)将△PBD中的线段___
作为底,它的长度为___,
△PBD的高为___,面积为____。BD323返回 (4) S四边形PAOD=_____-_____
=_____
S△CODS△PAC(5) S△PBC=_____+_____
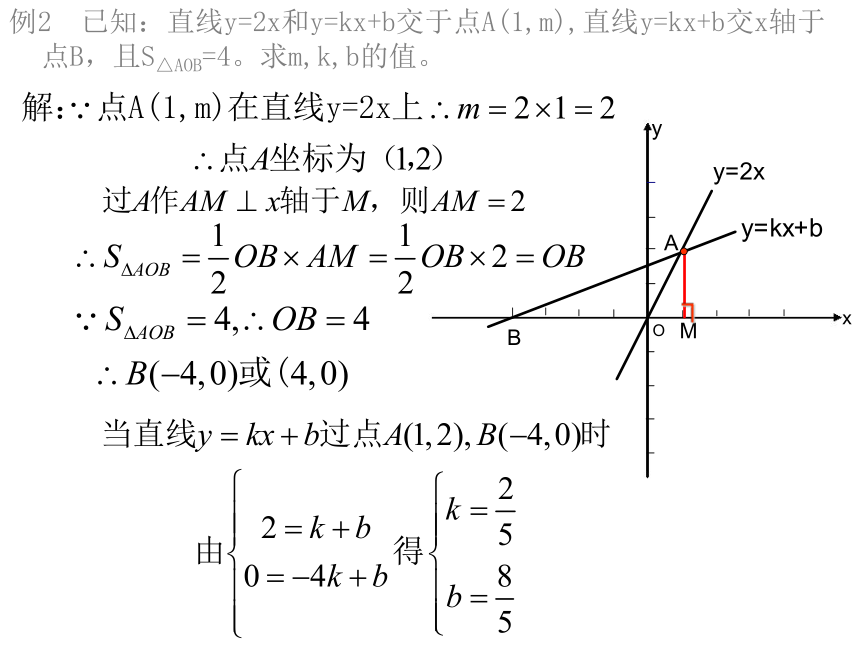
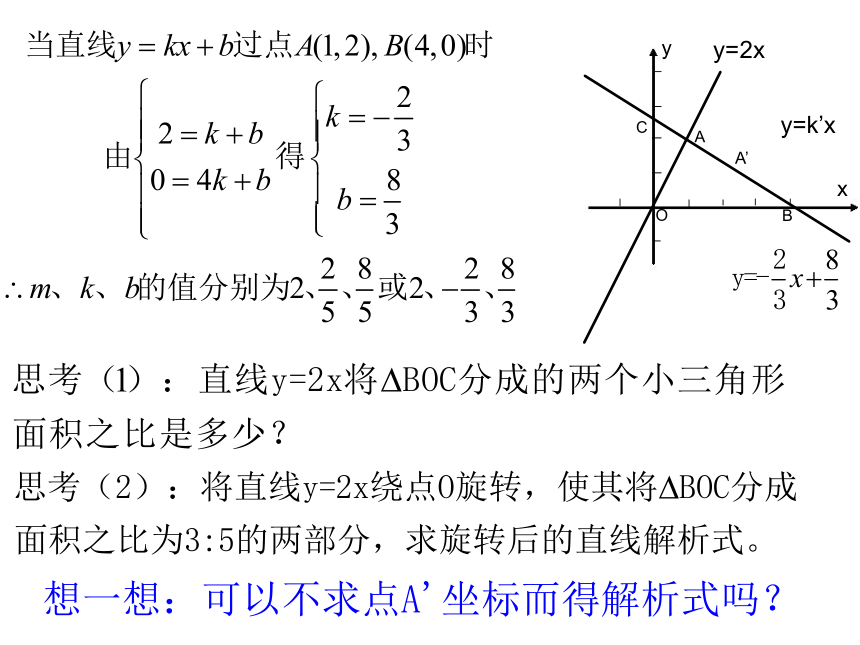
S△PBC=_____-_____=_____S△PACS△BACS△PBDS△CBD3例2 已知:直线y=2x和y=kx+b交于点A(1,m),直线y=kx+b交x轴于点B,且S△AOB=4。求m,k,b的值。
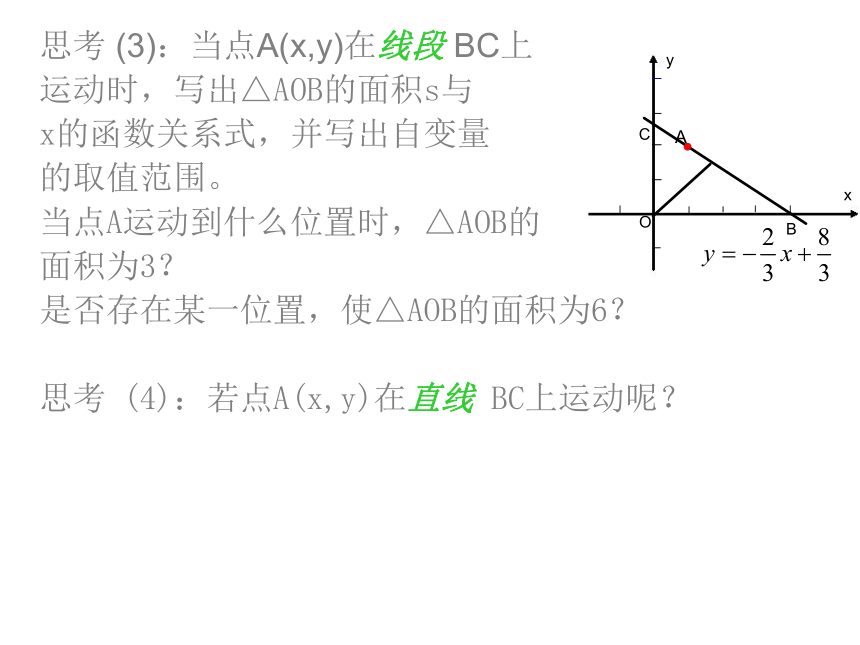
┐思考 (3):当点A(x,y)在线段 BC上
运动时,写出△AOB的面积s与
x的函数关系式,并写出自变量
的取值范围。
当点A运动到什么位置时,△AOB的
面积为3?
是否存在某一位置,使△AOB的面积为6?
思考 (4):若点A(x,y)在直线 BC上运动呢?例1:已知一次函数 .
(1)求图象与 轴交点A, 与 轴交点B的坐标.
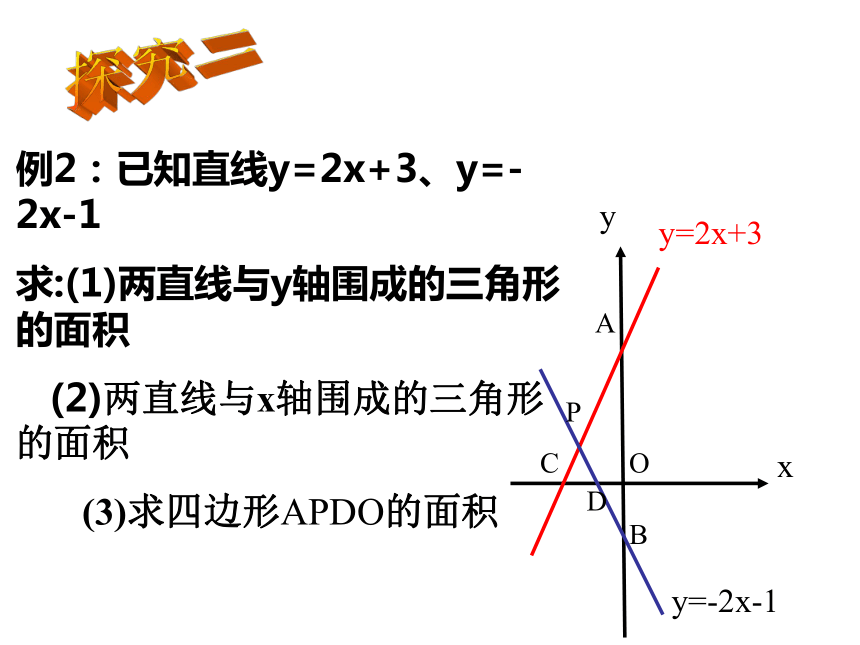
(2)求图象与坐标轴所围成的三角形面积. 探究一例2:已知直线y=2x+3、y=-2x-1
求:(1)两直线与y轴围成的三角形的面积
(2)两直线与x轴围成的三角形的面积
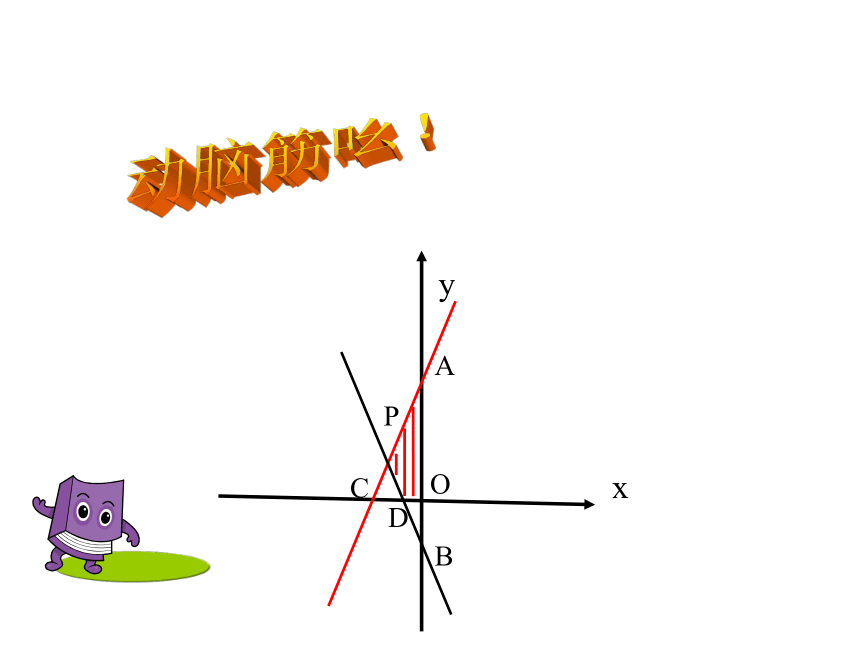
(3)求四边形APDO的面积xyOy=2x+3y=-2x-1ABCDP探究二 xyOABCDP动脑筋吆! xyOABCD(a,b)
P总结:
两直线与y轴围成的面积:AB为底,点P的横坐标的绝对值为高。
|a||b|两直线与x轴围成的面积:CD为底,点P的纵坐标的绝对值为高练习:已知直线y=x+3、y=-x+1
(1)两直线与x轴围成的三角形的面积
(2)两直线与y轴围成的三角形的面积
(3)求四边形AOCP的面积 xyOy=x+3y=-x+1ABCDP你学会了吗?例2:已知直线y=ax+3分别与x轴和y轴交于
A、D两点,直线y=-x+b与x轴和y轴交于点B、C两
点,并且两直线交点P为(2,2)
(1)求两直线解析式;
(2)求四边形AOCP的面积.
xyOy=ax+3y=-x+bABDP变式C例3: 已知:点P是一次函数y=-2x+8的图象上一点,如果图象与x轴交于Q点,且△OPQ的面积等于6,求P点的坐标。xyoy=-2x+8QP探究三P变式、若一次函数的图象交x轴于点A(-6,0),交正比例函数的图象于点B,且点B在第二象限,它的横坐标为- 4,又知:S△AOB=15,求直线AB的解析式。A(-6,0)(-4, ) By例1:已知一次函数 .
(1)求图象与 轴交点A, 与 轴交点B的坐标.
(2)求图象与坐标轴所围成的三角形面积. 探究一比比谁最快牛刀小试求:直线y=2x+4与两坐标轴所围成面积S=42.一次函数 y=kx+b (k,b 为常数,且k≠0)
的图像与x轴、y轴交点坐标.与y轴交点坐标:
B:(0,b)3. 已知:直线 y= 2x+1与直线 y=-x+4相交于点 A,求交点A的坐标.2x+1=-x+4方法1(方程组):方法2(方程):变式训练1: 1.已知直线y=kx+b与x轴交于点(4,0) ,函数图象与坐标轴所围成的三角形的面积是8,求直线的解析式.CBAK>0 或 K<0 已知直线y=2x+4与直线y=-x+1求两直线与x轴所围成的三角形的面积.变式训练 2: 如图,已知: 直线y= - x+2分别交
两坐标轴于A、B两点,M是线段AB上一个动点,设M的横坐标为x,△OMB的面积为S.
(1)写出S与x的函数关系式;
(2)若△OMB的面积为8,求点M的坐标;
若 M在直线AB上能力提升:(4,0)(0,2)看看谁最强如图:直线OC、BC的函数关系式分别为
y=x和y=-2x+6,动点P(x,0)在线段OB上移动挑战自我高手是你吗?1)求点C的坐标;2)若点A(0,1)
当点P运动到什么位置,AP+CP最小;A(0,1)CDP 如图:直线OC、BC的函数关系式分别为
y=x和y=-2x+6,动点P(x,0)在线段OB上移动1)求点C的坐标;
2)若A点坐标为(0,1),当点P运动到 么位置时,AP+CP最小;挑战自我高手是你吗?CP F小结1,点到两坐标轴的距离2,求两直线的交点坐标4,点、图形关于直线对称 转化思想、数形结合思想、分类讨论思想3,一次函数图象性质 一次函数的图象交 轴于点A(-6,0),与 轴交于B,若△AOB的面积为12,且 随 的增大而减少,求一次函数的解析式.自我检测2、直线 与 轴, 轴分别交于点A和点B.另一直线 经过点C(1,0)且把△AOB分成两部分面积相等,求 、 的值.自我检测
AM=21.y=-x+2与x轴的交点坐标是______,与y轴的交点坐标是_____
2.直线y=2x+5与y= x+5的交点坐标______.
3.函数y=3x-2与函数y=2x+1的交点坐标______.课前热身(2,0)(0,2)(0,5)(3,7)1.点A(-1,2)到x轴距离___,到y轴距离____。
任意一点P(x,y)到x轴距离___,到y轴距离____。
2.在x轴上点M(-3,0),点 N(5,0),则MN的长度____。
在x轴上点M(a,0),点 N(b,0),则MN的长度_____
_______。
3.在y轴上点P(0,m),点 Q(0,n),则PQ的长度____
___________.课前热身21|y||x||a-b|或|b-a||m-n|或|n-m|8例1 已知:如图,直线y=x-1交x轴、y轴于点A、B, 直线y=-0.5 x+2交x轴、y轴于点C、D,两直线交于 点P。
续下页(1)写出各点坐标:A______、B______、C______、
D______、P______。(1,0)(0,-1)(4,0)(0,2)(2,1)(2)将△PAC中的线段___
作为底,它的长度为___,
△PAC的高为___,面积为____。
AC31(3)将△PBD中的线段___
作为底,它的长度为___,
△PBD的高为___,面积为____。BD323返回 (4) S四边形PAOD=_____-_____
=_____
S△CODS△PAC(5) S△PBC=_____+_____
S△PBC=_____-_____=_____S△PACS△BACS△PBDS△CBD3例2 已知:直线y=2x和y=kx+b交于点A(1,m),直线y=kx+b交x轴于点B,且S△AOB=4。求m,k,b的值。
┐思考 (3):当点A(x,y)在线段 BC上
运动时,写出△AOB的面积s与
x的函数关系式,并写出自变量
的取值范围。
当点A运动到什么位置时,△AOB的
面积为3?
是否存在某一位置,使△AOB的面积为6?
思考 (4):若点A(x,y)在直线 BC上运动呢?例1:已知一次函数 .
(1)求图象与 轴交点A, 与 轴交点B的坐标.
(2)求图象与坐标轴所围成的三角形面积. 探究一例2:已知直线y=2x+3、y=-2x-1
求:(1)两直线与y轴围成的三角形的面积
(2)两直线与x轴围成的三角形的面积
(3)求四边形APDO的面积xyOy=2x+3y=-2x-1ABCDP探究二 xyOABCDP动脑筋吆! xyOABCD(a,b)
P总结:
两直线与y轴围成的面积:AB为底,点P的横坐标的绝对值为高。
|a||b|两直线与x轴围成的面积:CD为底,点P的纵坐标的绝对值为高练习:已知直线y=x+3、y=-x+1
(1)两直线与x轴围成的三角形的面积
(2)两直线与y轴围成的三角形的面积
(3)求四边形AOCP的面积 xyOy=x+3y=-x+1ABCDP你学会了吗?例2:已知直线y=ax+3分别与x轴和y轴交于
A、D两点,直线y=-x+b与x轴和y轴交于点B、C两
点,并且两直线交点P为(2,2)
(1)求两直线解析式;
(2)求四边形AOCP的面积.
xyOy=ax+3y=-x+bABDP变式C例3: 已知:点P是一次函数y=-2x+8的图象上一点,如果图象与x轴交于Q点,且△OPQ的面积等于6,求P点的坐标。xyoy=-2x+8QP探究三P变式、若一次函数的图象交x轴于点A(-6,0),交正比例函数的图象于点B,且点B在第二象限,它的横坐标为- 4,又知:S△AOB=15,求直线AB的解析式。A(-6,0)(-4, ) By例1:已知一次函数 .
(1)求图象与 轴交点A, 与 轴交点B的坐标.
(2)求图象与坐标轴所围成的三角形面积. 探究一比比谁最快牛刀小试求:直线y=2x+4与两坐标轴所围成面积S=42.一次函数 y=kx+b (k,b 为常数,且k≠0)
的图像与x轴、y轴交点坐标.与y轴交点坐标:
B:(0,b)3. 已知:直线 y= 2x+1与直线 y=-x+4相交于点 A,求交点A的坐标.2x+1=-x+4方法1(方程组):方法2(方程):变式训练1: 1.已知直线y=kx+b与x轴交于点(4,0) ,函数图象与坐标轴所围成的三角形的面积是8,求直线的解析式.CBAK>0 或 K<0 已知直线y=2x+4与直线y=-x+1求两直线与x轴所围成的三角形的面积.变式训练 2: 如图,已知: 直线y= - x+2分别交
两坐标轴于A、B两点,M是线段AB上一个动点,设M的横坐标为x,△OMB的面积为S.
(1)写出S与x的函数关系式;
(2)若△OMB的面积为8,求点M的坐标;
若 M在直线AB上能力提升:(4,0)(0,2)看看谁最强如图:直线OC、BC的函数关系式分别为
y=x和y=-2x+6,动点P(x,0)在线段OB上移动挑战自我高手是你吗?1)求点C的坐标;2)若点A(0,1)
当点P运动到什么位置,AP+CP最小;A(0,1)CDP 如图:直线OC、BC的函数关系式分别为
y=x和y=-2x+6,动点P(x,0)在线段OB上移动1)求点C的坐标;
2)若A点坐标为(0,1),当点P运动到 么位置时,AP+CP最小;挑战自我高手是你吗?CP F小结1,点到两坐标轴的距离2,求两直线的交点坐标4,点、图形关于直线对称 转化思想、数形结合思想、分类讨论思想3,一次函数图象性质 一次函数的图象交 轴于点A(-6,0),与 轴交于B,若△AOB的面积为12,且 随 的增大而减少,求一次函数的解析式.自我检测2、直线 与 轴, 轴分别交于点A和点B.另一直线 经过点C(1,0)且把△AOB分成两部分面积相等,求 、 的值.自我检测
