鲁教版(五四制)七年级数学上册1.5 利用三角形全等测距离课件(共26张PPT)
文档属性
| 名称 | 鲁教版(五四制)七年级数学上册1.5 利用三角形全等测距离课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-06 16:20:39 | ||
图片预览




文档简介
(共26张PPT)
利用三角形全等
测距离
1. 通过用三角形全等解决测距离的实际问题,经历
分析问题和解决问题的过程,发展数学建模的素养.
2. 了解数学建模的一般步骤.
3. 能够比较准确的用文字语言、图形语言和符号语言
描述数学对象和表达个人观点.
学习目标
复习引入
全等三角形
的性质
边相等, 角相等
对应
对应
对应边上的 、 分别相等;对应角的 相等,
中线
高线
角平分线
相等, 相等
面积
周长
全等三角形
的判定
全等三角形
的应用
SSS、SAS、ASA、AAS
利用全等三角形解决实际问题的一般步骤是什么呢?
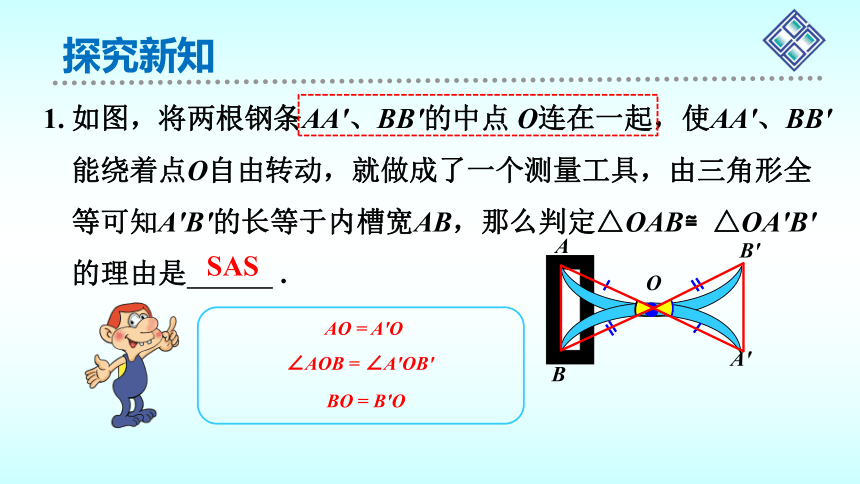
1. 如图,将两根钢条AA′、BB′的中点 O连在一起,使AA′、BB′
能绕着点O自由转动,就做成了一个测量工具,由三角形全
等可知A′B′的长等于内槽宽AB,那么判定△OAB≌△OA′B′
的理由是 .
SAS
探究新知
AO = A′O
∠AOB = ∠A′OB′
BO = B′O
A
B
O
B′
A′
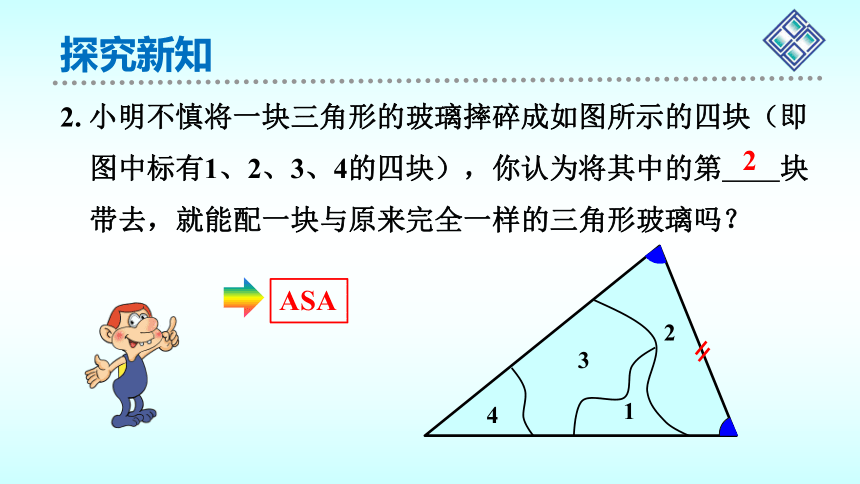
2. 小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即
图中标有1、2、3、4的四块),你认为将其中的第 块
带去,就能配一块与原来完全一样的三角形玻璃吗?
2
ASA
探究新知
2
3
1
4
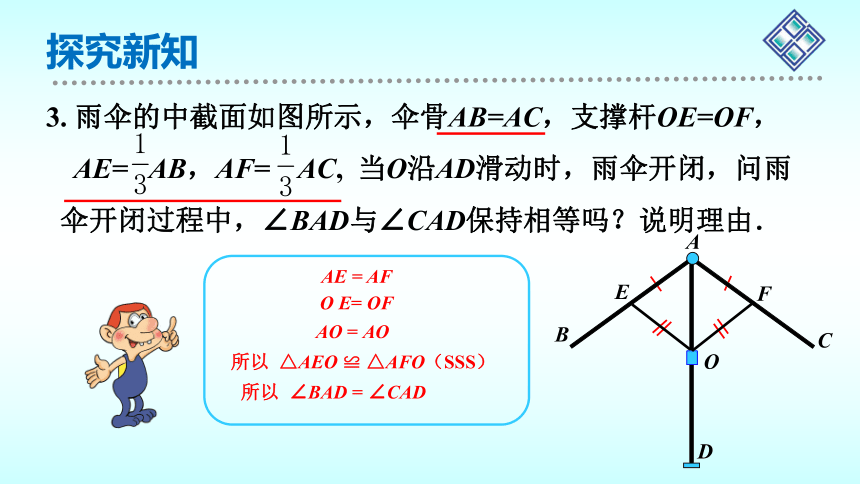
3. 雨伞的中截面如图所示,伞骨AB=AC,支撑杆OE=OF,
AE= AB,AF= AC, 当O沿AD滑动时,雨伞开闭,问雨
伞开闭过程中,∠BAD与∠CAD保持相等吗?说明理由.
探究新知
AE = AF
AO = AO
O E= OF
所以 △AEO ≌ △AFO(SSS)
所以 ∠BAD = ∠CAD
A
E
F
O
B
C
D
探究新知
审题
图形
文字
相等的边、相等的角
在一次战役中,我军阵地与敌军碉堡隔河相望.为了炸掉这个碉堡,需要知道碉堡与我军阵地的距离.在不能过河测量又没有任何测量工具的情况下,一个战士想出了一个办法,为成功炸毁碉堡立了一功.
智慧炸碉堡的故事
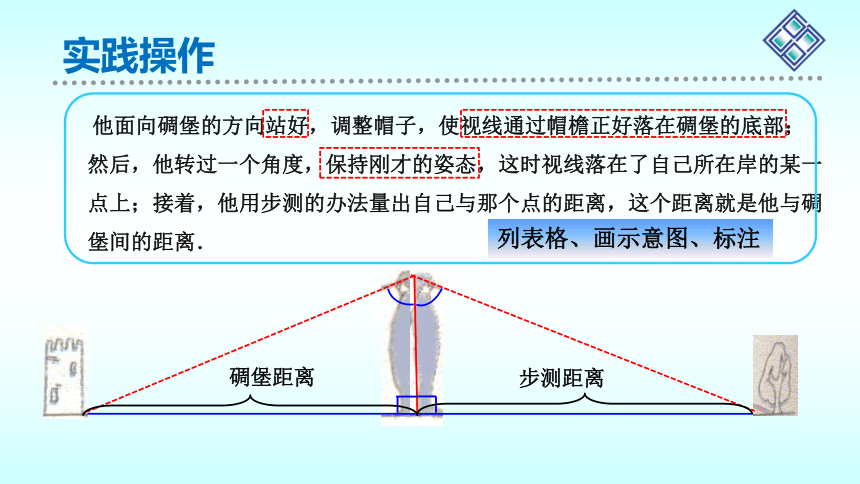
实践操作
他面向碉堡的方向站好,调整帽子,使视线通过帽檐正好落在碉堡的底部; 然后,他转过一个角度,保持刚才的姿态,这时视线落在了自己所在岸的某一点上;接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡间的距离.
步测距离
碉堡距离
实践操作
列表格、画示意图、标注
实践操作
分析两三角形中存在的边角关系,填写下表并在示意图中进行标注.
已 知 问题
边
角
直角( ∠ACB=∠ACD );∠BAC=∠DAC
身高(AC=AC)
A
B
C
D
说明:BC=DC
如图,已知△ABC与△ADC中,∠BAC= ∠DAC,∠ACB= 90 , ∠ACD= 90°,请说明 BC=DC.
实践操作
A
D
C
B
因为
在△ABC与△ADC中
AC = AC
∠BAC = ∠DAC
∠ACB =∠ACD
所以 △ABC ≌ △ADC(ASA)
所以 BC = DC
因为∠ACB = 90°, ∠ACD = 90°
所以 ∠ACB =∠ACD
问题
实践操作
1.不能直接解决的数学问题需要借助 的数学思想解决.
2.本题的解决过程体现了数学建模意识.先发现问题,然后分析抽象出其中的数学元素,借助______________________ 等方法利于更好的理解和分析问题.
画图、标注和列表格
转化
归纳
泰勒斯,公元前7至6世纪的古希腊时期的思想家、科学家、哲学家,希腊最早的哲学学派——米利都学派(也称爱奥尼亚学派)的创始人. 西方思想史上第一位有记载有名字留下来的思想家,被称为“科学和哲学之祖”.泰勒斯曾利用日影来测量金字塔的高度,利用全等三角形和相似三角形的知识用不同的方法测量出轮船与海岸的距离.并准确地预测了公元前585年发生的日食.
古人实践
仰望星空的人---几何鼻祖泰勒斯
如图,泰勒斯在高丘上利用一种简单的工具进行测量.竿EF垂直于地面,在其上有一固定钉子A,另一横杆可以绕A 转动,但可以固定在任一位置上.将该细竿调准到河对岸B的位置,然后转动EF(保持与底面垂直),将细竿对准岸上的某一点C,则根据角边角(ASA)定理,DC = DB.
古人实践
泰勒斯的测量方法
拿破仑军队在行军途中为一河流所阻,一名随军工程师运用泰勒斯的方法迅速测得河流的宽度,因而受到拿破仑的嘉奖.因此,从古希腊开始,角边角定理在测量中一直扮演着重要角色.
古人实践
小明家的附近有一个平坦的大广场,广场中央有一个椭圆形的景观大鱼池.小明在广场上玩时想用绳子测量这个池塘的长,即图中线段AB 的长度,但是绳子不够长,他该怎么办呢?
A
B
探索操作
戴一顶太阳帽,在点B立正站好,自己调整帽子,使视线通过帽檐正好落在池塘对面的点A ,然后转过一个角度,保持刚才的姿势,帽檐不动,这时再望出去,仍让视线通过帽檐,视线所落的位置为点C,测出BC的长,就是A,B间的距离.
在△ADB和△CDB中
所以 △ADB≌△CDB(ASA)
所以 AB = BC
BD = BD
∠DBA =∠DBC
方案一
A
B
D
C
∠ADB = ∠CDB
因为
探索操作
垂直全等法
如图, 戴一顶太阳帽,在点B立正站好,自己调整帽子,使视线通过帽檐正好落在池塘对面的点A,保持姿势和帽檐不动,仍让视线通过帽檐,慢慢往后移动,当视线落到点B时停止,此时所站的位置
为C,测量BC的长度即为A,B间的距离.
方案二
A
B
C
D
E
探索操作
平移全等法
方案三
A
B
(1)先在地上取一个可以直接到达A点、B点的点C;
C
D
E
可操作性
构造全等常用方法
(4)连接DE并测量出它的长度,DE的长度就是A、B间的距离.
(2)连接AC并延长到D,使CD=AC;
(3)连接BC并延长到E,使CE=BC;
探索操作
在△ABC和△DEC中
因为AC=CD,∠ACB=∠DCE,BC=EC
所以 △ABC≌△DEC(SAS)
所以 AB=DE
延长全等法
七下第五章
八下第三章
探索操作
模型
A
B
D
C
A
B
D
E
轴对称
平移
旋转
A
B
C
D
E
探索操作
归纳:
3.数学思想:
不可测距离
构造全等三角形
可测距离
2.方法:
1.知识:
转化思想
平移法构造全等三角形
垂直法构造全等三角形
延长法构造全等三角形
1. 小明站在路中央,先往左看了看,又往右看了看,然后说知道纪念碑相当于5层楼
那么高,你知道他是怎么做到的吗?
发散拓展
A
B
C
D
O
他是怎么做到的呢?
2. 某城市搞亮化工程,如图,在甲楼底部、乙楼顶部分别安装一盏射灯.已知A灯恰好照到
B灯,B灯恰好照到甲楼的顶部,如果两盏灯的光线与水平线的夹角是相等的,那么能否
说甲楼的高度是乙楼的2倍?说说你的看法.
2
1
甲
A
发散拓展
B
甲楼
乙楼
在△ABD和△CBD中
因为∠CBD=∠ABD,BD=BD, ∠CDB=∠ADB
所以 △ABD≌△CBD(ASA)
所以 AD=CD , 所以 AC=2AD
因为 AD=BE , 所以 AC=2BE
A
D
C
B
E
发散拓展
3. 为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P,使点P到楼底距离PB与旗杆高
度相等,等于8米.测得旗杆顶C视线PC与地面夹角 ∠DPC=38°,测楼顶A视线PA与地
面夹角∠APB=52°,量得旗杆与楼之间距离DB=33米,楼高AB= 米.
8米
8米
38°
52°
52°
25米
25
直接条件
文字语言
BP=CD=8米
DB=33米
∠DPC=38°
∠APB=52°
间接条件
PD=25米∠DCP=52°
提取信息
因为∠PCD =∠APB
CD = PB
∠CDP = ∠PBA
所以△CDP ≌ △PBA(ASA)
所以 AB=PD=25米
解答问题
图形语言
符号语言
33米
1. 如图,要量湖两岸相对两点A、B的距离,可以在AB的垂线BF上取两点C、D,使
CD=BC,再作出BF的垂线DE,使A、C、E在一条直线上,这时可得△ABC≌△EDC,
用于判定全等的是( )A.SSS B.SAS C.ASA D.AAS
2. 在一座楼相邻两面墙(两墙面互相垂直),墙根的外面有两点
A,B ,如图所示,请设计方案测量A,B两点间的距离,画出
设计图形,写出设计方案,并说明理由.
课堂练习
A
B
第1题图
C
A
B
D
C
E
参考设计图:
(设计方案和说明略)
(请按暂停键,用时5分钟)
审题
相等的边;相等的角
数量关系;等量关系
类比
建模
解答
探索操作
几何模型
代数模型
类比
选择模型
严谨规范
归纳:
建立数学模型解决问题的一般步骤:
利用三角形全等
测距离
1. 通过用三角形全等解决测距离的实际问题,经历
分析问题和解决问题的过程,发展数学建模的素养.
2. 了解数学建模的一般步骤.
3. 能够比较准确的用文字语言、图形语言和符号语言
描述数学对象和表达个人观点.
学习目标
复习引入
全等三角形
的性质
边相等, 角相等
对应
对应
对应边上的 、 分别相等;对应角的 相等,
中线
高线
角平分线
相等, 相等
面积
周长
全等三角形
的判定
全等三角形
的应用
SSS、SAS、ASA、AAS
利用全等三角形解决实际问题的一般步骤是什么呢?
1. 如图,将两根钢条AA′、BB′的中点 O连在一起,使AA′、BB′
能绕着点O自由转动,就做成了一个测量工具,由三角形全
等可知A′B′的长等于内槽宽AB,那么判定△OAB≌△OA′B′
的理由是 .
SAS
探究新知
AO = A′O
∠AOB = ∠A′OB′
BO = B′O
A
B
O
B′
A′
2. 小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即
图中标有1、2、3、4的四块),你认为将其中的第 块
带去,就能配一块与原来完全一样的三角形玻璃吗?
2
ASA
探究新知
2
3
1
4
3. 雨伞的中截面如图所示,伞骨AB=AC,支撑杆OE=OF,
AE= AB,AF= AC, 当O沿AD滑动时,雨伞开闭,问雨
伞开闭过程中,∠BAD与∠CAD保持相等吗?说明理由.
探究新知
AE = AF
AO = AO
O E= OF
所以 △AEO ≌ △AFO(SSS)
所以 ∠BAD = ∠CAD
A
E
F
O
B
C
D
探究新知
审题
图形
文字
相等的边、相等的角
在一次战役中,我军阵地与敌军碉堡隔河相望.为了炸掉这个碉堡,需要知道碉堡与我军阵地的距离.在不能过河测量又没有任何测量工具的情况下,一个战士想出了一个办法,为成功炸毁碉堡立了一功.
智慧炸碉堡的故事
实践操作
他面向碉堡的方向站好,调整帽子,使视线通过帽檐正好落在碉堡的底部; 然后,他转过一个角度,保持刚才的姿态,这时视线落在了自己所在岸的某一点上;接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡间的距离.
步测距离
碉堡距离
实践操作
列表格、画示意图、标注
实践操作
分析两三角形中存在的边角关系,填写下表并在示意图中进行标注.
已 知 问题
边
角
直角( ∠ACB=∠ACD );∠BAC=∠DAC
身高(AC=AC)
A
B
C
D
说明:BC=DC
如图,已知△ABC与△ADC中,∠BAC= ∠DAC,∠ACB= 90 , ∠ACD= 90°,请说明 BC=DC.
实践操作
A
D
C
B
因为
在△ABC与△ADC中
AC = AC
∠BAC = ∠DAC
∠ACB =∠ACD
所以 △ABC ≌ △ADC(ASA)
所以 BC = DC
因为∠ACB = 90°, ∠ACD = 90°
所以 ∠ACB =∠ACD
问题
实践操作
1.不能直接解决的数学问题需要借助 的数学思想解决.
2.本题的解决过程体现了数学建模意识.先发现问题,然后分析抽象出其中的数学元素,借助______________________ 等方法利于更好的理解和分析问题.
画图、标注和列表格
转化
归纳
泰勒斯,公元前7至6世纪的古希腊时期的思想家、科学家、哲学家,希腊最早的哲学学派——米利都学派(也称爱奥尼亚学派)的创始人. 西方思想史上第一位有记载有名字留下来的思想家,被称为“科学和哲学之祖”.泰勒斯曾利用日影来测量金字塔的高度,利用全等三角形和相似三角形的知识用不同的方法测量出轮船与海岸的距离.并准确地预测了公元前585年发生的日食.
古人实践
仰望星空的人---几何鼻祖泰勒斯
如图,泰勒斯在高丘上利用一种简单的工具进行测量.竿EF垂直于地面,在其上有一固定钉子A,另一横杆可以绕A 转动,但可以固定在任一位置上.将该细竿调准到河对岸B的位置,然后转动EF(保持与底面垂直),将细竿对准岸上的某一点C,则根据角边角(ASA)定理,DC = DB.
古人实践
泰勒斯的测量方法
拿破仑军队在行军途中为一河流所阻,一名随军工程师运用泰勒斯的方法迅速测得河流的宽度,因而受到拿破仑的嘉奖.因此,从古希腊开始,角边角定理在测量中一直扮演着重要角色.
古人实践
小明家的附近有一个平坦的大广场,广场中央有一个椭圆形的景观大鱼池.小明在广场上玩时想用绳子测量这个池塘的长,即图中线段AB 的长度,但是绳子不够长,他该怎么办呢?
A
B
探索操作
戴一顶太阳帽,在点B立正站好,自己调整帽子,使视线通过帽檐正好落在池塘对面的点A ,然后转过一个角度,保持刚才的姿势,帽檐不动,这时再望出去,仍让视线通过帽檐,视线所落的位置为点C,测出BC的长,就是A,B间的距离.
在△ADB和△CDB中
所以 △ADB≌△CDB(ASA)
所以 AB = BC
BD = BD
∠DBA =∠DBC
方案一
A
B
D
C
∠ADB = ∠CDB
因为
探索操作
垂直全等法
如图, 戴一顶太阳帽,在点B立正站好,自己调整帽子,使视线通过帽檐正好落在池塘对面的点A,保持姿势和帽檐不动,仍让视线通过帽檐,慢慢往后移动,当视线落到点B时停止,此时所站的位置
为C,测量BC的长度即为A,B间的距离.
方案二
A
B
C
D
E
探索操作
平移全等法
方案三
A
B
(1)先在地上取一个可以直接到达A点、B点的点C;
C
D
E
可操作性
构造全等常用方法
(4)连接DE并测量出它的长度,DE的长度就是A、B间的距离.
(2)连接AC并延长到D,使CD=AC;
(3)连接BC并延长到E,使CE=BC;
探索操作
在△ABC和△DEC中
因为AC=CD,∠ACB=∠DCE,BC=EC
所以 △ABC≌△DEC(SAS)
所以 AB=DE
延长全等法
七下第五章
八下第三章
探索操作
模型
A
B
D
C
A
B
D
E
轴对称
平移
旋转
A
B
C
D
E
探索操作
归纳:
3.数学思想:
不可测距离
构造全等三角形
可测距离
2.方法:
1.知识:
转化思想
平移法构造全等三角形
垂直法构造全等三角形
延长法构造全等三角形
1. 小明站在路中央,先往左看了看,又往右看了看,然后说知道纪念碑相当于5层楼
那么高,你知道他是怎么做到的吗?
发散拓展
A
B
C
D
O
他是怎么做到的呢?
2. 某城市搞亮化工程,如图,在甲楼底部、乙楼顶部分别安装一盏射灯.已知A灯恰好照到
B灯,B灯恰好照到甲楼的顶部,如果两盏灯的光线与水平线的夹角是相等的,那么能否
说甲楼的高度是乙楼的2倍?说说你的看法.
2
1
甲
A
发散拓展
B
甲楼
乙楼
在△ABD和△CBD中
因为∠CBD=∠ABD,BD=BD, ∠CDB=∠ADB
所以 △ABD≌△CBD(ASA)
所以 AD=CD , 所以 AC=2AD
因为 AD=BE , 所以 AC=2BE
A
D
C
B
E
发散拓展
3. 为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P,使点P到楼底距离PB与旗杆高
度相等,等于8米.测得旗杆顶C视线PC与地面夹角 ∠DPC=38°,测楼顶A视线PA与地
面夹角∠APB=52°,量得旗杆与楼之间距离DB=33米,楼高AB= 米.
8米
8米
38°
52°
52°
25米
25
直接条件
文字语言
BP=CD=8米
DB=33米
∠DPC=38°
∠APB=52°
间接条件
PD=25米∠DCP=52°
提取信息
因为∠PCD =∠APB
CD = PB
∠CDP = ∠PBA
所以△CDP ≌ △PBA(ASA)
所以 AB=PD=25米
解答问题
图形语言
符号语言
33米
1. 如图,要量湖两岸相对两点A、B的距离,可以在AB的垂线BF上取两点C、D,使
CD=BC,再作出BF的垂线DE,使A、C、E在一条直线上,这时可得△ABC≌△EDC,
用于判定全等的是( )A.SSS B.SAS C.ASA D.AAS
2. 在一座楼相邻两面墙(两墙面互相垂直),墙根的外面有两点
A,B ,如图所示,请设计方案测量A,B两点间的距离,画出
设计图形,写出设计方案,并说明理由.
课堂练习
A
B
第1题图
C
A
B
D
C
E
参考设计图:
(设计方案和说明略)
(请按暂停键,用时5分钟)
审题
相等的边;相等的角
数量关系;等量关系
类比
建模
解答
探索操作
几何模型
代数模型
类比
选择模型
严谨规范
归纳:
建立数学模型解决问题的一般步骤:
