人教版七年级数学下册课件:7.1.2平面直角坐标系中求面积(共22张PPT)
文档属性
| 名称 | 人教版七年级数学下册课件:7.1.2平面直角坐标系中求面积(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 571.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-06 16:54:00 | ||
图片预览



文档简介
(共22张PPT)
平面直角坐标系中求面积
几种常见面积问题的求法
一、自主学习
1、(1)已知点P在x轴上,且到y轴的距离为2,
则 点P的坐标为__________
(2)已知点P到x轴的距离为3,到y轴的距离为4,则点P的坐标为_________________________
(3)若A(-1,0),B(4,0),则线段AB的长为____
(4)若A(0,5),B(0,3),则线段AB的长为_____
(5)若A(-3,-2),B(-5,-2),则线段AB的长为_____
(6)若A(3,2),B(3,-3),则线段AB的长为___
(-2,0)(2,0)
(4,3)(-4,3)(4,-3)(-4,-3)
5
2
2
5
题型一
底边在坐标轴上三角形面积的求法
*
*
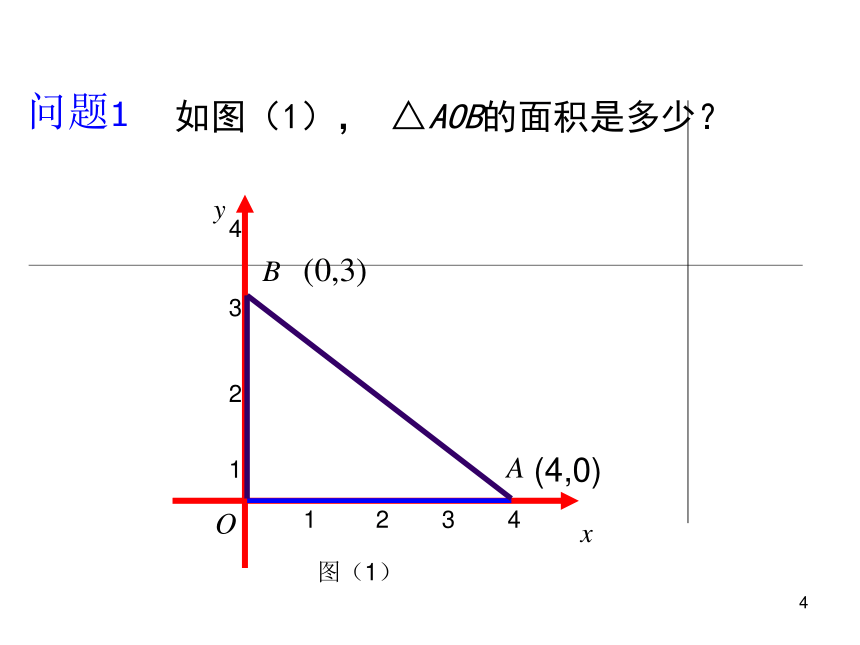
如图(1), △AOB的面积是多少?
问题1
y
O
x
图(1)
A
B
4
3
2
1
1 2 3 4
(4,0)
(0,3)
*
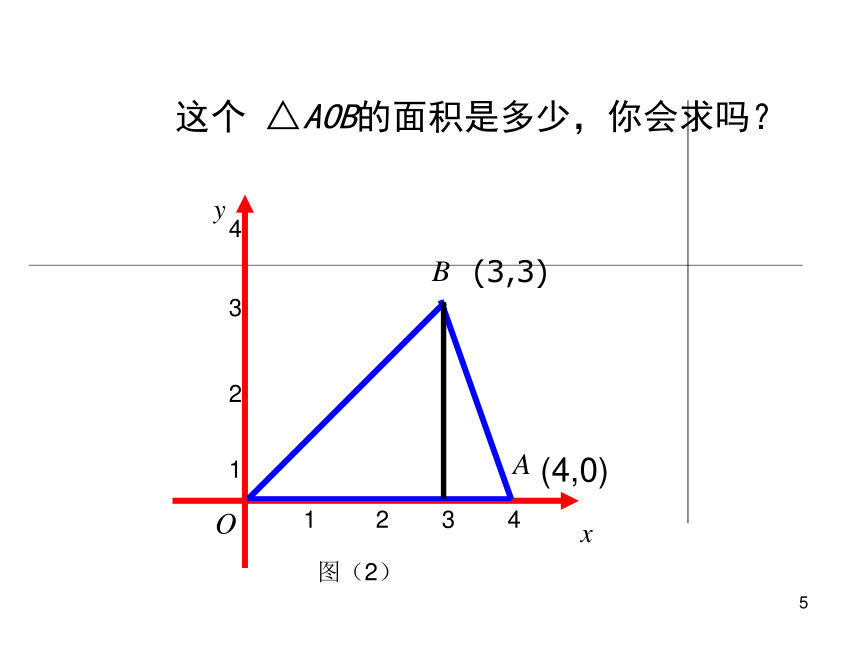
这个 △AOB的面积是多少,你会求吗?
y
O
x
图(2)
A
B
4
3
2
1
1 2 3 4
(3,3)
(4,0)
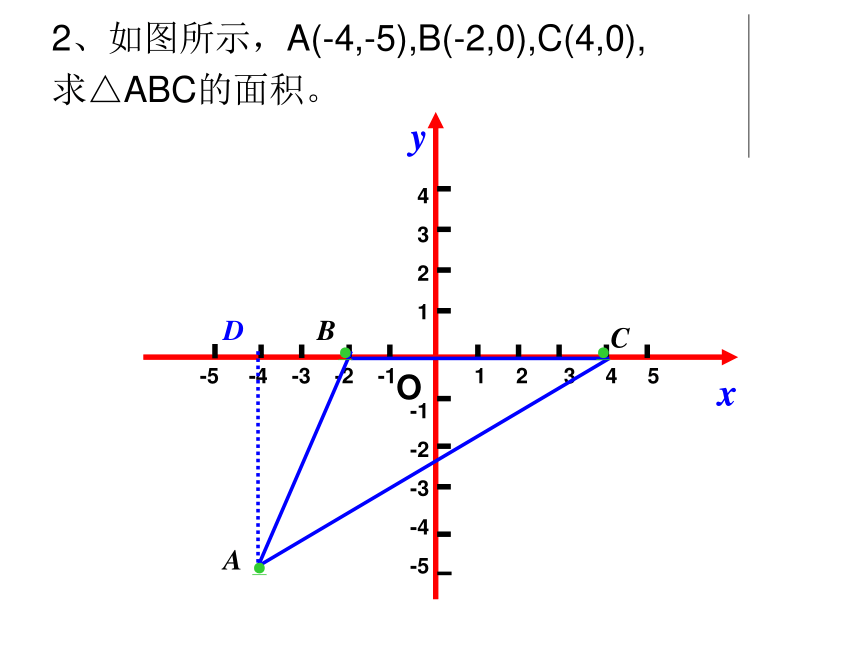
2、如图所示,A(-4,-5),B(-2,0),C(4,0),
求△ABC的面积。
O
x
y
-5 -4 -3 -2 -1 1 2 3 4 5
4
3
2
1
-1
-2
-3
-4
-5
A
B
C
●
●
●
D
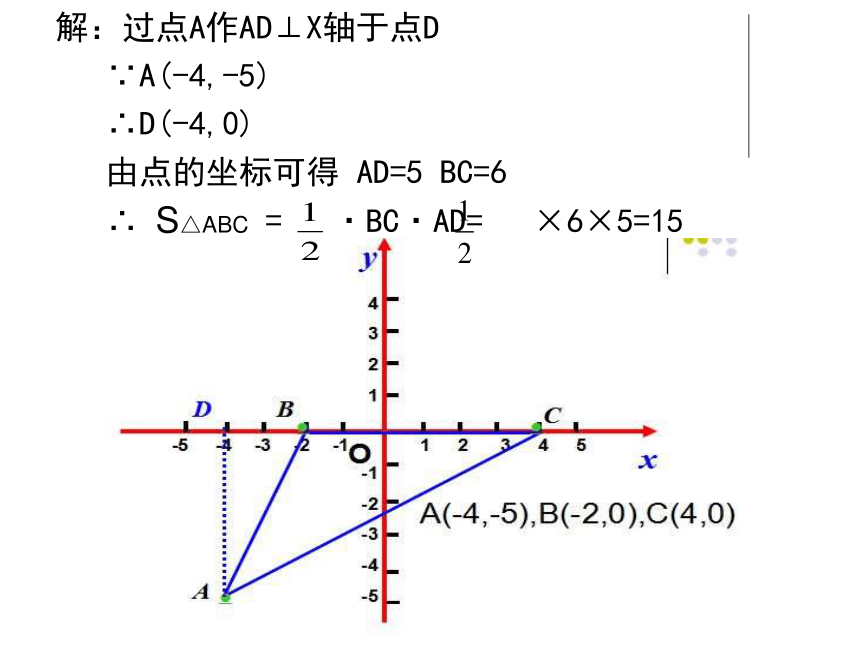
解:过点A作AD⊥X轴于点D
∵A(-4,-5)
∴D(-4,0)
由点的坐标可得 AD=5 BC=6
∴ S△ABC = ·BC·AD= ×6×5=15
*
y
A
B
C
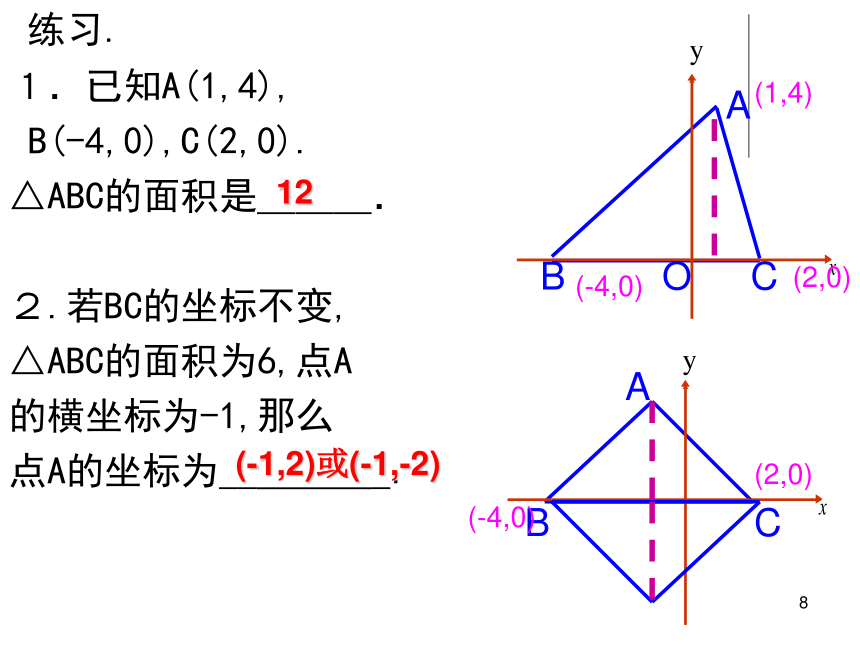
练习.
1.已知A(1,4),
B(-4,0),C(2,0).
△ABC的面积是___.
2.若BC的坐标不变,
△ABC的面积为6,点A
的横坐标为-1,那么
点A的坐标为__ _.
12
O
(1,4)
(-4,0)
(2,0)
C
y
A
B
(-4,0)
(2,0)
(-1,2)或(-1,-2)
*
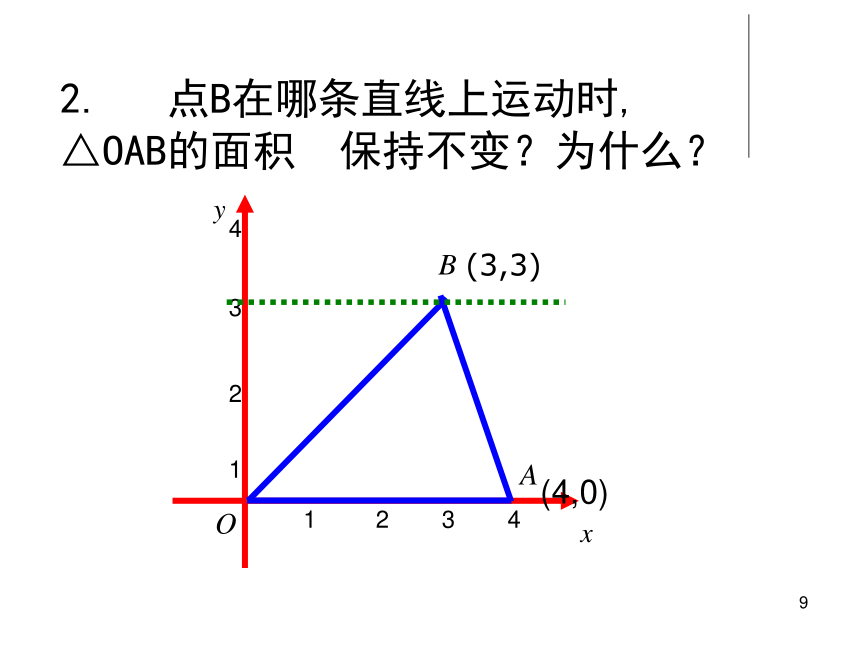
2. 点B在哪条直线上运动时, △OAB的面积 保持不变?为什么?
y
O
x
A
B
4
3
2
1
1 2 3 4
(3,3)
(4,0)
二:有一边与坐标轴平行
*
三角形ABC三个顶点的坐标分别为A(4,1),B(4,5),C(-1,2),求三角形ABC的面积.
题型三
割补法解决面积
*
三、探究展示
如图,四边形ABCO在平面直角坐标系中,
且A(1,4),B(5,2),C(6,0), O(0,0),
求四边形ABCO的面积。
O
x
y
-5 -4 -3 -2 -1 1 2 3 4 5
4
3
2
1
-1
-2
-3
-4
6
C
A
B
(1,4)
(6,0)
(5,2)
●
●
●
●
D
E
F
解:过点A作AD⊥X轴于点D,过点B作BE⊥X轴于点E
则D(1,0) E(5,0),由点的坐标可知
AD=4 BE=2 OD=1 DE=4 CE=1
∴ S四边形ABCD= S△AOD+ S梯形ABED+S△BEC
= OD·AD+ (BE+AD)·DE+ ·EC·BE
= ×1×4+ ×6×2+ ×1×2
= 15
三:探究展示
如图,四边形ABCO在平面直角坐标系中,
且A(1,4),B(5,2),C(6,0), O(0,0),
求四边形ABCO的面积。
O
x
y
-5 -4 -3 -2 -1 1 2 3 4 5
4
3
2
1
-1
-2
-3
-4
6
C
A
B
(1,4)
(6,0)
(5,2)
●
●
●
●
D
E
F
*
已知△ABC中,A(-1,-2),B(6,2),C(1,3),
求△ABC的面积.
y
-3
6
x
3
1
4
2
5
-2
-1
O
1
2
3
4
5
-2
-1
6
7
8
A(-1,-2)
B(6,2)
C(1,3)
*
-1
-2
x
y
1 2 3 4 5 6 7 8
5
4
3
2
1
-2 -1
O
A(-1,-2)
B(6,2)
C(1,3)
D(6,-2)
E(6,3)
F(-1,3)
方法1
*
-1
-2
x
y
1 2 3 4 5 6 7 8
5
4
3
2
1
-2 -1
O
A(-1,-2)
B(6,2)
C(1,3)
D(6,-2)
E(6,3)
方法2
*
-1
-2
x
y
1 2 3 4 5 6 7 8
5
4
3
2
1
-2 -1
O
A(-1,-2)
B(6,2)
C(1,3)
E(6,3)
F(-1,3)
方法3
*
练习1.三角形ABC三个顶点A、B、C的坐标分别为A(2,-1),B(1,-3),C(4,-3.5)。
1 2 3 4 5 6
-6
7
6
5
4
2
3
1
-1
-2
-3
-4
-5
-6
-7
-5
-4
-3
-2
-1
y
x
0
(1)把三角形A1B1C1向右平移4个单位,再向下平移3个单位,恰好得到三角形ABC,试写出三角形A1B1C1三个顶点的坐标;
A
C
B
*
1 2 3 4 5 6
-6
7
6
5
4
2
3
1
-1
-2
-3
-4
-5
-6
-7
-5
-4
-3
-2
-1
y
x
0
(2)求出三角形 A1B1C1的面积。
D
E
分析:可把它补成一个梯形减去
两个三角形。
*
1.等积变换
2.割补法求面积
谈谈我们的收获
化复杂为简单
化未知为已知
方法
转化
小结
一般的,在平面直角坐标系中,求已知顶点坐标地的多边形面积都可以通过割补的方法解决
平面直角坐标系中求面积
几种常见面积问题的求法
一、自主学习
1、(1)已知点P在x轴上,且到y轴的距离为2,
则 点P的坐标为__________
(2)已知点P到x轴的距离为3,到y轴的距离为4,则点P的坐标为_________________________
(3)若A(-1,0),B(4,0),则线段AB的长为____
(4)若A(0,5),B(0,3),则线段AB的长为_____
(5)若A(-3,-2),B(-5,-2),则线段AB的长为_____
(6)若A(3,2),B(3,-3),则线段AB的长为___
(-2,0)(2,0)
(4,3)(-4,3)(4,-3)(-4,-3)
5
2
2
5
题型一
底边在坐标轴上三角形面积的求法
*
*
如图(1), △AOB的面积是多少?
问题1
y
O
x
图(1)
A
B
4
3
2
1
1 2 3 4
(4,0)
(0,3)
*
这个 △AOB的面积是多少,你会求吗?
y
O
x
图(2)
A
B
4
3
2
1
1 2 3 4
(3,3)
(4,0)
2、如图所示,A(-4,-5),B(-2,0),C(4,0),
求△ABC的面积。
O
x
y
-5 -4 -3 -2 -1 1 2 3 4 5
4
3
2
1
-1
-2
-3
-4
-5
A
B
C
●
●
●
D
解:过点A作AD⊥X轴于点D
∵A(-4,-5)
∴D(-4,0)
由点的坐标可得 AD=5 BC=6
∴ S△ABC = ·BC·AD= ×6×5=15
*
y
A
B
C
练习.
1.已知A(1,4),
B(-4,0),C(2,0).
△ABC的面积是___.
2.若BC的坐标不变,
△ABC的面积为6,点A
的横坐标为-1,那么
点A的坐标为__ _.
12
O
(1,4)
(-4,0)
(2,0)
C
y
A
B
(-4,0)
(2,0)
(-1,2)或(-1,-2)
*
2. 点B在哪条直线上运动时, △OAB的面积 保持不变?为什么?
y
O
x
A
B
4
3
2
1
1 2 3 4
(3,3)
(4,0)
二:有一边与坐标轴平行
*
三角形ABC三个顶点的坐标分别为A(4,1),B(4,5),C(-1,2),求三角形ABC的面积.
题型三
割补法解决面积
*
三、探究展示
如图,四边形ABCO在平面直角坐标系中,
且A(1,4),B(5,2),C(6,0), O(0,0),
求四边形ABCO的面积。
O
x
y
-5 -4 -3 -2 -1 1 2 3 4 5
4
3
2
1
-1
-2
-3
-4
6
C
A
B
(1,4)
(6,0)
(5,2)
●
●
●
●
D
E
F
解:过点A作AD⊥X轴于点D,过点B作BE⊥X轴于点E
则D(1,0) E(5,0),由点的坐标可知
AD=4 BE=2 OD=1 DE=4 CE=1
∴ S四边形ABCD= S△AOD+ S梯形ABED+S△BEC
= OD·AD+ (BE+AD)·DE+ ·EC·BE
= ×1×4+ ×6×2+ ×1×2
= 15
三:探究展示
如图,四边形ABCO在平面直角坐标系中,
且A(1,4),B(5,2),C(6,0), O(0,0),
求四边形ABCO的面积。
O
x
y
-5 -4 -3 -2 -1 1 2 3 4 5
4
3
2
1
-1
-2
-3
-4
6
C
A
B
(1,4)
(6,0)
(5,2)
●
●
●
●
D
E
F
*
已知△ABC中,A(-1,-2),B(6,2),C(1,3),
求△ABC的面积.
y
-3
6
x
3
1
4
2
5
-2
-1
O
1
2
3
4
5
-2
-1
6
7
8
A(-1,-2)
B(6,2)
C(1,3)
*
-1
-2
x
y
1 2 3 4 5 6 7 8
5
4
3
2
1
-2 -1
O
A(-1,-2)
B(6,2)
C(1,3)
D(6,-2)
E(6,3)
F(-1,3)
方法1
*
-1
-2
x
y
1 2 3 4 5 6 7 8
5
4
3
2
1
-2 -1
O
A(-1,-2)
B(6,2)
C(1,3)
D(6,-2)
E(6,3)
方法2
*
-1
-2
x
y
1 2 3 4 5 6 7 8
5
4
3
2
1
-2 -1
O
A(-1,-2)
B(6,2)
C(1,3)
E(6,3)
F(-1,3)
方法3
*
练习1.三角形ABC三个顶点A、B、C的坐标分别为A(2,-1),B(1,-3),C(4,-3.5)。
1 2 3 4 5 6
-6
7
6
5
4
2
3
1
-1
-2
-3
-4
-5
-6
-7
-5
-4
-3
-2
-1
y
x
0
(1)把三角形A1B1C1向右平移4个单位,再向下平移3个单位,恰好得到三角形ABC,试写出三角形A1B1C1三个顶点的坐标;
A
C
B
*
1 2 3 4 5 6
-6
7
6
5
4
2
3
1
-1
-2
-3
-4
-5
-6
-7
-5
-4
-3
-2
-1
y
x
0
(2)求出三角形 A1B1C1的面积。
D
E
分析:可把它补成一个梯形减去
两个三角形。
*
1.等积变换
2.割补法求面积
谈谈我们的收获
化复杂为简单
化未知为已知
方法
转化
小结
一般的,在平面直角坐标系中,求已知顶点坐标地的多边形面积都可以通过割补的方法解决
