高中数学人教A版选修2-3第二章 2.4 正态分布课件(共32张PPT)
文档属性
| 名称 | 高中数学人教A版选修2-3第二章 2.4 正态分布课件(共32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 770.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-07 13:07:51 | ||
图片预览







文档简介
(共32张PPT)
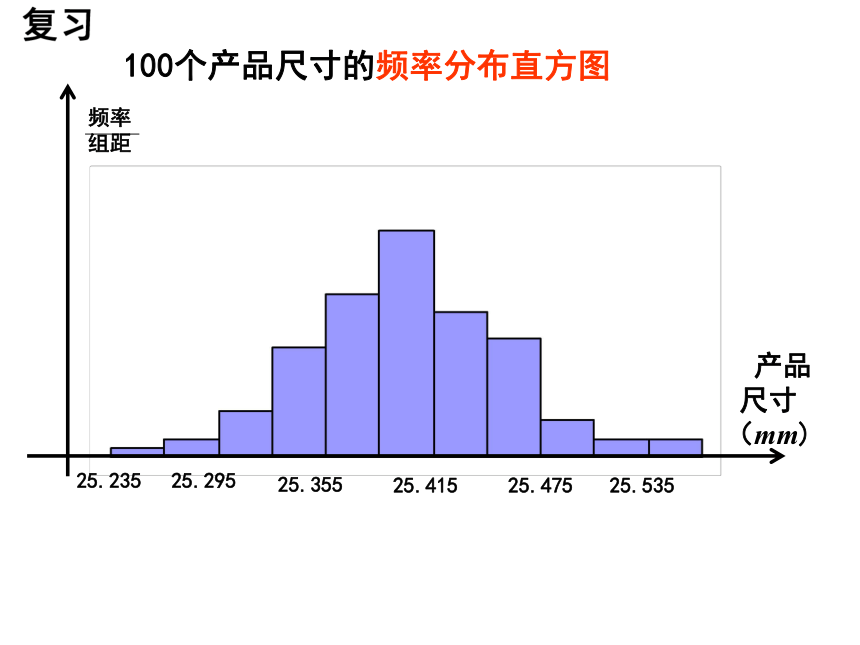
100个产品尺寸的频率分布直方图
25.235
25.295
25.355
25.415
25.475
25.535
产品
尺寸
(mm)
频率
组距
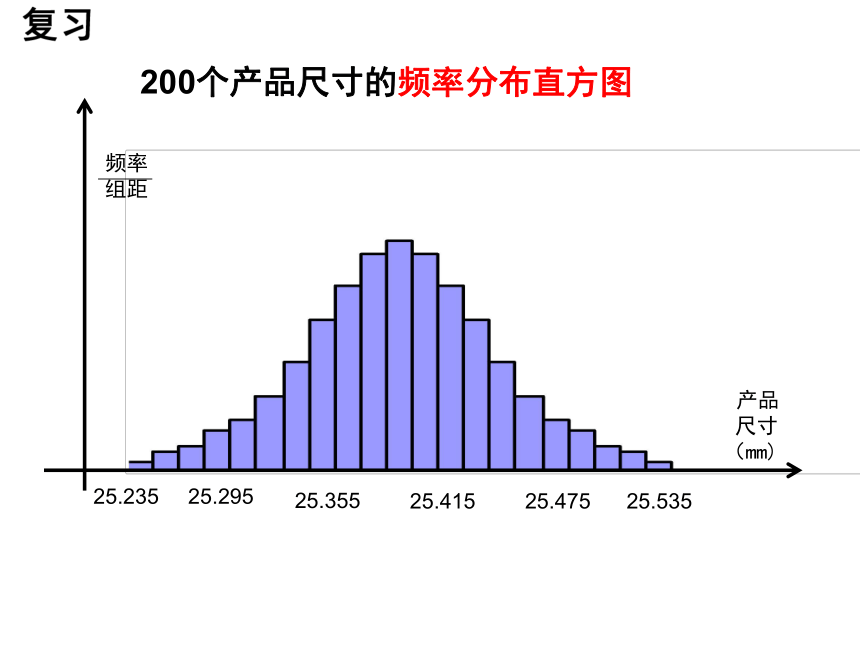
200个产品尺寸的频率分布直方图
25.235
25.295
25.355
25.415
25.475
25.535
产品
尺寸
(mm)
频率
组距
样本容量增大时
频率分布直方图
频率
组距
产品
尺寸
(mm)
产品
尺寸
(mm)
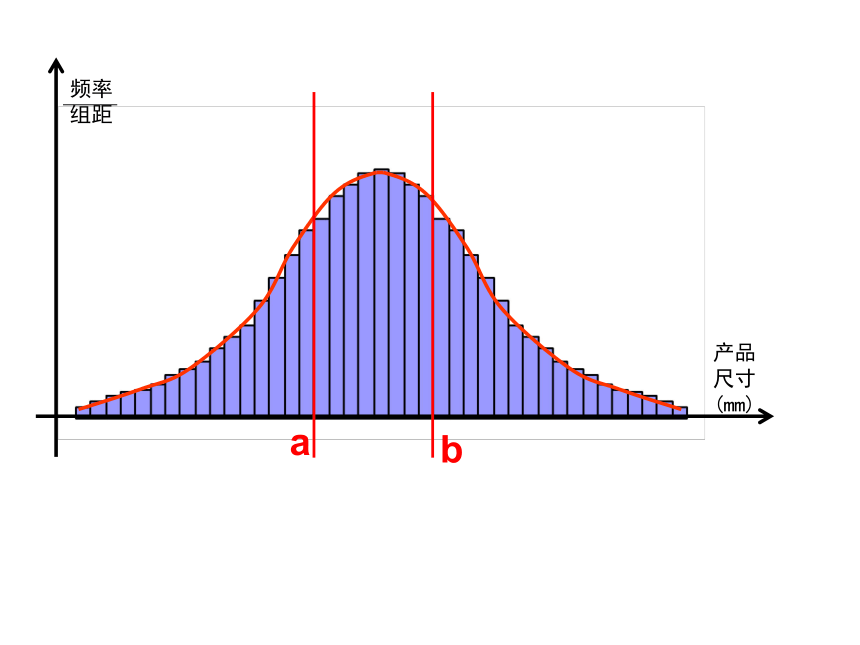
总体密度曲线
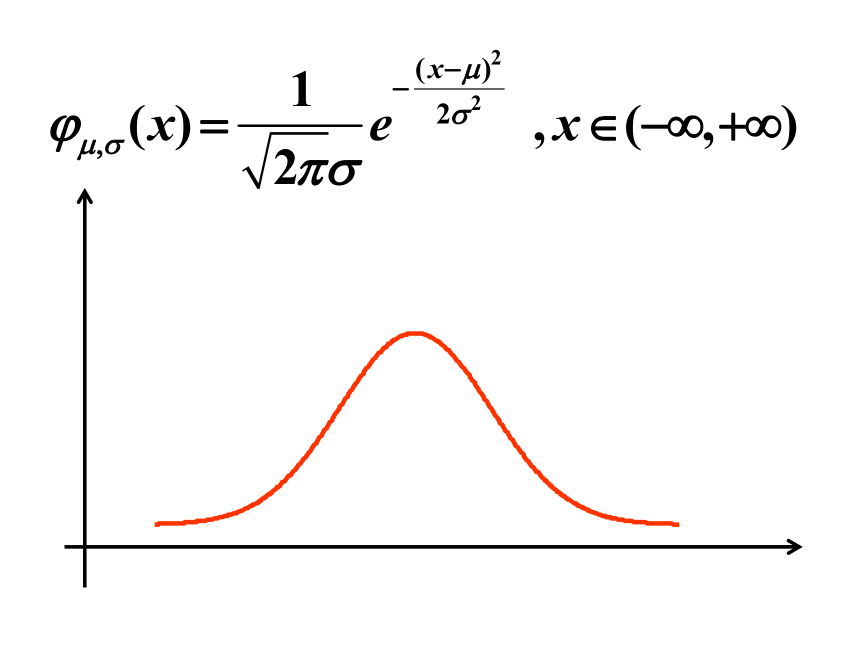
产品尺寸的总体密度曲线
就是或近似地是下面函数的图象:
频率
组距
产品
尺寸
(mm)
易知 x落在区间(a,b]的概率为:
x
y
一般地,如果对于任意实数 ,随机变量X
满足:
则称X的分布为正态分布,正态分布完全由
参数 确定,因此正态分布常记作
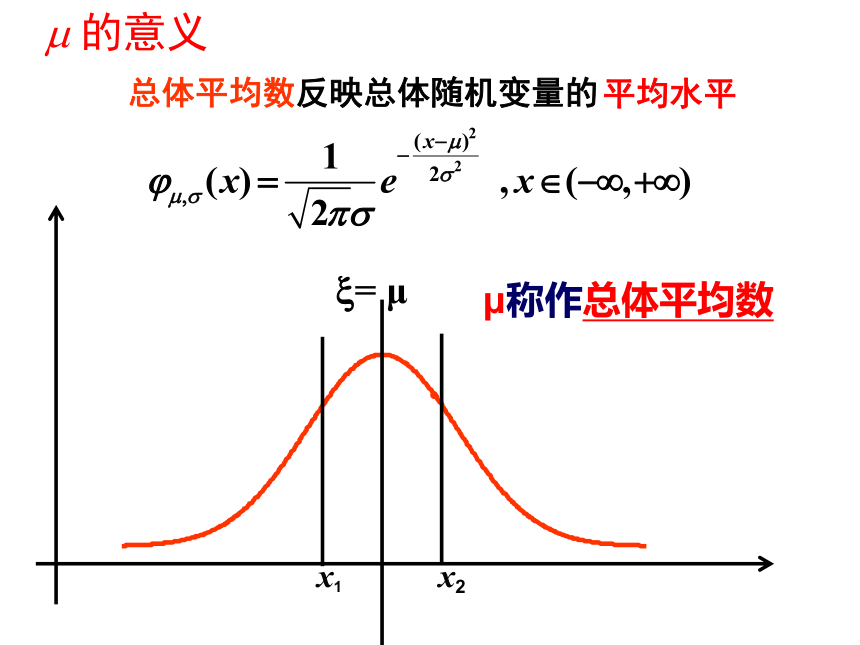
m 的意义
μ称作总体平均数
s的意义
正态曲线的函数表示式
m
例1:给出下列两个正态总体的函数表达式,请找出其均值μ和标准差σ。
(1)
(2)
(3)
(-∞<x<+∞
例3.设随机变量ζ~N(2,4),则D( )等于
(A)1 (B)2
(C)0.5 (D)4
练习:
把一个正态曲线a沿着横轴方向向右移动2个
单位,得到一个新的曲线b,下列说法不正确的是
(A)曲线b仍然是正态曲线
(B)曲线a和曲线b的最高点的纵坐标相等
(C)以曲线a为概率密度曲线的总体的方差比
以曲线b为概率密度曲线的总体的方差大2
(D)以曲线a为概率密度曲线的总体的期望比
以曲线b为概率密度曲线的总体的期望小2
正态曲线
具有两头低、中间高、左右对称的基本特征
(1)曲线在x轴的上方,与x轴不相交.
(2)曲线是单峰的,它关于直线x=μ对称.
正态曲线的性质
(4)曲线与x轴之间的面积为1
σ=0.5
0
1
2
-1
-2
x
y
-3
3
X=μ
σ=1
σ=2
(6)当μ一定时,曲线的形状由σ确定 .
σ越大,曲线越“矮胖”,表示总体的分布越分散;
σ越小,曲线越“瘦高”,表示总体的分布越集中.
(5)当 x<μ时,曲线上升;当x>μ时,曲线下降.并且当曲线向左、右两边无限延伸时,以x轴为渐近线,向它无限靠近.
正态曲线的性质
方差相等、均数不等的正态分布图示
σ=0.5
μ= -1
μ=0
μ= 1
均数相等、方差不等的正态分布图示
?
?=1
μ=0
由于这些概率值很小(一般不超过5 % ),通常称这些情况发生为小概率事件。
即事件在一次试验中几乎不可能发生。
特殊区间的概率:
m-a
m+a
x=μ
正态曲线下的面积规律
-4 -3 -2 -1 0 1 2 3 4
?-3? ?-2? ?-? ? ?+? ?+2? ?+3?
S(-?, ?-3?)=0.0013
S(-?, ?-2?)=0.0228
S(-?, ?-1?)=0.1587
S(-?, ?)=0.5
S(-?, ?+3?)=0.9987
S(-?, ?+2?)=0.9772
S(-?, ?+1?)=0.6587
S(-?, ?)=1
例4. 求标准正态总体在(-1,2)内取值的概率.
例5:某厂生产的圆柱形零件的外直径ξ服从正态分布 ,质检人员从该厂生产的1000件零件中随机抽查一件, 测得它的外直径为5.7cm,试问该厂生产的这批零件是否合格?
解:
这说明在一次试验中,出现了几乎不可能发生的小概率事件.
据此可认为该批零件是不合格的。
练习
(1)若随机变量ζ~N(1,0.25),则2ζ的概率密度函数为 .
(2)期望为2,方差 为的正态分布的密度
函数是 .
(3)已知正态总体落在区间(0.2,+∞)的概率是0.5,则相应的正态曲线f(x)在x= 时,达到最高点.
(4)已知ζ~N(0,1),P(ζ≤1.96)=Ф(1.96)=
0.9750,则Ф(-1.96)= .
100个产品尺寸的频率分布直方图
25.235
25.295
25.355
25.415
25.475
25.535
产品
尺寸
(mm)
频率
组距
200个产品尺寸的频率分布直方图
25.235
25.295
25.355
25.415
25.475
25.535
产品
尺寸
(mm)
频率
组距
样本容量增大时
频率分布直方图
频率
组距
产品
尺寸
(mm)
产品
尺寸
(mm)
总体密度曲线
产品尺寸的总体密度曲线
就是或近似地是下面函数的图象:
频率
组距
产品
尺寸
(mm)
易知 x落在区间(a,b]的概率为:
x
y
一般地,如果对于任意实数 ,随机变量X
满足:
则称X的分布为正态分布,正态分布完全由
参数 确定,因此正态分布常记作
m 的意义
μ称作总体平均数
s的意义
正态曲线的函数表示式
m
例1:给出下列两个正态总体的函数表达式,请找出其均值μ和标准差σ。
(1)
(2)
(3)
(-∞<x<+∞
例3.设随机变量ζ~N(2,4),则D( )等于
(A)1 (B)2
(C)0.5 (D)4
练习:
把一个正态曲线a沿着横轴方向向右移动2个
单位,得到一个新的曲线b,下列说法不正确的是
(A)曲线b仍然是正态曲线
(B)曲线a和曲线b的最高点的纵坐标相等
(C)以曲线a为概率密度曲线的总体的方差比
以曲线b为概率密度曲线的总体的方差大2
(D)以曲线a为概率密度曲线的总体的期望比
以曲线b为概率密度曲线的总体的期望小2
正态曲线
具有两头低、中间高、左右对称的基本特征
(1)曲线在x轴的上方,与x轴不相交.
(2)曲线是单峰的,它关于直线x=μ对称.
正态曲线的性质
(4)曲线与x轴之间的面积为1
σ=0.5
0
1
2
-1
-2
x
y
-3
3
X=μ
σ=1
σ=2
(6)当μ一定时,曲线的形状由σ确定 .
σ越大,曲线越“矮胖”,表示总体的分布越分散;
σ越小,曲线越“瘦高”,表示总体的分布越集中.
(5)当 x<μ时,曲线上升;当x>μ时,曲线下降.并且当曲线向左、右两边无限延伸时,以x轴为渐近线,向它无限靠近.
正态曲线的性质
方差相等、均数不等的正态分布图示
σ=0.5
μ= -1
μ=0
μ= 1
均数相等、方差不等的正态分布图示
?
?=1
μ=0
由于这些概率值很小(一般不超过5 % ),通常称这些情况发生为小概率事件。
即事件在一次试验中几乎不可能发生。
特殊区间的概率:
m-a
m+a
x=μ
正态曲线下的面积规律
-4 -3 -2 -1 0 1 2 3 4
?-3? ?-2? ?-? ? ?+? ?+2? ?+3?
S(-?, ?-3?)=0.0013
S(-?, ?-2?)=0.0228
S(-?, ?-1?)=0.1587
S(-?, ?)=0.5
S(-?, ?+3?)=0.9987
S(-?, ?+2?)=0.9772
S(-?, ?+1?)=0.6587
S(-?, ?)=1
例4. 求标准正态总体在(-1,2)内取值的概率.
例5:某厂生产的圆柱形零件的外直径ξ服从正态分布 ,质检人员从该厂生产的1000件零件中随机抽查一件, 测得它的外直径为5.7cm,试问该厂生产的这批零件是否合格?
解:
这说明在一次试验中,出现了几乎不可能发生的小概率事件.
据此可认为该批零件是不合格的。
练习
(1)若随机变量ζ~N(1,0.25),则2ζ的概率密度函数为 .
(2)期望为2,方差 为的正态分布的密度
函数是 .
(3)已知正态总体落在区间(0.2,+∞)的概率是0.5,则相应的正态曲线f(x)在x= 时,达到最高点.
(4)已知ζ~N(0,1),P(ζ≤1.96)=Ф(1.96)=
0.9750,则Ф(-1.96)= .
