4.3.1 利用边边边判定三角形全等课课练(含答案)
文档属性
| 名称 | 4.3.1 利用边边边判定三角形全等课课练(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-05 18:13:53 | ||
图片预览

文档简介
北师大版数学七年级下册﹒同步课时训练
第四章 三角形
3 探索三角形全等的条件
第1课时 利用边边边判定三角形全等
一、选择题
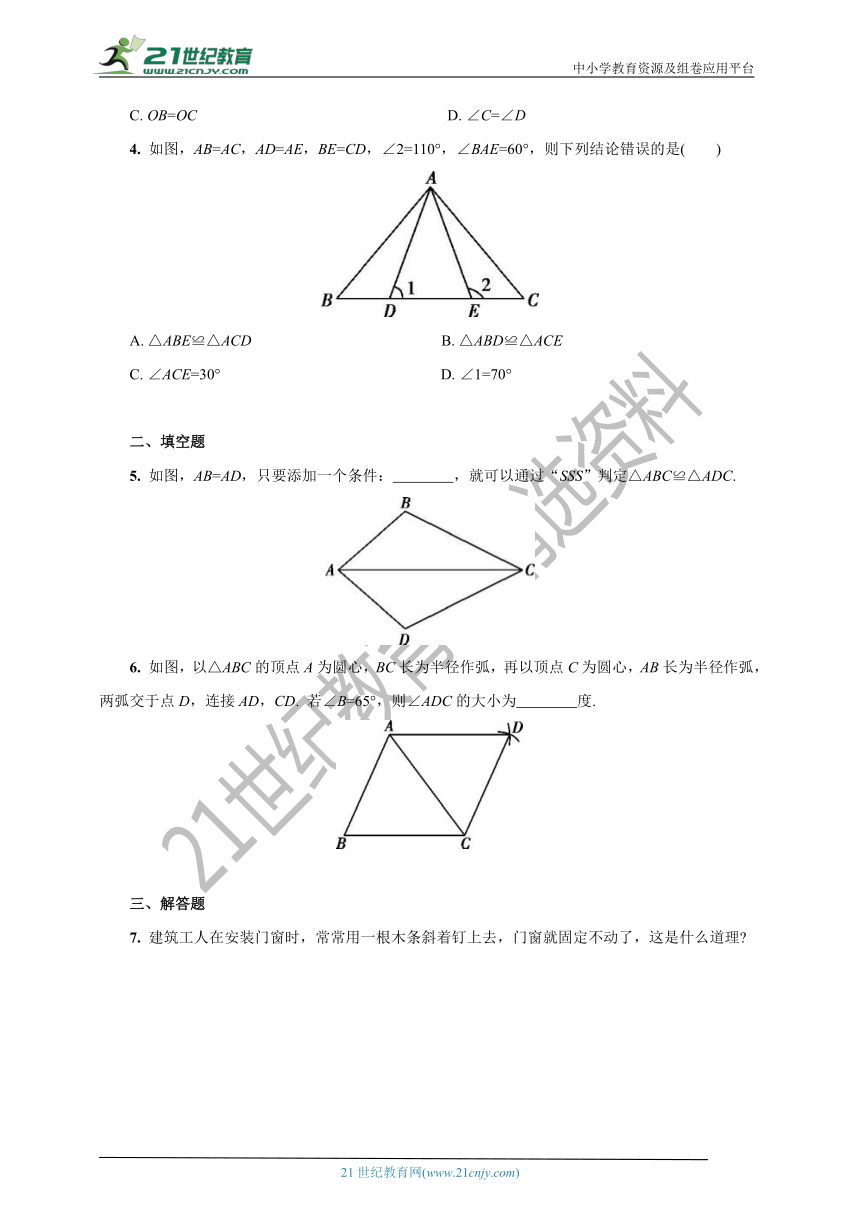
1. 如图,AB=AC,BD=CD,则可推出( )
A. △BAD≌△BCD B. △ABD≌△ACD
C. △ACD≌△BCD D. △ACE≌△BDE
2. 如图,在四边形ABCD中,E是BC的中点,连接AC,AE,若AB=AC,AE=CD,AD=CE,则图中的全等三角形有( )
A. 0对 B. 1对 C. 2对 D. 3对
3. 如图,线段AD与BC相交于点O,连接AB,AC,BD,若AC=BD,AD=BC,则下列结论中不正确的是( )
A. △ABC≌△BAD B. ∠CAB=∠DBA
C. OB=OC D. ∠C=∠D
4. 如图,AB=AC,AD=AE,BE=CD,∠2=110°,∠BAE=60°,则下列结论错误的是( )
A. △ABE≌△ACD B. △ABD≌△ACE
C. ∠ACE=30° D. ∠1=70°
二、填空题
5. 如图,AB=AD,只要添加一个条件: ,就可以通过“SSS”判定△ABC≌△ADC.?
6. 如图,以△ABC的顶点A为圆心,BC长为半径作弧,再以顶点C为圆心,AB长为半径作弧,两弧交于点D,连接AD,CD. 若∠B=65°,则∠ADC的大小为 度.?
三、解答题
7. 建筑工人在安装门窗时,常常用一根木条斜着钉上去,门窗就固定不动了,这是什么道理?
8. 如图所示,已知∠BAC=∠DAE,AB=AC,AD=AE,BD=CE,∠1=25°,∠2=30°,求∠3的度数.
9. 如图,在△ABC中,AC=BC,D是AB上的一点,AE⊥CD交CD的延长线于点E,BF⊥CD于点F,若CE=BF,AE=EF+BF.试判断直线AC与BC的位置关系,并说明理由.
参 考 答 案
1. B 2. D 3. C 4. C
5. BC=DC
6. 65
7. 解:因为门窗是四边形,四边形具有不稳定性,易松动.斜钉一根木条就构成了三角形,而三角形具有稳定性,所以门窗就固定不动了.
8. 解:在△BAD和△CAE中,∴△BAD≌△CAE(SSS),∴∠ABD=∠2=30°,∵∠1=25°,∴∠3=∠1+∠ABD=25°+30°=55°(由三角形内角和定理与平角的定义可得∠3=∠1+∠ABD).
9. 解:AC⊥BC,理由如下:∵CE=BF,AE=EF+BF,CF=EF+CE,∴AE=CF. 在△ACE和△CBF中, ∴△ACE≌△CBF(SSS),∴∠CAE=∠BCF. 在Rt△ACE中,∵∠CAE+∠ACE=90°,∴∠ACE+∠BCF=90°,∴AC⊥BC.
第四章 三角形
3 探索三角形全等的条件
第1课时 利用边边边判定三角形全等
一、选择题
1. 如图,AB=AC,BD=CD,则可推出( )
A. △BAD≌△BCD B. △ABD≌△ACD
C. △ACD≌△BCD D. △ACE≌△BDE
2. 如图,在四边形ABCD中,E是BC的中点,连接AC,AE,若AB=AC,AE=CD,AD=CE,则图中的全等三角形有( )
A. 0对 B. 1对 C. 2对 D. 3对
3. 如图,线段AD与BC相交于点O,连接AB,AC,BD,若AC=BD,AD=BC,则下列结论中不正确的是( )
A. △ABC≌△BAD B. ∠CAB=∠DBA
C. OB=OC D. ∠C=∠D
4. 如图,AB=AC,AD=AE,BE=CD,∠2=110°,∠BAE=60°,则下列结论错误的是( )
A. △ABE≌△ACD B. △ABD≌△ACE
C. ∠ACE=30° D. ∠1=70°
二、填空题
5. 如图,AB=AD,只要添加一个条件: ,就可以通过“SSS”判定△ABC≌△ADC.?
6. 如图,以△ABC的顶点A为圆心,BC长为半径作弧,再以顶点C为圆心,AB长为半径作弧,两弧交于点D,连接AD,CD. 若∠B=65°,则∠ADC的大小为 度.?
三、解答题
7. 建筑工人在安装门窗时,常常用一根木条斜着钉上去,门窗就固定不动了,这是什么道理?
8. 如图所示,已知∠BAC=∠DAE,AB=AC,AD=AE,BD=CE,∠1=25°,∠2=30°,求∠3的度数.
9. 如图,在△ABC中,AC=BC,D是AB上的一点,AE⊥CD交CD的延长线于点E,BF⊥CD于点F,若CE=BF,AE=EF+BF.试判断直线AC与BC的位置关系,并说明理由.
参 考 答 案
1. B 2. D 3. C 4. C
5. BC=DC
6. 65
7. 解:因为门窗是四边形,四边形具有不稳定性,易松动.斜钉一根木条就构成了三角形,而三角形具有稳定性,所以门窗就固定不动了.
8. 解:在△BAD和△CAE中,∴△BAD≌△CAE(SSS),∴∠ABD=∠2=30°,∵∠1=25°,∴∠3=∠1+∠ABD=25°+30°=55°(由三角形内角和定理与平角的定义可得∠3=∠1+∠ABD).
9. 解:AC⊥BC,理由如下:∵CE=BF,AE=EF+BF,CF=EF+CE,∴AE=CF. 在△ACE和△CBF中, ∴△ACE≌△CBF(SSS),∴∠CAE=∠BCF. 在Rt△ACE中,∵∠CAE+∠ACE=90°,∴∠ACE+∠BCF=90°,∴AC⊥BC.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
