北师大版八年级数学上册5.7用二元一次方程组确定一次函数表达式课件(共19张PPT)
文档属性
| 名称 | 北师大版八年级数学上册5.7用二元一次方程组确定一次函数表达式课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 522.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-06 19:23:10 | ||
图片预览






文档简介
(共19张PPT)
【义务教育教科书北师版八年级上册】
第五章 二元一次方程组
7 用二元一次方程组
确定一次函数表达式
一、温故启新
二元一次方程(组)与一次函数有哪些联系?
1、以一个二元一次方程的解为坐标的点组成的图象与相应的一次函数的图象 ,是 ;
2、确定两条直线交点的坐标,相当于求相应的二元一次方程组的 ,解一个二元一次方程组相当于确定相应两条直线 。
相同
一条直线
解
交点坐标
二、学习目标:
1.掌握利用二元一次方程组确定一次函数的表达式
2.进一步理解二元一次方程(组)与 一次函数之间的联系
1.若一次函数y=-2x+b经过点(3,1),则该函
数的表达式为 .
2.已知A(1,2)和点B(-2,5),试写出一个
一次函数,使它的图象经过A、B两点。
解:设经过A、B两点的一次函数为 ,
分别把A(1,2)和B(-2,5)代入得
解得 k=
b=
所以这个一次函数的表达式为
,
.
y=kx+b
k+b=2
-2k+b=5
-1
3
y=-x+3
y=-2x+7
三、自学检测
1. A、B两地相距100 km,甲、乙两人骑自行车分别从A、B两地相向而行。假设他们都保持匀速行驶,则他们各自到A地的距离 s(km)都是骑车时间 t (h)的一次函数.
1 h后乙距A地80 km,
2 h后甲距A地 30 km.
问:经过多长时间两人相遇 ?
四、学习新知
你有几种解决上述问题的方法?它们有什么不同之处?
0
4
1
2
3
l1
l2
t
s
100
80
60
40
20
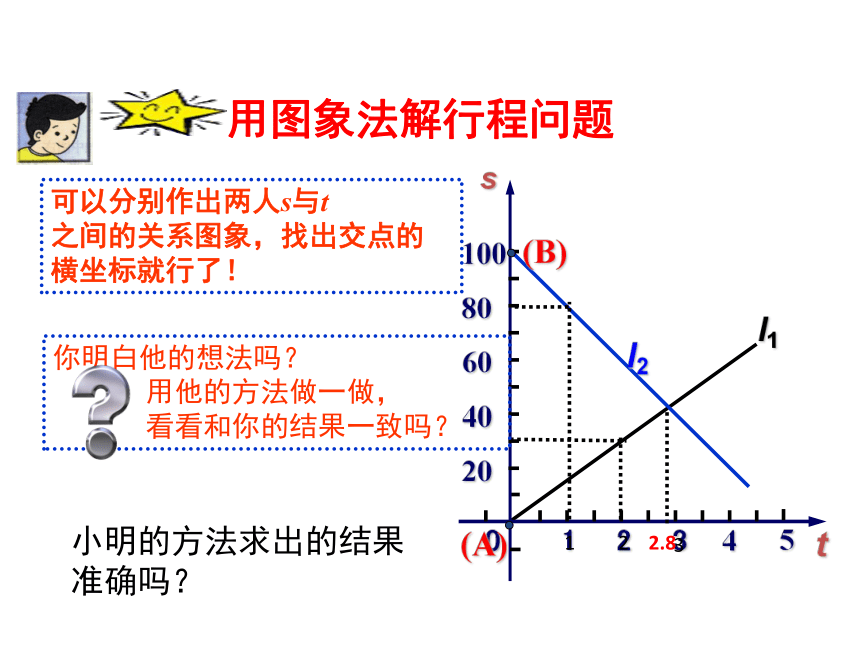
用图象法解行程问题
(A)
(B)
可以分别作出两人s与t
之间的关系图象,找出交点的横坐标就行了!
小明的方法求出的结果准确吗?
1
2
3
5
2.8
你明白他的想法吗?
用他的方法做一做,
看看和你的结果一致吗?
用方程解行程问题
小亮
1 h后乙距A地80 km,即乙的速度是 20 km/h,
2 h后甲距A地 30 km,故甲的速度是 15km/h,
由此可求出甲、乙两人的速度, 以及……
?t≈2.86
你明白他的想法吗?
用他的方法做一做,
看看和你的结果一致吗?
设同时出发后t时相遇,则
15t+20t=100
读《苦儿流浪记》有感
作者:朱雨桐
在这个多姿多彩的寒假生活中,我读了许多触动人心的世界文学名著,如下:《苦儿流浪记》、《会飞的教室》、《简爱》、《洋葱头历险记》、《百万英镑》等,其中让我感触最深的是《苦儿流浪记》这本书。
这本书的主人公是一位弃儿,他叫雷米,年仅六个月的雷米就被他的叔叔悄悄抱走,丢弃在巴黎街头,然后等着好心人来抱走他,雷米的叔叔之所以这样做,为的就是霸占侄儿的财产,好心的巴伯兰把雷米捡回了家,一把屎一把尿地把雷米拉扯到八岁大时,又背着他的妻子将雷米卖给了一位有着神秘身世的江湖一人——维泰利斯,从此雷米开始了他的流浪生涯,在这期间,雷米还遇到了许多糟糕透顶的坏事,幸亏雷米福大命大,一一摆脱了这些困境:在矿井里遇到洪水的袭击,差点命丧于此;因饥寒交迫,雷米和维泰利斯躲到花农门前,险些死去……
总而言之雷米凭着他坚定不移的信念最终战胜了困难,大概上帝被雷米的毅力和勇敢给感动了,终于伸出援助之手,帮雷米找到并回到他的生母身边。
当我读完《苦儿流浪记》这本书时,我忽然悟出了一个道理:困难像弹簧,你弱它就强,你强它就弱,面对困难时,你千
万不要怕他,因为你越怕它,它就越强,越困难
求出s与t之间的关系式,联立解方程组
对于乙,s是t的一次函数,可设 s=kt+b。
当t=0时,s=100;当t=1时,s=80。
将它们分别代入s=kt+b中,可以求出k、b的值,
也即可以求出乙s与t之间的函数表达式。
同样可求出甲s与t之间的函数表达式。
再联立这两个表达式,求解方程组就行了。
小颖
提示
消去 s
你明白他的想法吗?
用他的方法做一做,
看看和你的结果一致吗?
议一议
(1)对照教材,比较你的做法与小明,小亮与小颖的方法有什么不同?与同伴交流
(2)思考讨论:图象法与代数法在解决问题时有什么不同?
用作图象的方法可以直观地获得问题的结果,但有时却难以准确,为了获得准确的结果,我们一般用代数方法。
2. 例:某长途汽车客运站规定,乘客可以免费携带一定质量的行李,但超过该质量则需购买行李票,且行李费y(元)是行李质量x(kg)的一次函数,现知李明带了60kg的行李,交了行李费5元,王华带了90kg的行李,交了行李费10元.
(1)写出y与x之间的函数表达式
(2)旅客最多可免费携带多少千克的行李?
解:(1)设y=kx+b,根据题意,得
解得
所以 y与x之间的函数表达式为
(2)当y=0时,
解得x=30
所以旅客最多可以免
费携带30 kg的行李。
学习新知
(1)一般设一次函数的表达式为什么?
(2)确定一次函数的表达式关键是确定哪些参数的值?
(3)确定一次函数的表达式需要几个条件?
(4)确定一次函数的表达式需要几个步骤?
2. 例:某长途汽车客运站规定,乘客可以免费携带一定质量的行李,但超过该质量则需购买行李票,且行李费y(元)是行李质量x(kg)的一次函数,现知李明带了60kg的行李,交了行李费5元,王华带了90kg的行李,交了行李费10元.
(1)写出y与x之间的函数表达式
(2)旅客最多可免费携带多少千克的行李?
解:(1)设y=kx+b,根据题意,得
解得
所以 y与x之间的函数表达式为
(2)当y=0时,
解得x=30
所以旅客最多可以免
费携带30 kg的行李。
学习新知
2、利用待定系数法求一次函数表达式的主要步骤如下:
(1)设出函数表达式: y=kx+b;
(2)把已知条件代入,得到关于k、b的方程组;
(3)解方程组,求出k、b的值;
(4)写出其表达式.
知识升华
1、像本例这样,先设出函数表达式,再根据所给条件确定表达式中未知数的系数,从而得到函数表达式的方法,叫做待定系数法.
1.在弹性限度内,弹簧的长度y(cm)是所挂物体质量x(kg)的一次函数.当所挂物体的质量为1kg时,弹簧长15cm;当所挂物体的质量为3kg时,弹簧长16cm.写出y与x之间的关系式,并求当所挂物体的质量为4kg时弹簧的长度.
解:(1)设y=kx+b,根据题意,得
解得
∴y与x之间的函数表达式为
(2)当x=4时,
y=0.5×4+14.5
解得y=16.5
∴当所挂物体的质量
为4kg时弹簧的长为16.5cm.
五、课内训练(一)
2.图中的两条直线 , 的交点坐标是 ,
、
可以看作方程组 的解。
解:设直线 的解析式为 y=k1x+b1,
分别把( , )和( , )代入得
设直线 的解析式为 y=k2x+b2,
分别把( , )和( , )代入得
课内训练(二)——精英园地
2.图中的两条直线 , 的交点坐标是 ,
它可以看作方程组 的解。
解:设直线 的解析式为 y=k1x+b1,
分别把( 0 , 1 )和( 1 , 3 )代入得
解得
∴直线 的解析式为 y=2x+1
设直线 的解析式为 y=k2x+b2,
分别把( 0 , 4 )和( 1 , 3 )代入得
解得
∴直线 的解析式为 y=-x+4
∴这交点可以看成是
的解
七、课堂小结
谈谈本节课你的收获与感受
八、检测反馈
x -2 0 1
y 3 p 0
1.一次函数y=kx+b经过点(1,1),(2,- 4),则k与b的值为( )
2.根据下表中一次函数的自变量x与函数y的部分对应值,可得p的值为( )
A.1 B.-1 C.3 D.-3
3.已知函数y=2x+b的图象经过点(a, 7)和(-2,a),求这个函数表达式。
九、作业布置
A组:P128问题解决 1,2
B组:
已知点A(1,2)B(2,-3)C(3,-4),问A,B,C三点在同一直线吗?
【义务教育教科书北师版八年级上册】
第五章 二元一次方程组
7 用二元一次方程组
确定一次函数表达式
一、温故启新
二元一次方程(组)与一次函数有哪些联系?
1、以一个二元一次方程的解为坐标的点组成的图象与相应的一次函数的图象 ,是 ;
2、确定两条直线交点的坐标,相当于求相应的二元一次方程组的 ,解一个二元一次方程组相当于确定相应两条直线 。
相同
一条直线
解
交点坐标
二、学习目标:
1.掌握利用二元一次方程组确定一次函数的表达式
2.进一步理解二元一次方程(组)与 一次函数之间的联系
1.若一次函数y=-2x+b经过点(3,1),则该函
数的表达式为 .
2.已知A(1,2)和点B(-2,5),试写出一个
一次函数,使它的图象经过A、B两点。
解:设经过A、B两点的一次函数为 ,
分别把A(1,2)和B(-2,5)代入得
解得 k=
b=
所以这个一次函数的表达式为
,
.
y=kx+b
k+b=2
-2k+b=5
-1
3
y=-x+3
y=-2x+7
三、自学检测
1. A、B两地相距100 km,甲、乙两人骑自行车分别从A、B两地相向而行。假设他们都保持匀速行驶,则他们各自到A地的距离 s(km)都是骑车时间 t (h)的一次函数.
1 h后乙距A地80 km,
2 h后甲距A地 30 km.
问:经过多长时间两人相遇 ?
四、学习新知
你有几种解决上述问题的方法?它们有什么不同之处?
0
4
1
2
3
l1
l2
t
s
100
80
60
40
20
用图象法解行程问题
(A)
(B)
可以分别作出两人s与t
之间的关系图象,找出交点的横坐标就行了!
小明的方法求出的结果准确吗?
1
2
3
5
2.8
你明白他的想法吗?
用他的方法做一做,
看看和你的结果一致吗?
用方程解行程问题
小亮
1 h后乙距A地80 km,即乙的速度是 20 km/h,
2 h后甲距A地 30 km,故甲的速度是 15km/h,
由此可求出甲、乙两人的速度, 以及……
?t≈2.86
你明白他的想法吗?
用他的方法做一做,
看看和你的结果一致吗?
设同时出发后t时相遇,则
15t+20t=100
读《苦儿流浪记》有感
作者:朱雨桐
在这个多姿多彩的寒假生活中,我读了许多触动人心的世界文学名著,如下:《苦儿流浪记》、《会飞的教室》、《简爱》、《洋葱头历险记》、《百万英镑》等,其中让我感触最深的是《苦儿流浪记》这本书。
这本书的主人公是一位弃儿,他叫雷米,年仅六个月的雷米就被他的叔叔悄悄抱走,丢弃在巴黎街头,然后等着好心人来抱走他,雷米的叔叔之所以这样做,为的就是霸占侄儿的财产,好心的巴伯兰把雷米捡回了家,一把屎一把尿地把雷米拉扯到八岁大时,又背着他的妻子将雷米卖给了一位有着神秘身世的江湖一人——维泰利斯,从此雷米开始了他的流浪生涯,在这期间,雷米还遇到了许多糟糕透顶的坏事,幸亏雷米福大命大,一一摆脱了这些困境:在矿井里遇到洪水的袭击,差点命丧于此;因饥寒交迫,雷米和维泰利斯躲到花农门前,险些死去……
总而言之雷米凭着他坚定不移的信念最终战胜了困难,大概上帝被雷米的毅力和勇敢给感动了,终于伸出援助之手,帮雷米找到并回到他的生母身边。
当我读完《苦儿流浪记》这本书时,我忽然悟出了一个道理:困难像弹簧,你弱它就强,你强它就弱,面对困难时,你千
万不要怕他,因为你越怕它,它就越强,越困难
求出s与t之间的关系式,联立解方程组
对于乙,s是t的一次函数,可设 s=kt+b。
当t=0时,s=100;当t=1时,s=80。
将它们分别代入s=kt+b中,可以求出k、b的值,
也即可以求出乙s与t之间的函数表达式。
同样可求出甲s与t之间的函数表达式。
再联立这两个表达式,求解方程组就行了。
小颖
提示
消去 s
你明白他的想法吗?
用他的方法做一做,
看看和你的结果一致吗?
议一议
(1)对照教材,比较你的做法与小明,小亮与小颖的方法有什么不同?与同伴交流
(2)思考讨论:图象法与代数法在解决问题时有什么不同?
用作图象的方法可以直观地获得问题的结果,但有时却难以准确,为了获得准确的结果,我们一般用代数方法。
2. 例:某长途汽车客运站规定,乘客可以免费携带一定质量的行李,但超过该质量则需购买行李票,且行李费y(元)是行李质量x(kg)的一次函数,现知李明带了60kg的行李,交了行李费5元,王华带了90kg的行李,交了行李费10元.
(1)写出y与x之间的函数表达式
(2)旅客最多可免费携带多少千克的行李?
解:(1)设y=kx+b,根据题意,得
解得
所以 y与x之间的函数表达式为
(2)当y=0时,
解得x=30
所以旅客最多可以免
费携带30 kg的行李。
学习新知
(1)一般设一次函数的表达式为什么?
(2)确定一次函数的表达式关键是确定哪些参数的值?
(3)确定一次函数的表达式需要几个条件?
(4)确定一次函数的表达式需要几个步骤?
2. 例:某长途汽车客运站规定,乘客可以免费携带一定质量的行李,但超过该质量则需购买行李票,且行李费y(元)是行李质量x(kg)的一次函数,现知李明带了60kg的行李,交了行李费5元,王华带了90kg的行李,交了行李费10元.
(1)写出y与x之间的函数表达式
(2)旅客最多可免费携带多少千克的行李?
解:(1)设y=kx+b,根据题意,得
解得
所以 y与x之间的函数表达式为
(2)当y=0时,
解得x=30
所以旅客最多可以免
费携带30 kg的行李。
学习新知
2、利用待定系数法求一次函数表达式的主要步骤如下:
(1)设出函数表达式: y=kx+b;
(2)把已知条件代入,得到关于k、b的方程组;
(3)解方程组,求出k、b的值;
(4)写出其表达式.
知识升华
1、像本例这样,先设出函数表达式,再根据所给条件确定表达式中未知数的系数,从而得到函数表达式的方法,叫做待定系数法.
1.在弹性限度内,弹簧的长度y(cm)是所挂物体质量x(kg)的一次函数.当所挂物体的质量为1kg时,弹簧长15cm;当所挂物体的质量为3kg时,弹簧长16cm.写出y与x之间的关系式,并求当所挂物体的质量为4kg时弹簧的长度.
解:(1)设y=kx+b,根据题意,得
解得
∴y与x之间的函数表达式为
(2)当x=4时,
y=0.5×4+14.5
解得y=16.5
∴当所挂物体的质量
为4kg时弹簧的长为16.5cm.
五、课内训练(一)
2.图中的两条直线 , 的交点坐标是 ,
、
可以看作方程组 的解。
解:设直线 的解析式为 y=k1x+b1,
分别把( , )和( , )代入得
设直线 的解析式为 y=k2x+b2,
分别把( , )和( , )代入得
课内训练(二)——精英园地
2.图中的两条直线 , 的交点坐标是 ,
它可以看作方程组 的解。
解:设直线 的解析式为 y=k1x+b1,
分别把( 0 , 1 )和( 1 , 3 )代入得
解得
∴直线 的解析式为 y=2x+1
设直线 的解析式为 y=k2x+b2,
分别把( 0 , 4 )和( 1 , 3 )代入得
解得
∴直线 的解析式为 y=-x+4
∴这交点可以看成是
的解
七、课堂小结
谈谈本节课你的收获与感受
八、检测反馈
x -2 0 1
y 3 p 0
1.一次函数y=kx+b经过点(1,1),(2,- 4),则k与b的值为( )
2.根据下表中一次函数的自变量x与函数y的部分对应值,可得p的值为( )
A.1 B.-1 C.3 D.-3
3.已知函数y=2x+b的图象经过点(a, 7)和(-2,a),求这个函数表达式。
九、作业布置
A组:P128问题解决 1,2
B组:
已知点A(1,2)B(2,-3)C(3,-4),问A,B,C三点在同一直线吗?
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
