人教版八年级数学下册课件:19.2.1正比例函数(共19张PPT)
文档属性
| 名称 | 人教版八年级数学下册课件:19.2.1正比例函数(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 324.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-06 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
19.2 一次函数
第1课时 正比例函数
观察以下函数
这些函数有什么共同点?
这些函数都是常数与自变量的乘积的形式。
(2)T= -2t
(1)l=2πr
(3)h=0.5n
(4) s= 8.54t (0≤t ≤12.88)
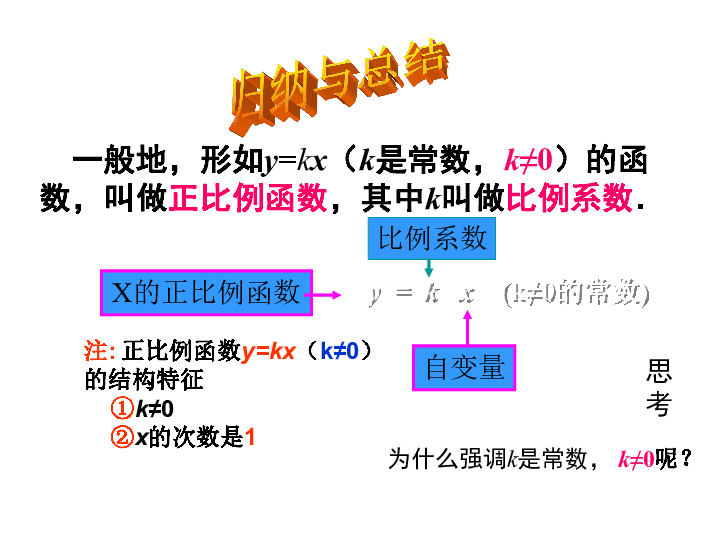
归纳与总结
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
思考
为什么强调k是常数, k≠0呢?
y = k x (k≠0的常数)
比例系数
自变量
X的正比例函数
注: 正比例函数y=kx(k≠0)
的结构特征
①k≠0
②x的次数是1
1.下列函数是否是正比例函数?比例系数是
多少?
是,比例系数k=8.
不是.
不是.
是,比例系数k= .
练一练
(5)y=2x-1
不是.
应用新知
例1 (1)若y=5x3m-2是正比例函数,m= 。
1
变式练习1、若y=(m-1)xm2是关于 x的正比例函数,则m=
2、已知一个正比例函数的比例系数是-5,则它的解析式为:( )
(-1)
y=-5x
(2)若y=(3m-2)x是正比例函数,则m____.
例2:画出下列正比例函数 的图象(1)y=2x (2) y=-2x
画图步骤:
1、列表;
2、描点;
3、连线。
y=2x 的图象为:
-6
-4
-2
0
2
4
6
x … -3 -2 -1 0 1 2 3 …
y … …
y=-2x 的图象为:
6
4
2
0
-2
-4
-6
x … -3 -2 -1 0 1 2 3 …
y … …
探索新知:比较两个函数图象的相同点与不同点
两图象都是经过原点的 ,
函数y=2x的图象从左向右 ,经过第 象限, y随x的增大而 ;
函数y=-2x的图象从左向右 ,经过第 象限,y随x的增大而 。
直线
上升
一、三
下降
二、四
k>0
k<0
增大
减小
看图 , 在同一坐标系下,观察下列函数的图象,并对它们进行比较:
(1) (2)
x
-5
-4
-3
-2
-1
5
4
3
2
1
-1 0
-2
-3
-4
-5
1
2
3
4
5
x
y
知识要点
正是由于正比例函数y=kx(k是常数,k≠ 0)的图象是一条直线,我们可以称它为直线y=kx.
y=kx (k是常数,k≠0)的图象是一条经过原点的直线
y=kx 经过的象限 从左向右 Y随x的增大而
k>0 第一、三象限 上升 增大
k<0 第二、四象限 下降 减小
B
1.下列图象哪个可能是函数y=-8x的图象( )
A B C D
应用新知
2.正比例函数图象y=(m-1)x的图像经过第一,三象限,则m的取值范围是( )。
A,m=1 B,m>1 C,m<1 D,m>=1
B
3、关于函数y=-2x,下列判断正确的是( )
A、图象必过点(-1,-2)
B、图象经过一、三象限
C、y随x增大而减小
D 、 不论x为何值都有y<0
4、在正比例函数y=4x中, y随x的增大而( )在正比例数 y=-6x中 , y随x的增大( )。
5、任意写一个图象经过二、四象限的正比例函数的解析式为( )。
C
增大
减小
Y=-3x
感悟与收获
经过本节课的学
习,你有哪些收获?
请和我们一起分享。
试一试
同桌两人一组,一人写出一个正比例函数解析式。
另一人:说出这个函数的图象特征。
思 考
?
若点 (-1,a),(2,b)都在直线y=4x上,试比较a,b的大小
还有其他方法吗?
若y=kx(k<0)呢?
作业
今天作业是:
练习题;
1.下列函数关系中,为正比例函数的是( ).
A.圆的面积S和它的半径r
B.路程为常数s时,行走的速度v与时间t
C.被除数是常数a时,除数b与商c
D.三角形的底边长是常数a时,其面积S与底
边上的高h
2.若函数y=(m-1)xm2是正比例函数,则m的值
为( ).
A.±1 B.1 C.-1 D.不存在
D
C
随堂练习
19.2 一次函数
第1课时 正比例函数
观察以下函数
这些函数有什么共同点?
这些函数都是常数与自变量的乘积的形式。
(2)T= -2t
(1)l=2πr
(3)h=0.5n
(4) s= 8.54t (0≤t ≤12.88)
归纳与总结
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
思考
为什么强调k是常数, k≠0呢?
y = k x (k≠0的常数)
比例系数
自变量
X的正比例函数
注: 正比例函数y=kx(k≠0)
的结构特征
①k≠0
②x的次数是1
1.下列函数是否是正比例函数?比例系数是
多少?
是,比例系数k=8.
不是.
不是.
是,比例系数k= .
练一练
(5)y=2x-1
不是.
应用新知
例1 (1)若y=5x3m-2是正比例函数,m= 。
1
变式练习1、若y=(m-1)xm2是关于 x的正比例函数,则m=
2、已知一个正比例函数的比例系数是-5,则它的解析式为:( )
(-1)
y=-5x
(2)若y=(3m-2)x是正比例函数,则m____.
例2:画出下列正比例函数 的图象(1)y=2x (2) y=-2x
画图步骤:
1、列表;
2、描点;
3、连线。
y=2x 的图象为:
-6
-4
-2
0
2
4
6
x … -3 -2 -1 0 1 2 3 …
y … …
y=-2x 的图象为:
6
4
2
0
-2
-4
-6
x … -3 -2 -1 0 1 2 3 …
y … …
探索新知:比较两个函数图象的相同点与不同点
两图象都是经过原点的 ,
函数y=2x的图象从左向右 ,经过第 象限, y随x的增大而 ;
函数y=-2x的图象从左向右 ,经过第 象限,y随x的增大而 。
直线
上升
一、三
下降
二、四
k>0
k<0
增大
减小
看图 , 在同一坐标系下,观察下列函数的图象,并对它们进行比较:
(1) (2)
x
-5
-4
-3
-2
-1
5
4
3
2
1
-1 0
-2
-3
-4
-5
1
2
3
4
5
x
y
知识要点
正是由于正比例函数y=kx(k是常数,k≠ 0)的图象是一条直线,我们可以称它为直线y=kx.
y=kx (k是常数,k≠0)的图象是一条经过原点的直线
y=kx 经过的象限 从左向右 Y随x的增大而
k>0 第一、三象限 上升 增大
k<0 第二、四象限 下降 减小
B
1.下列图象哪个可能是函数y=-8x的图象( )
A B C D
应用新知
2.正比例函数图象y=(m-1)x的图像经过第一,三象限,则m的取值范围是( )。
A,m=1 B,m>1 C,m<1 D,m>=1
B
3、关于函数y=-2x,下列判断正确的是( )
A、图象必过点(-1,-2)
B、图象经过一、三象限
C、y随x增大而减小
D 、 不论x为何值都有y<0
4、在正比例函数y=4x中, y随x的增大而( )在正比例数 y=-6x中 , y随x的增大( )。
5、任意写一个图象经过二、四象限的正比例函数的解析式为( )。
C
增大
减小
Y=-3x
感悟与收获
经过本节课的学
习,你有哪些收获?
请和我们一起分享。
试一试
同桌两人一组,一人写出一个正比例函数解析式。
另一人:说出这个函数的图象特征。
思 考
?
若点 (-1,a),(2,b)都在直线y=4x上,试比较a,b的大小
还有其他方法吗?
若y=kx(k<0)呢?
作业
今天作业是:
练习题;
1.下列函数关系中,为正比例函数的是( ).
A.圆的面积S和它的半径r
B.路程为常数s时,行走的速度v与时间t
C.被除数是常数a时,除数b与商c
D.三角形的底边长是常数a时,其面积S与底
边上的高h
2.若函数y=(m-1)xm2是正比例函数,则m的值
为( ).
A.±1 B.1 C.-1 D.不存在
D
C
随堂练习
