北师大版高中数学必修五第三章第4节《二元一次不等式(组)与平面区域》第一课时(共15张PPT)
文档属性
| 名称 | 北师大版高中数学必修五第三章第4节《二元一次不等式(组)与平面区域》第一课时(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-07 20:18:56 | ||
图片预览





文档简介
(共15张PPT)
北师大版 高中数学 必修五
第三章 简单线性规划
§4.1 二元一次不等式(组)与平面区域
(第一课时)
江西省2020年寒假及春季学期延期开学期间
线上教育课程
某年一名刚参加工作的大学生为自己制定的每月用餐费的最低标准是240元,又知其他费用最少需支出180元,而每月可用来支配的资金为500元,这名新员工可以如何使用这些钱?
设用餐费为元,其他费用为元,由题意不小于240,不小于180,与之和不超过500,用不等式组可表示为:
在平面直角坐标系中,表示一条直线,它将直角坐标系分成三部分,即自身和它的两侧.在直线上任意一点的坐标都满足.
讨论:平面直角坐标系中哪些点满足不等式.
1
-1
在直线上任取一点,例如,取点,过这点作与轴平行的直线.
上所有点的横坐标都是1,在上,取的下侧一点,显然它的横坐标大于纵坐标,满足不等式.
不难看出,在上,点下侧的任意一点的坐标都满足不等式.
同样地,在直线上方的任意一点的坐标都满足不等式.
由于可在直线上任取,所以在直线下方的任意一点的坐标都满足不等式.
(2)
1
(1)
1
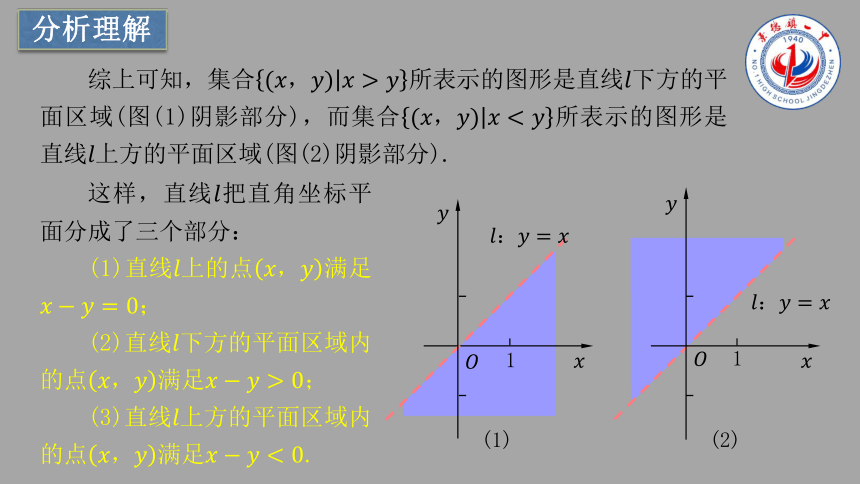
综上可知,集合所表示的图形是直线下方的平面区域(图(1)阴影部分),而集合所表示的图形是直线上方的平面区域(图(2)阴影部分).
这样,直线把直角坐标平面分成了三个部分:
(1)直线上的点满足;
(2)直线下方的平面区域内的点满足;
(3)直线上方的平面区域内的点满足.
例1 试确定集合表示的平面区域.
解 直线将直角坐标平面分成三部分(及其两侧).在上方的平面区域内的任一点的坐标满足不等式,而另外两部分的点均不满足不等式.不等式表示的是直线上方的平面区域(图中的阴影部分).
1
分析 作直线,把直角坐标平面分成三部分.在上取一点,过这点作一条与轴平行的直线,
在上点的下侧取任意一点,它的纵坐标,于是,即点的坐标满足不等式.
同理,在上取一点,过作轴的平行线,可以说明:在上,点上侧任意一点的坐标都满足不等式;点下侧任意一点的坐标都满足不等式.
在上点的上侧取任意一点,它的纵坐标,于是,即点的坐标满足不等式;
一般地,直线把直角坐标平面分成了三个
部分:
(1)直线上的点的坐标满足;
(2)直线一侧的平面区域内的点的坐标满足;
(3)直线另一侧的平面区域内的点的坐标满足.
所以,只需在直线的某一侧的平面区域内,任取一特殊点,从值的正负,即可判断不等式表示的平面区域.
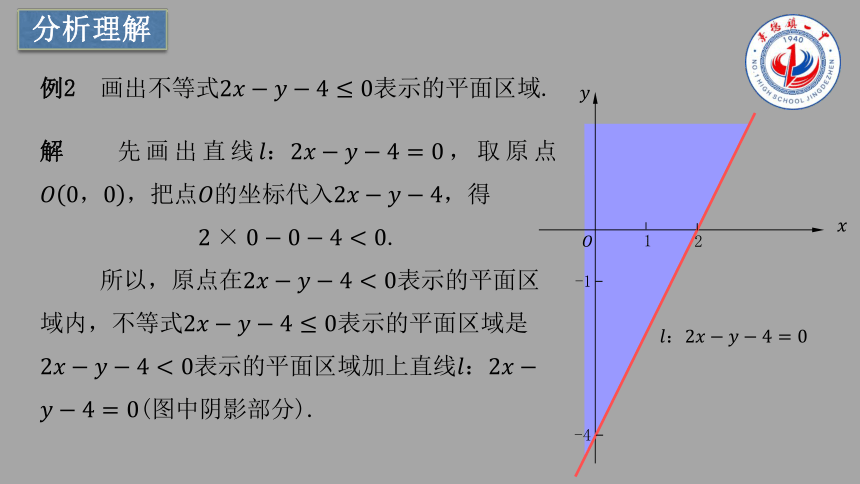
例2 画出不等式表示的平面区域.
解 先画出直线,取原点,把点的坐标代入,得
.
所以,原点在表示的平面区域内,不等式表示的平面区域是表示的平面区域加上直线(图中阴影部分).
1
2
-4
-1
例3 画出以下不等式组表示的平面区域.
1
1
分析 不等式组表示的平面区域是不等式,,所表示的平面区域的公共部分.
解 如图所示.
不等式表示直线的上方(包括直线)的平面区域;
不等式表示直线下方(包括直线)的平面区域;
不等式表示直线左方(包括直线)的平面区域.
所以,原不等式组表示上述平面区域的公共部分(阴影部分).
1. 图中表示的平面区域满足不等式( ).
A. B.
C. D.
1
(第1题)
1
B
7
2
1
1
2. 画出不等式表示的平面区域.
1
1
3. 画出不等式组表示的平面区域.
1. 理解二元一次不等式的解集是直线分直角坐标系平面区域的某
侧区域,体会到数形结合思想在表示二元一次不等式解集中的应用;
2. 判定二元一次不等式表示的平面区域的方法:
以线定界,以点(原点)定域(以为例).
(1)“以线定界”,即画二元一次方程表示的直线定边界,其中要注意实线或虚线;
(2)“以点定域”,由于对在直线同侧的点,实数的值的符号都相同,故为了确定的符号,可采用取特殊点法,如取原点等.
3. 掌握二元一次不等式组的解集是取多个不等式所表示区域的公
共部分,具体步骤如下:
(1)画线——画出不等式所反应的方程表示的直线(如果原不等式中带等号,则画成实线,否则画成虚线);
(2)定侧——将某个区域位置明显的特殊点的坐标代入不等式,根据“同侧同号、异侧异号”的规律确定不等式所表示的平面区域在直线的哪一侧;
(3)求“交”——如果平面区域是由不等式组决定的,则在确定了各个不等式所表示的区域后,再求这些区域的公共部分,这个公共部分就是不等式组表示的平面区域.
课本 P108 习题 3-4
A 组 第1、2题
同 学 们 再 见 !
北师大版 高中数学 必修五
第三章 简单线性规划
§4.1 二元一次不等式(组)与平面区域
(第一课时)
江西省2020年寒假及春季学期延期开学期间
线上教育课程
某年一名刚参加工作的大学生为自己制定的每月用餐费的最低标准是240元,又知其他费用最少需支出180元,而每月可用来支配的资金为500元,这名新员工可以如何使用这些钱?
设用餐费为元,其他费用为元,由题意不小于240,不小于180,与之和不超过500,用不等式组可表示为:
在平面直角坐标系中,表示一条直线,它将直角坐标系分成三部分,即自身和它的两侧.在直线上任意一点的坐标都满足.
讨论:平面直角坐标系中哪些点满足不等式.
1
-1
在直线上任取一点,例如,取点,过这点作与轴平行的直线.
上所有点的横坐标都是1,在上,取的下侧一点,显然它的横坐标大于纵坐标,满足不等式.
不难看出,在上,点下侧的任意一点的坐标都满足不等式.
同样地,在直线上方的任意一点的坐标都满足不等式.
由于可在直线上任取,所以在直线下方的任意一点的坐标都满足不等式.
(2)
1
(1)
1
综上可知,集合所表示的图形是直线下方的平面区域(图(1)阴影部分),而集合所表示的图形是直线上方的平面区域(图(2)阴影部分).
这样,直线把直角坐标平面分成了三个部分:
(1)直线上的点满足;
(2)直线下方的平面区域内的点满足;
(3)直线上方的平面区域内的点满足.
例1 试确定集合表示的平面区域.
解 直线将直角坐标平面分成三部分(及其两侧).在上方的平面区域内的任一点的坐标满足不等式,而另外两部分的点均不满足不等式.不等式表示的是直线上方的平面区域(图中的阴影部分).
1
分析 作直线,把直角坐标平面分成三部分.在上取一点,过这点作一条与轴平行的直线,
在上点的下侧取任意一点,它的纵坐标,于是,即点的坐标满足不等式.
同理,在上取一点,过作轴的平行线,可以说明:在上,点上侧任意一点的坐标都满足不等式;点下侧任意一点的坐标都满足不等式.
在上点的上侧取任意一点,它的纵坐标,于是,即点的坐标满足不等式;
一般地,直线把直角坐标平面分成了三个
部分:
(1)直线上的点的坐标满足;
(2)直线一侧的平面区域内的点的坐标满足;
(3)直线另一侧的平面区域内的点的坐标满足.
所以,只需在直线的某一侧的平面区域内,任取一特殊点,从值的正负,即可判断不等式表示的平面区域.
例2 画出不等式表示的平面区域.
解 先画出直线,取原点,把点的坐标代入,得
.
所以,原点在表示的平面区域内,不等式表示的平面区域是表示的平面区域加上直线(图中阴影部分).
1
2
-4
-1
例3 画出以下不等式组表示的平面区域.
1
1
分析 不等式组表示的平面区域是不等式,,所表示的平面区域的公共部分.
解 如图所示.
不等式表示直线的上方(包括直线)的平面区域;
不等式表示直线下方(包括直线)的平面区域;
不等式表示直线左方(包括直线)的平面区域.
所以,原不等式组表示上述平面区域的公共部分(阴影部分).
1. 图中表示的平面区域满足不等式( ).
A. B.
C. D.
1
(第1题)
1
B
7
2
1
1
2. 画出不等式表示的平面区域.
1
1
3. 画出不等式组表示的平面区域.
1. 理解二元一次不等式的解集是直线分直角坐标系平面区域的某
侧区域,体会到数形结合思想在表示二元一次不等式解集中的应用;
2. 判定二元一次不等式表示的平面区域的方法:
以线定界,以点(原点)定域(以为例).
(1)“以线定界”,即画二元一次方程表示的直线定边界,其中要注意实线或虚线;
(2)“以点定域”,由于对在直线同侧的点,实数的值的符号都相同,故为了确定的符号,可采用取特殊点法,如取原点等.
3. 掌握二元一次不等式组的解集是取多个不等式所表示区域的公
共部分,具体步骤如下:
(1)画线——画出不等式所反应的方程表示的直线(如果原不等式中带等号,则画成实线,否则画成虚线);
(2)定侧——将某个区域位置明显的特殊点的坐标代入不等式,根据“同侧同号、异侧异号”的规律确定不等式所表示的平面区域在直线的哪一侧;
(3)求“交”——如果平面区域是由不等式组决定的,则在确定了各个不等式所表示的区域后,再求这些区域的公共部分,这个公共部分就是不等式组表示的平面区域.
课本 P108 习题 3-4
A 组 第1、2题
同 学 们 再 见 !
