北师大版高中数学选修1-1第4章第2节《导数在实际问题中的应用》课件(共26张PPT)
文档属性
| 名称 | 北师大版高中数学选修1-1第4章第2节《导数在实际问题中的应用》课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-06 00:00:00 | ||
图片预览



文档简介
(共24张PPT)
实际问题中导数的意义
北师大版-高中数学选修1-1第4章 导数应用
第2节 导数在实际问题中的应用
赣
课题引入 导数来源生活
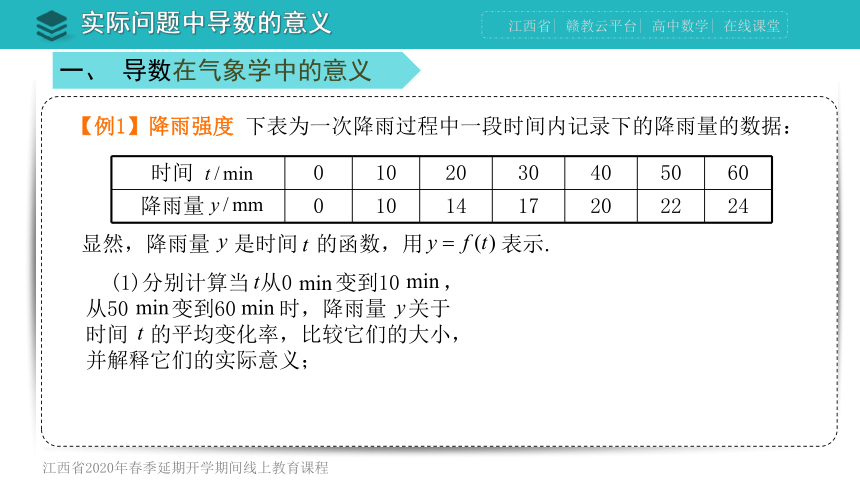
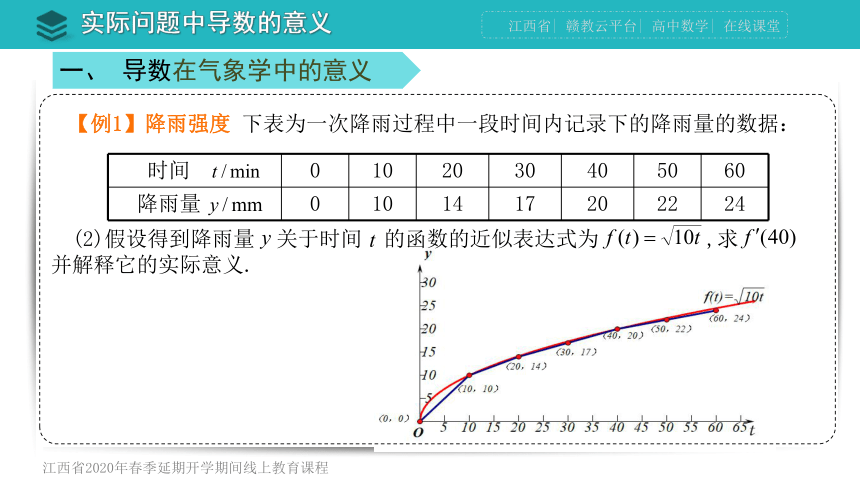
【例1】降雨强度 下表为一次降雨过程中一段时间内记录下的降雨量的数据:
一、 导数在气象学中的意义
时间 0 10 20 30 40 50 60
降雨量 0 10 14 17 20 22 24
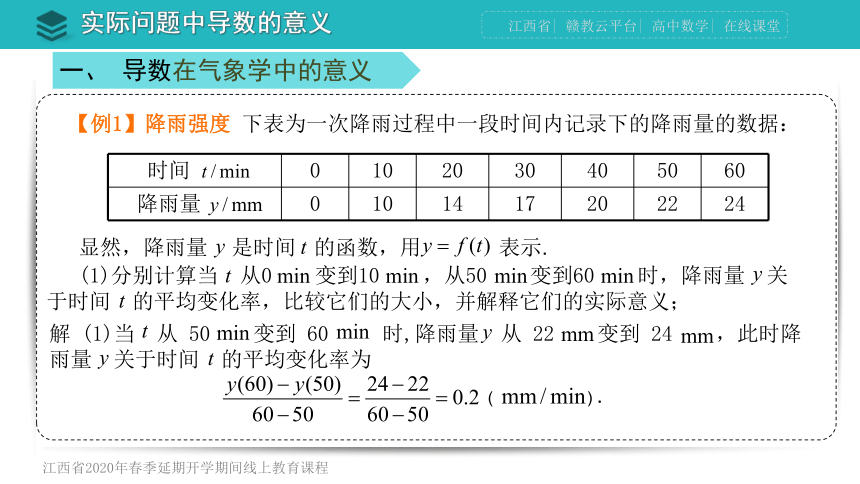
【例1】降雨强度 下表为一次降雨过程中一段时间内记录下的降雨量的数据:
一、 导数在气象学中的意义
时间 0 10 20 30 40 50 60
降雨量 0 10 14 17 20 22 24
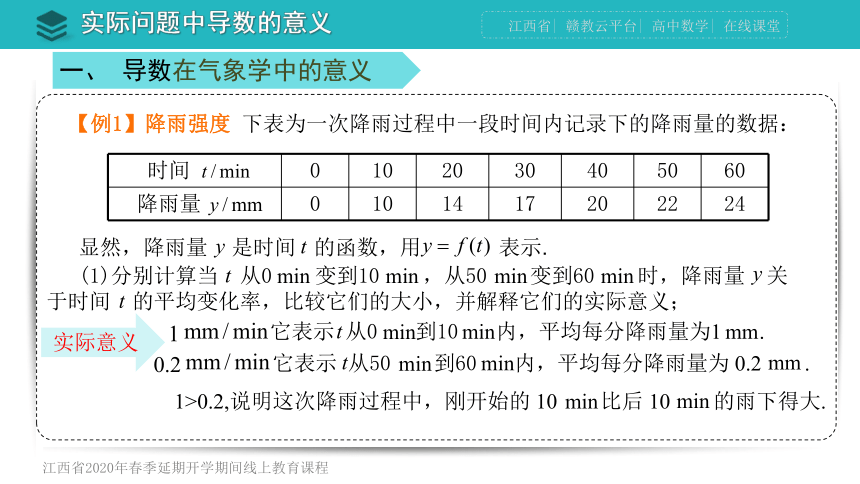
【例1】降雨强度 下表为一次降雨过程中一段时间内记录下的降雨量的数据:
一、 导数在气象学中的意义
时间 0 10 20 30 40 50 60
降雨量 0 10 14 17 20 22 24
【例1】降雨强度 下表为一次降雨过程中一段时间内记录下的降雨量的数据:
显然,降雨量 是时间 的函数,用 表示.
一、 导数在气象学中的意义
时间 0 10 20 30 40 50 60
降雨量 0 10 14 17 20 22 24
【例1】降雨强度 下表为一次降雨过程中一段时间内记录下的降雨量的数据:
一、 导数在气象学中的意义
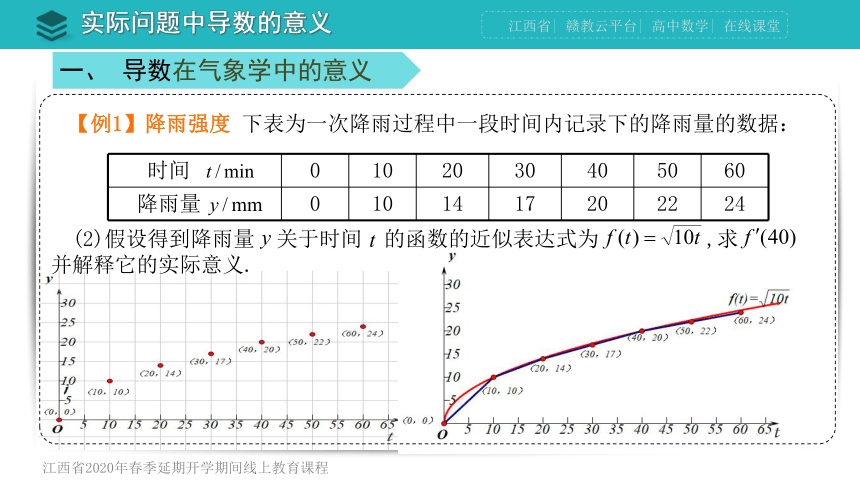
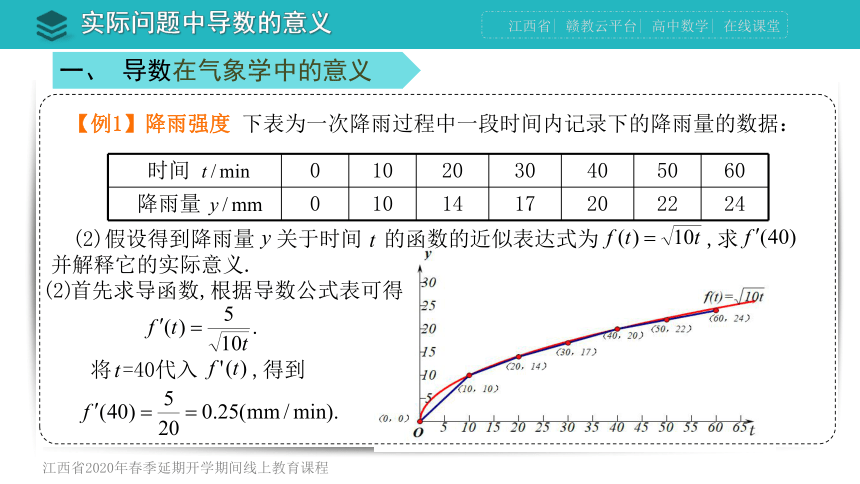
(2)假设得到降雨量 关于时间 的函数的近似表达式为 ,求 并解释它的实际意义.
时间 0 10 20 30 40 50 60
降雨量 0 10 14 17 20 22 24
【例1】降雨强度 下表为一次降雨过程中一段时间内记录下的降雨量的数据:
(2)假设得到降雨量 关于时间 的函数的近似表达式为 ,求 并解释它的实际意义.
一、 导数在气象学中的意义
时间 0 10 20 30 40 50 60
降雨量 0 10 14 17 20 22 24
【例1】降雨强度 下表为一次降雨过程中一段时间内记录下的降雨量的数据:
(2)假设得到降雨量 关于时间 的函数的近似表达式为 ,求 并解释它的实际意义.
一、 导数在气象学中的意义
(2)
首先求导函数,根据导数公式表可得
时间 0 10 20 30 40 50 60
降雨量 0 10 14 17 20 22 24
(2)假设得到降雨量 关于时间 的函数的近似表达式为 ,求 并解释它的实际意义.
【例1】降雨强度 下表为一次降雨过程中一段时间内记录下的降雨量的数据:
它表示的是 时降雨量 关于时间 的瞬时变化率,
即降雨强度.
一、 导数在气象学中的意义
时间 0 10 20 30 40 50 60
降雨量 0 10 14 17 20 22 24
【例1】降雨强度 下表为一次降雨过程中一段时间内记录下的降雨量的数据:
(2)假设得到降雨量 关于时间 的函数的近似表达式为 ,求 并解释它的实际意义.
.
一、 导数在气象学中的意义
时间 0 10 20 30 40 50 60
降雨量 0 10 14 17 20 22 24
二、 导数在物理学中的意义
【思路分析】
如图所示,某人拉动一个物体前进,
二、 导数在物理学中的意义
.
二、 导数在物理学中的意义
(2)求 , ,并解释他们的实际意义.
,
在物理学中,通常称力在单位时间内做的功为功率,它的单位是瓦特.
三、导数在经济学中的意义
表示当建筑面积从100 增加到120 的过程中每增加1 的建筑面积,建筑成本平均约增加1050元.
三、 导数在经济学中的意义
.
(2)求导得
三、 导数在经济学中的意义
表示当建筑面积为100 时,
成本增加的速度为 1050 元/ ,
通过研究学生的学习行为,心理学家发现接受能力(即学生掌握一个概念的能力)依赖于在概念引入之前老师提出和描述问题所用的时间. 讲授开始时,学生的兴趣激增,但随着时间的延长,学生的注意力开始分散.分析结果表明,一些学生掌握概念的能力由下式给出:
练习巩固 导数服务生活
【练习】
解
,
练习巩固 导数服务生活
(2) 第 10? 时,学生的学习能力是在增加还是降低?
,
通过研究学生的学习行为,心理学家发现接受能力(即学生掌握一个概念的能力)依赖于在概念引入之前老师提出和描述问题所用的时间. 讲授开始时,学生的兴趣激增,但随着时间的延长,学生的注意力开始分散.分析结果表明,一些学生掌握概念的能力由下式给出:
【练习】
练习巩固 导数服务生活
导数大于 0 ,函数是增加的,说明第 10 时学生的学习能力在增加.
解 (2)
,
通过研究学生的学习行为,心理学家发现接受能力(即学生掌握一个概念的能力)依赖于在概念引入之前老师提出和描述问题所用的时间. 讲授开始时,学生的兴趣激增,但随着时间的延长,学生的注意力开始分散.分析结果表明,一些学生掌握概念的能力由下式给出:
【练习】
课堂小结
一、导数在实际生活和科学研究中有着非常广泛的应用
二、实际问题中导数意义的解释方法
1.瞬时性解释
2.特定意义解释
瞬时变化率
降雨强度
功率
边际成本
一个单位的平均变化率
导数
导数
课后作业
( 2 )求 , ,并解释它们的实际意义 .
( 1 ) 求当 从 2 变到4 ,该工人生产的产品量 关于时间 的平均变化率,并解释它们的实际意义;
( 2 ) 求 ,并解释它们的实际意义.
2.一名工人的研究表明,工作 后生产出的产品量 (单位: )可以近似表示为
1.一个电路中,流过的电荷量 (单位: )关于时间 (单位: )的函数为
.
,
17.67,它的实际意义是在 = 3 这一时刻,每秒经过该电路的电量约为 17.76 ,也就是这段时间内电路的电流约为 17.67 .
课后作业参考解答
1.(1)平均变化率为 8.31,它表示在 =1 到 = 2 这段时间内平均每秒经过该电路的电量为 8.31 也就是这段时间内电路的平均电流为8.31 ;
(2)
谢谢
THANKS
实际问题中导数的意义
北师大版-高中数学选修1-1第4章 导数应用
第2节 导数在实际问题中的应用
赣
课题引入 导数来源生活
【例1】降雨强度 下表为一次降雨过程中一段时间内记录下的降雨量的数据:
一、 导数在气象学中的意义
时间 0 10 20 30 40 50 60
降雨量 0 10 14 17 20 22 24
【例1】降雨强度 下表为一次降雨过程中一段时间内记录下的降雨量的数据:
一、 导数在气象学中的意义
时间 0 10 20 30 40 50 60
降雨量 0 10 14 17 20 22 24
【例1】降雨强度 下表为一次降雨过程中一段时间内记录下的降雨量的数据:
一、 导数在气象学中的意义
时间 0 10 20 30 40 50 60
降雨量 0 10 14 17 20 22 24
【例1】降雨强度 下表为一次降雨过程中一段时间内记录下的降雨量的数据:
显然,降雨量 是时间 的函数,用 表示.
一、 导数在气象学中的意义
时间 0 10 20 30 40 50 60
降雨量 0 10 14 17 20 22 24
【例1】降雨强度 下表为一次降雨过程中一段时间内记录下的降雨量的数据:
一、 导数在气象学中的意义
(2)假设得到降雨量 关于时间 的函数的近似表达式为 ,求 并解释它的实际意义.
时间 0 10 20 30 40 50 60
降雨量 0 10 14 17 20 22 24
【例1】降雨强度 下表为一次降雨过程中一段时间内记录下的降雨量的数据:
(2)假设得到降雨量 关于时间 的函数的近似表达式为 ,求 并解释它的实际意义.
一、 导数在气象学中的意义
时间 0 10 20 30 40 50 60
降雨量 0 10 14 17 20 22 24
【例1】降雨强度 下表为一次降雨过程中一段时间内记录下的降雨量的数据:
(2)假设得到降雨量 关于时间 的函数的近似表达式为 ,求 并解释它的实际意义.
一、 导数在气象学中的意义
(2)
首先求导函数,根据导数公式表可得
时间 0 10 20 30 40 50 60
降雨量 0 10 14 17 20 22 24
(2)假设得到降雨量 关于时间 的函数的近似表达式为 ,求 并解释它的实际意义.
【例1】降雨强度 下表为一次降雨过程中一段时间内记录下的降雨量的数据:
它表示的是 时降雨量 关于时间 的瞬时变化率,
即降雨强度.
一、 导数在气象学中的意义
时间 0 10 20 30 40 50 60
降雨量 0 10 14 17 20 22 24
【例1】降雨强度 下表为一次降雨过程中一段时间内记录下的降雨量的数据:
(2)假设得到降雨量 关于时间 的函数的近似表达式为 ,求 并解释它的实际意义.
.
一、 导数在气象学中的意义
时间 0 10 20 30 40 50 60
降雨量 0 10 14 17 20 22 24
二、 导数在物理学中的意义
【思路分析】
如图所示,某人拉动一个物体前进,
二、 导数在物理学中的意义
.
二、 导数在物理学中的意义
(2)求 , ,并解释他们的实际意义.
,
在物理学中,通常称力在单位时间内做的功为功率,它的单位是瓦特.
三、导数在经济学中的意义
表示当建筑面积从100 增加到120 的过程中每增加1 的建筑面积,建筑成本平均约增加1050元.
三、 导数在经济学中的意义
.
(2)求导得
三、 导数在经济学中的意义
表示当建筑面积为100 时,
成本增加的速度为 1050 元/ ,
通过研究学生的学习行为,心理学家发现接受能力(即学生掌握一个概念的能力)依赖于在概念引入之前老师提出和描述问题所用的时间. 讲授开始时,学生的兴趣激增,但随着时间的延长,学生的注意力开始分散.分析结果表明,一些学生掌握概念的能力由下式给出:
练习巩固 导数服务生活
【练习】
解
,
练习巩固 导数服务生活
(2) 第 10? 时,学生的学习能力是在增加还是降低?
,
通过研究学生的学习行为,心理学家发现接受能力(即学生掌握一个概念的能力)依赖于在概念引入之前老师提出和描述问题所用的时间. 讲授开始时,学生的兴趣激增,但随着时间的延长,学生的注意力开始分散.分析结果表明,一些学生掌握概念的能力由下式给出:
【练习】
练习巩固 导数服务生活
导数大于 0 ,函数是增加的,说明第 10 时学生的学习能力在增加.
解 (2)
,
通过研究学生的学习行为,心理学家发现接受能力(即学生掌握一个概念的能力)依赖于在概念引入之前老师提出和描述问题所用的时间. 讲授开始时,学生的兴趣激增,但随着时间的延长,学生的注意力开始分散.分析结果表明,一些学生掌握概念的能力由下式给出:
【练习】
课堂小结
一、导数在实际生活和科学研究中有着非常广泛的应用
二、实际问题中导数意义的解释方法
1.瞬时性解释
2.特定意义解释
瞬时变化率
降雨强度
功率
边际成本
一个单位的平均变化率
导数
导数
课后作业
( 2 )求 , ,并解释它们的实际意义 .
( 1 ) 求当 从 2 变到4 ,该工人生产的产品量 关于时间 的平均变化率,并解释它们的实际意义;
( 2 ) 求 ,并解释它们的实际意义.
2.一名工人的研究表明,工作 后生产出的产品量 (单位: )可以近似表示为
1.一个电路中,流过的电荷量 (单位: )关于时间 (单位: )的函数为
.
,
17.67,它的实际意义是在 = 3 这一时刻,每秒经过该电路的电量约为 17.76 ,也就是这段时间内电路的电流约为 17.67 .
课后作业参考解答
1.(1)平均变化率为 8.31,它表示在 =1 到 = 2 这段时间内平均每秒经过该电路的电量为 8.31 也就是这段时间内电路的平均电流为8.31 ;
(2)
谢谢
THANKS
同课章节目录
